1 − 2 + 3 − 4 + …

在数学中，1 − 2 + 3 − 4 + …表示以由小到大的接续正整數，依次加後又減、減後又加，如此反复所構成的無窮級數。它是交錯級數，若以Σ符号表示前m项之和，可写作：

${\displaystyle \sum _{n=1}^{m}n(-1)^{n-1}}$

1 − 2 + 3 − 4 + …的前一萬五千项相加结果示意图

此无穷级数发散，即其部分和的序列（1, −1, 2, −2, …）不会趋近于任一有穷极限。也就是說，單從極限的角度看的話，1 − 2 + 3 − 4 + …不存在和。不过，在18世纪中期，莱昂哈德·欧拉写出了一个他承认为悖论的等式：

${\displaystyle 1-2+3-4+\cdots ={\frac {1}{4}}}$

该等式的严谨解释在很久以后才出现。自1890年起，恩纳斯托·切萨罗、埃米尔·博雷尔与其他一些数学家就在研究有哪些定义良好的方法，可以给发散级数賦予广义和^{[註 1]}——其中包含了对欧拉结果的新解释。这些求和法大部分可简单地指定1 − 2 + 3 − 4 + …的“和”為¹⁄₄。切萨罗求和是少数几种不能计算出1 − 2 + 3 − 4 + …之和的方法，因为此级数求和需要某个略强的方法——譬如阿贝耳求和。

级数1 − 2 + 3 − 4 + …与格蘭迪級數1 − 1 + 1 − 1 + …有紧密的联系。欧拉将这两个级数当作1 − 2ⁿ + 3ⁿ − 4ⁿ + …的特例（其中n为任意自然数），这个级数既直接扩展了他在巴塞尔问题上所做的工作，同时也引出了我们现在所知的狄利克雷η函数和黎曼ζ函数。

发散性

级数项（1, −2, 3, −4, …）不趋近于0，因此通过项测试便可确定1 − 2 + 3 − 4 + …发散。不過作为后文的参考，此處也以基礎的方法去證明此級數發散。首先，从定义可知，无穷级数的敛散性是由其部分和的敛散性所确定的，1 − 2 + 3 − 4 + …的部分和为：^[1]

1 = 1,

1 − 2 = −1,

1 − 2 + 3 = 2,

1 − 2 + 3 − 4 = −2,

1 − 2 + 3 − 4 + 5 = 3,

1 − 2 + 3 − 4 + 5 − 6 = −3,

…

此部分和序列的一个显著特点是每个整数都恰好出现一次——如果将空部分和计入还包括0——因此它還說明了整数集${\displaystyle \mathbb {Z} }$是可数的。^[2]很明显的，不可能让变化的结果收斂到一个确定的数^{[註 2]}，因此1 − 2 + 3 − 4 + …发散。

求和的启发

稳定性与线性

由于各项 1, −2, 3, −4, 5, −6, … 以一种简单模式排列，级数1 − 2 + 3 − 4 + …可以透過移項以及逐项求和，再透過解方程得出一数值。暂时假设s = 1 − 2 + 3 − 4 + …這樣的寫法有意义——其中的s为常数，那麼以下的計算將說明s = ¹⁄₄：

${\displaystyle {\begin{smallmatrix}4s&=&\!&(\,1\,-\,2\,+\,3\,-\,4\,+\,\cdots )&+\ \ \;\;\,&(\,1\,-\,2\,+\,3\,-\,4\,+\,\cdots )&+\ \ \;\;\,&(\,1\,-\,2\,+\,3\,-\,4\,+\,\cdots )&+\ \ \;\;\,&(\,1\,-\,2\,+\,3\,-\,4\,+\,\cdots )\quad \,\\\\\ &=&\!&({\color {Blue}\,1\,-\,2\,+\,3\,-\,4\,+\,\cdots })&+\,1\,+&({\color {Red}\,-\,2\,+\,3\,-\,4\,+\,5\,\cdots })&+\,1\,+&({\color {Purple}\,-\,2\,+\,3\,-\,4\,+\,5\,\cdots })&-\,1\,+&({\color {OliveGreen}\,3\,-\,4\,+\,5\,-\,6\,+\,\cdots })\quad \,\\\\\ &=&\ 1\,+&[\,(\,{\color {Blue}1}\,{\color {Red}-\,2}\,{\color {Purple}-\,2}\,{\color {OliveGreen}+\,3}\,)\quad &+\ \ \;\;\,&(\,{-\,\color {Blue}2}\,{\color {Red}+\,3}\,{\color {Purple}+\,3}\,{\color {OliveGreen}-\,4}\,)\;\;\;\,&+\ \ \;\;\,&(\,{\color {Blue}3}\,{\color {Red}-\,4}\,{\color {Purple}-\,4}\,{\color {OliveGreen}+\,5}\,)\ \quad &+\ \ \;\;\,&(\,{\color {Blue}-\,4}\,{\color {Red}+\,5}\,{\color {Purple}+\,5}\,{\color {OliveGreen}-\,6}\,)\,+\,\cdots ]\\\\\ &=&\ 1\,+&[\,0\,+\,0\,+\,0\,+\,0\,\cdots ]\ \;\\4s\ &=&\ 1\ \,\;\end{smallmatrix}}}$

因此，s = ¹⁄₄^[3]，如右图所示。

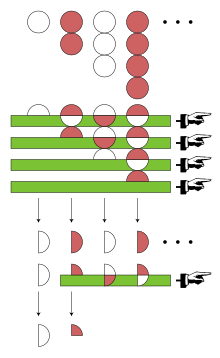
白球代表+1，紅球代表-1；把白球和紅球連起來，即是代表它們正負相消並等於0。如圖所示，复制4份1 − 2 + 3 − 4 + …，仅使用移项与逐项相加，结果为1。而單看左或右其中一邊的話，則是两个1 − 2 + 3 − 4 + …副本加起來，經抵消后得出1 − 1 + 1 − 1 + …。

尽管1 − 2 + 3 − 4 + …没有通常意义的和，等式s = 1 − 2 + 3 − 4 + … = ¹⁄₄却可被赋予另外一种意义。發散级数之“和”的一种普遍定义被称为一种求和法或可和法——通常是對於符合特定條件的一類級數可求和。求和法有许多种（部分将在下文中有所描述），这些方法跟普通求和也許有着一些共同的特性，例如：

1. 線性：設A^Σ為一種級數求和法。如果對於A^Σ可定義其上的那些序列，A^Σ是個線性泛函的話，則簡單地稱A^Σ是線性的。也就是說，對於序列r, s和純量k，有A^Σ(k r+s)=k A^Σ(r)+A^Σ(s)。
2. 穩定性：如果a是一個初項為a₀的序列，設a^*為a去掉初項後的序列，即對於一切n有a^*_n=a_n+1，那麼A^Σ(a)有定義当且仅当A^Σ(a^*)有定義。而且，A^Σ(a)=a₀ + A^Σ(a^*)。

因此，以上的計算实际上證明的是下面的內容：给出任意的线性且稳定的可和法，并能對级数1 − 2 + 3 − 4 + …求和，則结果必为¹⁄₄。此外，由于：

${\displaystyle {\begin{smallmatrix}2s&=&\!&(\,1\,-\,2\,+\,3\,-\,4\,+\,\cdots )\;\;\;&+\quad \quad \ &(\,1\,-\,2\,+\,3\,-\,4\,+\,\cdots )\quad \;\;\;\;\;\\\\\ &=&1\,+&(\,-\,2\,+\,3\,-\,4\,+\,\cdots )\quad \,&+\,1\,-\,2\,+&(\,3\,-\,4\,+\,5\,-\,\cdots )\qquad \ \;\;\;\;\,\\\\\ &=&0\,+&(\,(\,-\,2\,+\,3\,)\,+\,(\,3\,-\,4\,)&+\quad \quad \ &(\,-\,4\,+\,5\,)\,+\,(\,5\,-\,6\,)\,+\,\cdots )\\\\{\frac {1}{2}}&=&\!&\ \ \ 1\,\quad -\quad 1&+\quad \quad \ &\ \;1\quad -\quad 1\quad \cdots \end{smallmatrix}}}$

故此方法也一定能对格兰迪级数求和，并得结果为${\displaystyle 1-1+1-1+\cdots ={\begin{matrix}{\frac {1}{2}}\end{matrix}}}$

柯西乘积

1891年，恩纳斯托·切萨罗在他的一篇論文中指出有可能将发散级数严謹地納入微积分学，并寫道：

已可写出

${\displaystyle (1-1+1-1+\cdots )^{2}=1-2+3-4+\cdots }$

并断定两边均等於¹⁄₄。^[4]

对切萨罗而言，这个等式是他前一年发表的一个定理的应用，该定理可說是在历史上關於可求和发散级数的第一个定理。关于此求和法的详细内容请见下文；其中心思想是：1 − 2 + 3 − 4 + …是1 − 1 + 1 − 1 + …对1 − 1 + 1 − 1 + …的柯西乘积。

1 − 2 + 3 − 4 + … 以 1 − 1 + 1 − 1 + … 的双重柯西乘积表示

两个无穷级数的柯西乘积可被定義，即使在它们都发散的时候。例如，若Σa_n= Σb_n= Σ(−1)ⁿ，柯西乘积的项由有穷对角线求和的方式给出：

${\displaystyle {\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1)\end{array}}}$

积级数为：

${\displaystyle \sum _{n=0}^{\infty }(-1)^{n}(n+1)=1-2+3-4+\cdots }$

所以，如果有一种求和法可以保持两个级数的柯西乘积，並能得出${\displaystyle 1-1+1-1+\cdots ={\tfrac {1}{2}}}$的结果，那麼它也能够求出${\displaystyle 1-2+3-4+\cdots ={\tfrac {1}{4}}}$。由前一節的结果可知，当方法是线性、稳定并保持柯西乘积的时候，1 − 1 + 1 − 1 + …与1 − 2 + 3 − 4 + …的可求和之间是等价的。

切萨罗的定理是一个微妙的例子。级数1 − 1 + 1 − 1 + …在最弱的意义上是切萨罗可求和，称作(C, 1)-可求和，然而1 − 2 + 3 − 4 + …则需要切萨罗的定理的一个更强的形式^[5]，它是(C, 2)-可求和的。由于切萨罗的定理的所有形式均为线性且稳定的，所得的值正是此前计算所得的。

特殊方法

切萨罗与赫尔德

关于¹⁄₄的(H, 2)和的数据

若1 − 2 + 3 − 4 + …的(C, 1)切萨罗和存在，要找到其數值就需要计算该级数部分和的算术平均值。^[6] 部分和为：

1, −1, 2, −2, 3, −3, …,

这些部分和的算术平均值为：

1, 0,²⁄₃, 0,³⁄₅, 0,⁴⁄₇, ….

此平均值序列不收斂，因此1 − 2 + 3 − 4 + …不是切萨罗可求和。

切萨罗求和有两种有名的广义化：让这些在概念上更简单的是(H, n)法的序列，其中n为自然数。(H, 1)和为切萨罗求和，更高的方法则重复平均值的计算。在上文中，偶数項平均值趋近于¹⁄₂，奇数項平均值则全部等于0，所以平均值的平均值趋近于 0 与¹⁄₂的平均数，即¹⁄₄。^[7]因此，1 − 2 + 3 − 4 + …是(H, 2)-可求和，其值为¹⁄₄。

符号“H”代表奥图·赫尔德。1882年，他第一次证明了被现在数学家们所看作的在阿贝耳求和与(H, n)求和之间的关系；-1 + 2 − 3 + 4 − …是他給的第一个例子^[8]。¹⁄₄是1 − 2 + 3 − 4 + …的(H, 2)和这个事实也保证了它是阿贝耳和；这些都将在下文直接予以证明。

另外一个常用的切萨罗求和的广义化，是(C, n)法的序列。已经证明了(C, n)求和与(H, n)求和均能给出相同的结果，但是它们却有不同的历史背景。在1887年，切萨罗已经接近于陈述出(C, n)求和的定义了，但是他只给出了少量的例子。特别的，他在计算1 − 2 + 3 − 4 + …为¹⁄₄时所采用的方法可能是(C, n)的另一种描述，但是在当时并没有对其进行证明。他在1890年正式定义了(C, n)法，以陈述他的定理：一个(C, n)-可求和级数与一个(C, m)-可求和级数的柯西乘积是(C, m + n + 1)-可求和。^[9]

阿贝耳求和

1−2x+3x²+…的一些部分和（綠色、藍色和黑色曲線）；1/(1 + x)²（近中間的紫色曲線） ；以及在x趨近於1時的極限（以點標示）

在一份1749年的报告中，莱昂哈德·欧拉承认级数1 − 2 + 3 − 4 + …是发散的，但還是決定要对其求和：

……当說该级数1 − 2 + 3 − 4 + 5 − 6 …的和为¹⁄₄时，那肯定看起來是悖论。因為对该级数的100项相加，我们得到了-50，但是，101项的和却给出+51，这与¹⁄₄是截然不同的，而且这种差距还会随着项数增加而变得更大。不过我在前一段时间已经注意到了，有必要给“和”这个词赋予一个更加广泛的意义……。^[10]

欧拉曾几次提议将“和”这个词广义化。在1 − 2 + 3 − 4 + …的情况下，他的设想与现在所知的阿贝耳求和相似：

……毫无疑问，级数1 − 2 + 3 − 4 + 5 + …的和为¹⁄₄；由于它是由公式¹⁄_(1+1)²展开而成，而此公式的值明显为¹⁄₄。在考虑一般级数1 − 2x + 3x² − 4x³ + 5x⁴ − 6x⁵ + …后这个概念变得更明晰了。这个一般级数是由表达式¹⁄_(1+x)²展开而成，当我们让 x = 1 后，这个级数就确确实实地相等了。^[11]

至少在当绝对值 |x| < 1 时，有许多方式去验证欧拉的下列等式正确：

${\displaystyle 1-2x+3x^{2}-4x^{3}+\cdots ={\frac {1}{(1+x)^{2}}}}$

可以對右邊作泰勒展开，或使用正规的多项式长除。从左方开始，可采用上文的一般启发式，并尝试乘以两次(1+x)，或对几何级数1 − x + x² − …求平方。欧拉似乎也提出可以对后者级数的每项求導。^[12]

以现代的觀點看，级数 1 − 2x + 3x² − 4x³ + … 并没有定义一个在x = 1时的函数，因此不能简单地把值代入到其相應的表达式。不過由于此級數在|x| < 1時定义了一個函数，所以仍可取x趋近于1時的极限，而这就是阿贝耳和的定义：^[6]

${\displaystyle \lim _{x\rightarrow 1^{-}}\sum _{n=1}^{\infty }n(-x)^{n-1}=\lim _{x\rightarrow 1^{-}}{\frac {1}{(1+x)^{2}}}={\frac {1}{4}}}$

欧拉与波莱尔

¹⁄₂−¹⁄₄的欧拉求和

欧拉对该级数还使用了另外一种技巧：欧拉变换，这是他自己的发明。要计算欧拉变换，首先要有可形成交错级数的正项序列——在此情况下为1, 2, 3, 4, …。将此序列中的首项标示为 a₀。

下一步需要1, 2, 3, 4, …的前向差分序列；这恰好是1, 1, 1, 1, …。将该序列的首项标示为 Δa₀。欧拉变换也基于差分的差分，以及更高的迭代，但是在1, 1, 1, 1, …各項之間的前向差分均为0。1 − 2 + 3 − 4 + …的欧拉变换便可定义为：

${\displaystyle {\frac {1}{2}}a_{0}-{\frac {1}{4}}\Delta a_{0}+{\frac {1}{8}}\Delta ^{2}a_{0}-\cdots ={\frac {1}{2}}-{\frac {1}{4}}}$

用现代术语来说，1 − 2 + 3 − 4 + …是欧拉可求和且其值為¹⁄₄。

欧拉可求和也蘊涵了另一种可求和性。将1 − 2 + 3 − 4 + …表示为：

${\displaystyle \sum _{k=0}^{\infty }a_{k}=\sum _{k=0}^{\infty }(-1)^{k}(k+1)}$

就有了相关的处处收敛级数：

${\displaystyle a(x)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}(k+1)x^{k}}{k!}}=e^{-x}(1-x)}$

因此 1 − 2 + 3 − 4 + … 的波莱尔和为：^[13]

${\displaystyle \int _{0}^{\infty }e^{-x}a(x)\,dx=\int _{0}^{\infty }e^{-2x}(1-x)\,dx={\frac {1}{2}}-{\frac {1}{4}}}$

尺度分离

赛切夫与Woyczyński只通过两个物理原理便得出了1 − 2 + 3 − 4 + … =¹⁄₄，这两个原理分别是：无穷小松弛（infinitesimal relaxation）与尺度分离（separation of scales）。为求表達準确，这些原理促使了他們去定义一系列的“φ-求和法”，所有这些方法都可以将级数求和得¹⁄₄：

• 如果φ(x)是一个函数，其一、二阶导数在(0, ∞)上是连续且可积的，有φ(0) = 1 ，并且φ(x)与xφ(x)在+∞时的极限均为0，則：^[14]

${\displaystyle \lim _{\delta \downarrow 0}\sum _{m=0}^{\infty }(-1)^{m}(m+1)\varphi (\delta m)={\frac {1}{4}}}$

该结果推广了阿贝耳求和，当取φ(x) = exp(−x)时可得到先前的等式。此一般陈述可通过将关于m的级数中的项配对，并将表达式变换为黎曼积分的形式予以证明。在后一步中，对1 − 1 + 1 − 1 + …的相应证明（英语：Summation of Grandi's series#Separation of scales）运用了中值定理，但在这裡需要泰勒公式中更强的拉格朗日形式。

广义化

1755年的《Institutiones》上，欧拉对相似的级数求和

1 − 1 + 1 − 1 + …的三重柯西乘积为1 − 3 + 6 − 10 + …，为三角形数的交错级数；其阿贝耳与欧拉和为¹⁄₈。^[15]1 − 1 + 1 − 1 + …的四重柯西乘积为1 − 4 + 10 − 20 + …，为四面体数的交错级数，其阿贝耳和为¹⁄₁₆。

另一个1 − 2 + 3 − 4 + …在略微不同的方向的广义化是一般级数1 − 2ⁿ + 3ⁿ − 4ⁿ + …。对正整数n来说，此级数有下列的阿贝耳和：^[16]

${\displaystyle 1-2^{n}+3^{n}-\cdots ={\frac {2^{n+1}-1}{n+1}}B_{n+1}}$

其中B_n是伯努利数。对大於0的偶数n，则化約为：

${\displaystyle 1-2^{2k}+3^{2k}-\cdots =0}$

后一个和成为尼尔斯·亨利克·阿贝尔特别嘲笑的对象，在1826年時他說：

“发散级数纯粹是魔鬼的工作，胆敢去找到任何证明它们的行为都是羞耻的。如果用到它们，可以从中获得想要的东西；同时也是它们，制造了如此多的不愉快与如此多的悖论。试问能想到比下面内容更令人惊恐的东西吗：

0 = 1 − 2ⁿ + 3ⁿ − 4ⁿ + etc.

其中，n为正数。这是一个笑料，朋友。”^[17]

切萨罗的老师欧仁·查理·卡塔兰也轻视发散级数。在卡塔兰的影响下，切萨罗早期提出1 − 2ⁿ + 3ⁿ − 4ⁿ + …的“习用式”是“荒谬的等式”；而在1883年，切萨罗表明了当时的一个典型看法：這些公式是错的，不过在某些场合在形式上是有用的。最后，在他1890年的书《Sur la multiplication des séries》中，切萨罗從定義開始採用了一個現代的做法。^[18]

此级数在n为非整數值的情况亦有所研究；这产生了狄利克雷η函数。欧拉研究1 − 2 + 3 − 4 + …相关级数的部分动机是η函数的函数方程，这直接导向了黎曼ζ函数的函数方程。欧拉在正偶数（包括在巴塞尔问题中）时找到这些函数值的建树已让他闻名，他也试图找到正奇数（包括在阿培里常數中）时的值，但这个问题直到今天仍是難以解決的。η函数通过欧拉的方法解决会比較简单，因为它的狄利克雷级数是处处阿贝耳可求和；而ζ函数的狄利克雷级数則非常难以对发散的部分求和。^[19]例如，1 − 2 + 3 − 4 + …在η函数中的相似级数是非交错级数1 + 2 + 3 + 4 + …，该级数在现代物理学上有很深的应用，不过需要非常强的方法才能求和。

参见

• 伯努利数
• 黎曼ζ函数
• 泰勒级数
• 泛函方程

註釋

1. 「广义和」是指利用一些特殊的方式，計算发散级数的「和」，由於发散级数不會有一般定義下的和，因此稱為广义和。
2. 假定有這樣的極限值x，則總可能找到某個項，使得在其之後的所有項都在區間[x-1, x+1]之外，從而得出矛盾。

參考來源

1. Hardy p.8
2. Beals p.23
3. Hardy (p.6) 结合格兰迪级数1 − 1 + 1 − 1 + …的计算提出了此推导过程。
4. "One already writes(1 − 1 + 1 − 1 + …)² = 1 − 2 + 3 − 4 + …and asserts that both the sides are equal to${\displaystyle s={\begin{matrix}{\frac {1}{4}}\end{matrix}}}$.", Ferraro, p.130.
5. Hardy, p.3; Weidlich, pp.52–55.
6. B.A.卓里奇. 《数学分析》下册. 高等教育出版社. 2006: 346. ISBN 9787040202571.
7. Hardy, p.9. 要了解详细的计算过程，参看 Weidlich, pp.17–18.
8. Ferraro, p.118; Tucciarone, p.10. Ferraro批评了Tucciarone对赫尔德他自己对一般结论的看法的解释(p.7)，不过在赫尔德對-1 + 2 − 3 + 4 − …的处理方式上，两位作者的解释是相似的。
9. Ferraro, pp.123–128.
10. Euler et al, p.2. 虽然这篇文章写于1749年，但直到1768年才发表。
11. Euler et al, pp.3, 25.
12. 例如，Lavine (p.23)提倡多项式长除，但並没有真的列出計算步驟；Vretblad (p.231)计算了柯西乘积。欧拉的建议是含糊的；参看Euler et al, pp.3, 26。 约翰·贝兹甚至提出一种包括将点集与量子谐振子相乘的范畴理论法。Baez, John C. 欧拉对 1 + 2 + 3 + … = 1/12 的证明 (PDF) （页面存档备份，存于互联网档案馆）。 math.ucr.edu （2003年12月19日）。 2007年3月11日检索。
13. Weidlich p. 59
14. Saichev and Woyczyński, pp.260–264.
15. Kline, p.313.
16. Knopp, p.491; 在 Hardy, p.3. 中的这一点有误
17. Grattan-Guinness, p.80. 参看 Markushevich, p.48, 另一个法语转译版本；保留了原有的语调。
18. Ferraro, pp.120–128.
19. Euler et al, pp.20–25.

书目

• Beals, Richard. Analysis: an introduction. Cambridge UP. 2004. ISBN 0-521-60047-2.
• Davis, Harry F. Fourier Series and Orthogonal Functions. Dover. May 1989. ISBN 0-486-65973-9.
• Euler, Leonhard; Lucas Willis; and Thomas J Osler. Translation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series. The Euler Archive. 2006 [2007-03-22]. （原始内容存档于2012-07-10）. Originally published as Euler, Leonhard. Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques. Memoires de l'academie des sciences de Berlin. 1768, 17: 83–106.
• Ferraro, Giovanni. The First Modern Definition of the Sum of a Divergent Series: An Aspect of the Rise of 20th Century Mathematics. Archive for History of Exact Sciences. June 1999, 54 (2): 101–135. doi:10.1007/s004070050036.
• Grattan-Guinness, Ivor. The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press. 1970. ISBN 0-262-07034-0.
• Hardy, G.H. Divergent Series. Clarendon Press. 1949.
  LCCN 91-0 – 0
  .
• Kline, Morris. Euler and Infinite Series. Mathematics Magazine. November 1983, 56 (5): 307–314 [2007-04-20]. （原始内容存档于2019-08-21）.
• Lavine, Shaughan. Understanding the Infinite. Harvard UP. 1994. ISBN 0674920961.
• Markushevich, A.I. Series: fundamental concepts with historical exposition English translation of 3rd revised edition (1961) in Russian. Hindustan Pub. Corp. 1967.
  LCCN 68-0 – 0
  .
• Alexander I. Saichev, and Wojbor A. Woyczyński. Distributions in the physical and engineering sciences, Volume 1. Birkhaüser. 1996. ISBN 0-8176-3924-1.
• Tucciarone, John. The development of the theory of summable divergent series from 1880 to 1925. Archive for History of Exact Sciences. January 1973, 10 (1-2): 1–40. doi:10.1007/BF00343405.
• Vretblad, Anders. Fourier Analysis and Its Applications. Springer. 2003. ISBN 0387008365.
• Weidlich, John E. Summability methods for divergent series. Stanford M.S. theses. June 1950. OCLC 38624384.