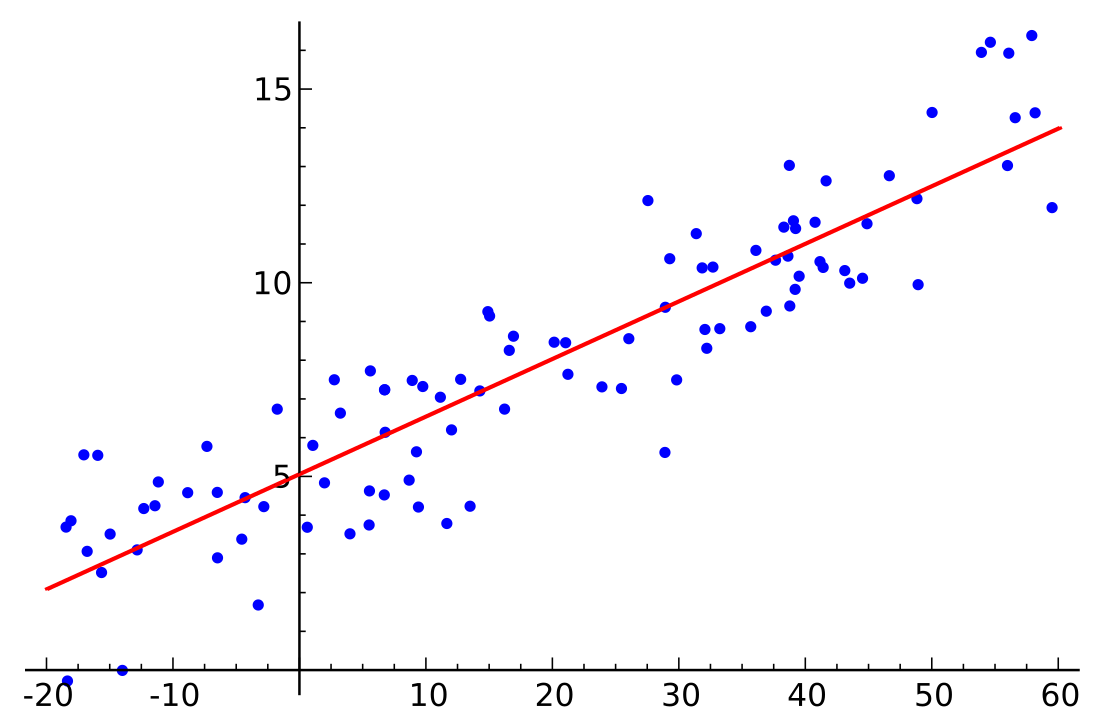
考虑一组 共
共 个数据点以及曲线(模型函数)
个数据点以及曲线(模型函数) 。该曲线同时取决于x与
。该曲线同时取决于x与 共n个参数(满足
共n个参数(满足 )。目标是找到在最小二乘意义上与数据点拟合最好的曲线所对应的参数
)。目标是找到在最小二乘意义上与数据点拟合最好的曲线所对应的参数 ,即最小化平方和
,即最小化平方和

其中残差ri的定义为

S取最小值时的梯度为零。由于模型包含n个参数,因此可得到n个梯度方程:

在非线性系统中,偏导数 同时是自变量x和参数
同时是自变量x和参数 的函数,因此这些梯度方程通常没有封闭解。因而必须为参数选择初始值用以迭代求解。迭代表达式为
的函数,因此这些梯度方程通常没有封闭解。因而必须为参数选择初始值用以迭代求解。迭代表达式为

其中,k是迭代次数, 则是偏移向量。每次迭代时,使用关于
则是偏移向量。每次迭代时,使用关于 的一阶泰勒级数展开以线性化模型:
的一阶泰勒级数展开以线性化模型:

雅可比矩阵J是常数、自变量与参数的函数,因此每次迭代时的J并不固定。对线性化模型而言,

残差的表达式则为


将上述表达式代入梯度方程,可以得到

以上方程可化简为n个联立的线性方程,称为正规方程(normal equations):

正规方程可用矩阵表示法写成

上述方程是使用高斯-牛顿算法求解非线性最小二乘问题的的基础。
需要注意的是雅可比矩阵定义中导数的符号约定。某些文献中的J可能与此处的定义相差一个负号。