来自维基百科，自由的百科全书
在幾何學中，五角六十面體是一種卡塔蘭立體[2]，為由60個不等邊五邊形組成的六十面體，並且是阿基米德立體扭棱十二面體的對偶多面體。[3][4]這種立體是一個等面圖形，也就是說它每個面都全等，但組成面不是正多邊形。五角六十面體有兩種不同的形式，它們互為鏡像（或“對映體”），是為手性鏡像，兩種手性鏡像的面、頂點、邊數皆相同，共有60個面、150個邊、92個頂點。五角六十面體是頂點數最多的卡塔蘭立體。在卡塔蘭立體和阿基米德立體中，五角六十面體的頂點數為第二多，僅次於具有120個頂點的大斜方截半二十面体。
五角六十面體是一個手性多面體[2]，也就是說，該多面體鏡射之後會跟原本的形狀不同，無法藉由旋轉半周再回到原本的形狀[5][6][7]。這兩種形式互為鏡像（或“對映體”），又稱為手性鏡像，且其面、頂點、邊數皆相同，共有60個面、150個邊、92個頂點[8][6][7]。在其92個頂點中，有80個頂點是三階頂點，即3個五邊形的公共頂點和12個頂點是五階頂點，即5個五邊形的公共頂點。[1]:97
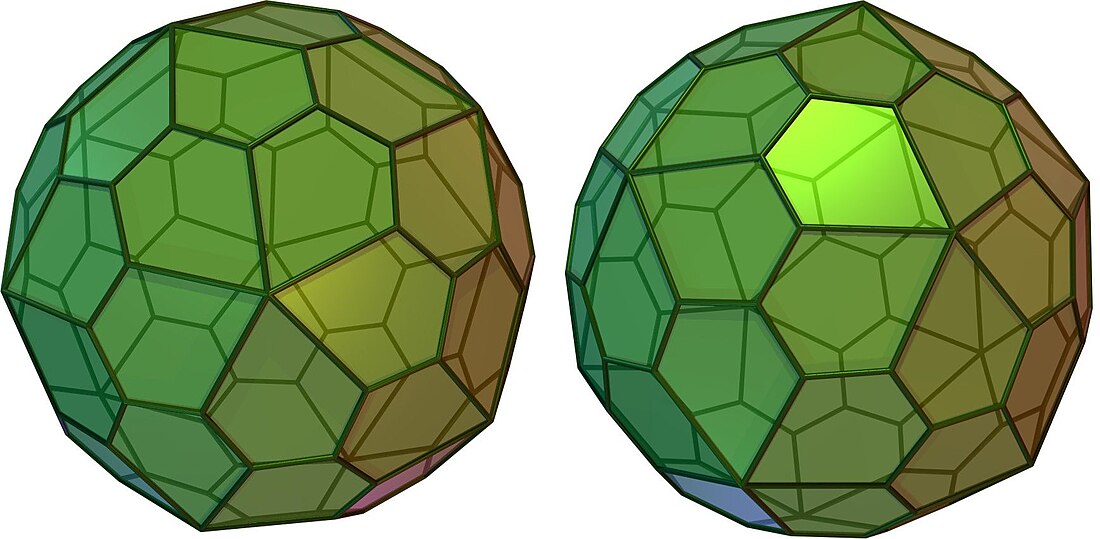
 五角六十面體的旋轉透視圖 |
 五角六十面體的另一個手性鏡像的旋轉透視圖 |
五角六十面體是扭棱十二面体的對偶多面體。事實上，五角六十面體可以不經由對偶變換而從扭棱十二面体構造。首先在扭棱十二面体的所有12個五邊形面上加入五角錐，再將扭棱十二面体的所有不與五邊形面相鄰的20個三角形面上加入三角錐，並調整加入之錐體的錐高，使加入的錐體之側面與其餘60個三角形面共面則形成五角六十面體，然而這種方式構造的五角六十面體會稍微有點形變。[9]
五角六十面體只有一種二面角，約為153.18度：[6][7]
五角六十面體60個全等的五邊形面組成，每個五邊形都具有3條短邊和2條長邊，若令為，則短邊與長邊的比為：[6][7]
其中為黃金比例。
若令為多項式的根，則長邊與短邊的比值為：
也就是說，若短邊為單位長，則長邊的長度約為1.74985單位長。
組成五角六十面體的五邊形有4個相等的鈍角和一個銳角（兩個長邊的夾角）。其中鈍角的角度為，約118度8分[1]:97，而反餘弦內的值是多項式的第一個實根[2]；銳角的角度為，約67度28分[1]:97，而反餘弦內的值是多項式的第4個根[2]。
扭棱十二面體的面心不能直接作為五角六十面體的頂點，因為4個三角形的面心位於同一個平面上，但五邊形的面心則否，它需要被徑向推出以使其與三角形中心共面。因此，五角六十面體的頂點並不都位於同一個球面上，因此根據定義，五角六十面體不是一個環帶多面體。
若其對偶多面體的邊長為單位長，則對應的五角六十面體八十個三階頂點所在的球面之半徑為：[6][7]
若要計算五角六十面體的體積和表面積，則需要將其中一個五邊形面的短邊表示為，並令常數為：[10]
則短邊長為的五角六十面體表面積（A）為：
體積（V）為：
使用以上這些數值，可以計算此形狀的球形度量值：
Seamless Wikipedia browsing. On steroids.
![{\displaystyle {\sqrt[{3}]{\tfrac {\varphi +{\sqrt {\varphi -{\tfrac {5}{27}}}}}{2}}}+{\sqrt[{3}]{\tfrac {\varphi -{\sqrt {\varphi -{\tfrac {5}{27}}}}}{2}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e4adb13b6f7a2a2daaf95dda9bf93df581d06487)
![{\displaystyle t={\frac {{\sqrt[{3}]{44+12\varphi (9+{\sqrt {81\varphi -15}})}}+{\sqrt[{3}]{44+12\varphi (9-{\sqrt {81\varphi -15}})}}-4}{12}}\approx 0.471\,575\,629\,622}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e12c93819b3df7ab0cb91ee980bdb2d27a34e53c)
