三次方程
未知项次数最高为3的整式方程 来自维基百科,自由的百科全书
三次方程是未知项總次数最高为3的整式方程,一元三次方程一般形式為
- ,
本條目只解釋一元三次方程,而且簡稱之為三次方程式。
历史
中國唐朝数学家王孝通在武德九年(626年)前后所著的《緝古算經》中建立了25个三次多项式方程和提出三次方程实根的数值解法。[1]
波斯数学家欧玛尔·海亚姆(1048年-1123年)通过用圆锥截面与圆相交的方法構建了三次方程的解法。他说明了怎样用这种几何方法利用三角法表得到数字式的答案。
中国南宋的数学家秦九韶在他1247年编写的《数书九章》一书中提出了高次方程的数值解法秦九韶算法,提出“商常为正,实常为负,从常为正,益常为负”的原则。
在十六世纪早期,意大利数学家费罗找到了能解一种三次方程的方法,也就是形如的方程。事实上,如果我们允许是複数,所有的三次方程都能变成这种形式,但在那个时候人们不知道複数。
尼科洛·塔爾塔利亞被認為是最早得出三次方程式一般解的人。1553年他在一場數學競賽中解出所有三次方程式的問題。隨後卡尔丹诺拜訪了塔爾塔利亞請教三次方程式解法並得到了啟發。卡尔丹诺注意到塔爾塔利亞的方法有时需要他给复数开平方。他甚至在《数学大典》裡包括了这些複數的计算,但他并不真正理解它。拉斐尔·邦贝利(Rafael Bombelli)详细地研究了这个问题,并因此被人们认为是複数的发现者。
判别式
当时,方程有一个实根和两个共轭複根;
当时,方程有三个实根:当
时,方程有一个三重实根;
当
时,方程的三个实根中有两个相等;
当时,方程有三个不等的实根。
三次方程解法
红色字体部分为判别式。
当时,方程有一个实根和两个共轭複根;
当时,方程有三个实根:
当时,方程有一个三重实根;
当时,方程的三个实根中有两个相等;
当时,方程有三个不等的实根。
,其中。
若令,则
令為域,可以進行開平方或立方運算。要解方程只需找到一個根,然後把方程除以,就得到一個二次方程,而我們已會解二次方程。
在一個代數封閉域,所有三次方程都有三個根。複數域就是這樣一個域,這是代數基本定理的結果。
解方程步驟:
- 把原來方程除以首項係數,得到:
- ,其中,,。
- 代換未知項,以消去二次項。當展開,會得到這項,正好抵消掉出現於的項。故得:
- ,其中和是域中的數字。
- ;。
- 設滿足,則為解
- 這個假設的hint如下:
- 記。前一方程化為。
- 展開:。
- 重組:。
- 分解:。
- 設和。我們有和因為。所以和是輔助方程的根,可代一般二次方程公式得解。
接下來,和是和的立方根,適合,,最後得出。
在域裡,若和是立方根,其它的立方根就是和,當然還有和,其中,是1的一个复数立方根。
因為乘積固定,所以可能的是,和。因此三次方程的其它根是和。
最先嘗試解的三次方程是實係數(而且是整數)。因為實數域並非代數封閉,方程的根的數目不一定是3個。所遺漏的根都在裡,就是的代數閉包。其中差異出現於和的計算中取平方根時。取立方根時則沒有類似問題。
可以證明實數根數目依賴於輔助方程的判別式,
- 若,方程有一个实根和两个共轭複根;
- 若,方程有三个实根:当时,方程有一个三重实根;当时,方程的三个实根中有两个相等;
- 若,方程有三个不等的实根:其中(注意,由於此公式應對於的形式,因此這裡的實際上是前段的,應用時務必注意取負號即)。
注意到实系数三次方程有一實根存在,這是因為非常數多項式在和的極限是無窮大,對奇次多項式這兩個極限異號,又因为多項式是連續函數,所以從介值定理可知它在某點的值為0。
解。
我們依照上述步驟進行:
- (全式除以)
- 設,代換:,再展開。
- ,,。設和。和是的根。
- 和,
- 和。
- ,
该方程的另外两个根:
- ,
- ,
这是一个历史上的例子,因为它是邦别利考虑的方程。
方程是。
从函数算出判别式的值,知道这方程有三实根,所以比上例更容易找到一个根。
前两步都不需要做,做第三步:,,。
- 和。
和是的根。这方程的判别式已算出是负数,所以只有实根。很吊诡地,这方法必须用到复数求出全是实数的根。这是发明复数的一个理由:复数是解方程必需工具,即使方程或许只有实根。
我们解出和。取复数立方根不同于实数,有两种方法:几何方法,用到辐角和模(把辐角除以3取模的立方根);代数方法,分开复数的实部和虚部: 现设。
- 等价于:
- (实部)
- (虚部)
- (模)
得到和,也就是,而是其共轭:。
归结得,可以立时验证出来。
其它根是和,其中。
当是负,和共轭,故此和也是(要适当选取立方根,记得);所以我们可确保是实数,还有和。
,其中系数皆为实数。
重根判别式:;
总判别式:。
。
让,得:
;
;
。
让,得:
;
。
让,得:
;
;
。
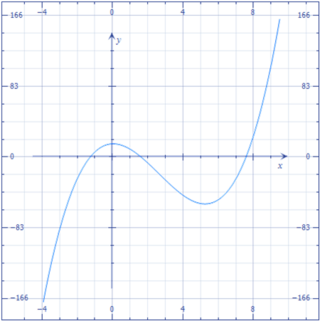
极值
设
将其微分,可得
- 有序列表项
设,可得。
由函数取极值的充分条件可知:
,是的极大值点;
,是的极小值点;
,是的拐点。
可知:
,的驻点为极大值点;
,的驻点为极小值点;
,的驻点为拐点。
參見
此章节尚無任何内容,需要扩充。 |
參考資料
外部链接
Wikiwand - on
Seamless Wikipedia browsing. On steroids.













![{\displaystyle x_{1}=-{\frac {b}{3a}}+{\sqrt[{3}]{{\frac {bc}{6a^{2}}}-{\frac {b^{3}}{27a^{3}}}-{\frac {d}{2a}}+{\sqrt {\color {red}\left({\frac {bc}{6a^{2}}}-{\frac {b^{3}}{27a^{3}}}-{\frac {d}{2a}}\right)^{2}+\left({\frac {c}{3a}}-{\frac {b^{2}}{9a^{2}}}\right)^{3}}}}}+{\sqrt[{3}]{{\frac {bc}{6a^{2}}}-{\frac {b^{3}}{27a^{3}}}-{\frac {d}{2a}}-{\sqrt {\left({\frac {bc}{6a^{2}}}-{\frac {b^{3}}{27a^{3}}}-{\frac {d}{2a}}\right)^{2}+\left({\frac {c}{3a}}-{\frac {b^{2}}{9a^{2}}}\right)^{3}}}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/46587b0851620fbebda9700bb088c1a03bb6788b)
![{\displaystyle x_{2}=-{\frac {b}{3a}}+{\frac {-1+{\sqrt {3}}\,{\rm {i}}}{2}}{\sqrt[{3}]{{\frac {bc}{6a^{2}}}-{\frac {b^{3}}{27a^{3}}}-{\frac {d}{2a}}+{\sqrt {\left({\frac {bc}{6a^{2}}}-{\frac {b^{3}}{27a^{3}}}-{\frac {d}{2a}}\right)^{2}+\left({\frac {c}{3a}}-{\frac {b^{2}}{9a^{2}}}\right)^{3}}}}}+{\frac {-1-{\sqrt {3}}\,{\rm {i}}}{2}}{\sqrt[{3}]{{\frac {bc}{6a^{2}}}-{\frac {b^{3}}{27a^{3}}}-{\frac {d}{2a}}-{\sqrt {\left({\frac {bc}{6a^{2}}}-{\frac {b^{3}}{27a^{3}}}-{\frac {d}{2a}}\right)^{2}+\left({\frac {c}{3a}}-{\frac {b^{2}}{9a^{2}}}\right)^{3}}}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9613fc132d7d8433ecc9fb0ea9f02107c76ce932)
![{\displaystyle x_{3}=-{\frac {b}{3a}}+{\frac {-1-{\sqrt {3}}\,{\rm {i}}}{2}}{\sqrt[{3}]{{\frac {bc}{6a^{2}}}-{\frac {b^{3}}{27a^{3}}}-{\frac {d}{2a}}+{\sqrt {\left({\frac {bc}{6a^{2}}}-{\frac {b^{3}}{27a^{3}}}-{\frac {d}{2a}}\right)^{2}+\left({\frac {c}{3a}}-{\frac {b^{2}}{9a^{2}}}\right)^{3}}}}}+{\frac {-1+{\sqrt {3}}\,{\rm {i}}}{2}}{\sqrt[{3}]{{\frac {bc}{6a^{2}}}-{\frac {b^{3}}{27a^{3}}}-{\frac {d}{2a}}-{\sqrt {\left({\frac {bc}{6a^{2}}}-{\frac {b^{3}}{27a^{3}}}-{\frac {d}{2a}}\right)^{2}+\left({\frac {c}{3a}}-{\frac {b^{2}}{9a^{2}}}\right)^{3}}}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5cb11b3a4399d17dcf4d7fb8961824c5c68ae9c7)

![{\displaystyle x=-{{b} \over {3a}}+{{{\sqrt[{3}]{2}}\left(b^{2}-3ac\right)} \over {3a\left({{-1+{\sqrt {3}}i} \over {2}}\right)^{k}}{\sqrt[{3}]{9abc-27a^{2}d-2b^{3}+{\sqrt {\left(9abc-27a^{2}d-2b^{3}\right)^{2}-4\left(b^{2}-3ac\right)^{3}}}}}}+{{\left({{-1+{\sqrt {3}}i} \over {2}}\right)^{k}}{\sqrt[{3}]{9abc-27a^{2}d-2b^{3}+{\sqrt {\left(9abc-27a^{2}d-2b^{3}\right)^{2}-4\left(b^{2}-3ac\right)^{3}}}}} \over {3{\sqrt[{3}]{2}}a}},k=0,1,2}](http://wikimedia.org/api/rest_v1/media/math/render/svg/90434371f77ff38cdd3892f9f9a111c90b4311e5)


![{\displaystyle x_{1}=-{\frac {b}{3a}}+2{\sqrt {-\beta }}\cos \left[{\frac {\arccos {\frac {\alpha }{(-\beta )^{\frac {3}{2}}}}}{3}}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2eff64fef380c6b55822a2d059f620320418d01d)
![{\displaystyle x_{2}=-{\frac {b}{3a}}+2{\sqrt {-\beta }}\cos \left[{\frac {\arccos {\frac {\alpha }{(-\beta )^{\frac {3}{2}}}}+2\pi }{3}}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5d8114ff094e6107e7d04f9033c6aaf245e223e6)
![{\displaystyle x_{3}=-{\frac {b}{3a}}+2{\sqrt {-\beta }}\cos \left[{\frac {\arccos {\frac {\alpha }{(-\beta )^{\frac {3}{2}}}}-2\pi }{3}}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7311682e035cebd9fb4d5c2ddf85b039b0b4fb23)













































































![{\displaystyle u={\sqrt[{3}]{\frac {-1-{\sqrt {5}}}{2}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/70eaa1e303a78012d9df600c1c08beb76493d46f)
![{\displaystyle v={\sqrt[{3}]{\frac {-1+{\sqrt {5}}}{2}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/fe45f167cf8e49f0aaddae06fb9fd909ab713a97)

![{\displaystyle ={\sqrt[{3}]{\frac {-1-{\sqrt {5}}}{2}}}+{\sqrt[{3}]{\frac {-1+{\sqrt {5}}}{2}}}-1\approx -1.3221853546}](http://wikimedia.org/api/rest_v1/media/math/render/svg/8b183fc86450a2b96880a21acb23c317fb9c0637)






























![{\displaystyle x_{1}={\frac {-b-\left({\sqrt[{3}]{y_{1}}}+{\sqrt[{3}]{y_{2}}}\right)}{3a}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/bc6d3541d2d3a5cacf10cf440484639df2fdbbf1)
![{\displaystyle x_{2}={\frac {-2b+\left({\sqrt[{3}]{y_{1}}}+{\sqrt[{3}]{y_{2}}}\right)+{\sqrt {3}}\left({\sqrt[{3}]{y_{1}}}-{\sqrt[{3}]{y_{2}}}\right){\rm {i}}}{6a}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2bfb02168a3d7421c640a871c2509d895b95c6f8)
![{\displaystyle x_{3}={\frac {-2b+\left({\sqrt[{3}]{y_{1}}}+{\sqrt[{3}]{y_{2}}}\right)-{\sqrt {3}}\left({\sqrt[{3}]{y_{1}}}-{\sqrt[{3}]{y_{2}}}\right){\rm {i}}}{6a}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b58850471736e2089de13440be01d1a259d72bc5)





















