Remove ads
混沌理論（粵拼：wan6 deon6 lei5 leon6；英文：chaos theory）係數學嘅一個子領域，研究「望落好似完全隨機同無法預測嘅系統」。精確啲講，套理論建基於蝴蝶效應－呢個諗頭講响非線性系統入面，就算初始狀態變咗少少，都可以引發好大影響，令個系統跟住落嚟嘅狀態完全唔同嗮[1][2]。
舉例說明，一座城市係個複雜嘅系統[3]：座城市由好多件部份組成，包括係市民、馬路等嘅基建以及建築物等好多樣嘢；想像喺市中心有位市民過馬路嗰陣唔小心（細微變化），有位司機為咗唔想撞到佢而撞咗埋第架車度，場交通意外搞到條馬路俾人封咗，於是多位市民返工返學有困難，咁啱得咁橋其中一位返唔到工嘅市民係某大企業嘅重要管理層，連帶搞到間企業當日嘅工作受阻，進而影響埋股市變化，引發經濟波動（系統跟住落嚟嘅狀態大變）。好似噉嘅連串變化就係「混沌」講緊嘅嘢－喺現實世界，好多時個系統嘅初始狀態係噉咦變咗啲，就會搞到個系統跟住出現意料之外嘅大變動[4]。
- 金融學：股市嘅上落受好多因素影響，例如利率以及供應同需求都會影響股價；家陣金融工作者想預測股市嘅變化，會唔會有可能利率升 0.1% 咁少，就搞到股市由正常狀態變成「引起恐慌性拋售，股價插水式下滑」呢？
- 醫學：人體嘅運作受好多因素影響，例如血入面各化學物質嘅濃度都可以影響人體能唔能夠正常運作；家陣醫護人員想喺病人身上用藥，會唔會隻藥嘅濃度升咗 0.1% 咁少，就搞到病人由「會好返」變成「會死」呢？
- 工程學：一部機械可以有極多件組成部份；想像家陣工程師想設計一部機械，會唔會部機嘅溫度或者壓力升咗 0.1% 咁少，就搞到部機由「正常噉行到落去」變成「會爆炸著火」呢？
... 呀噉。有好多唔同領域嘅工作者都有興趣研究混沌現象，除咗頭先提到嘅領域之外，氣候學[7]、生態學、各門嘅社會科學[8]以至電腦科學等嘅多個領域，都有工作者著手研究混沌。呢啲咁多唔同嘅研究就形成咗個跨學科嘅領域－混沌理論[5]。
Remove ads
混沌理論最基本嘅諗頭係所謂嘅蝴蝶效應（butterfly effect）：家吓將研究緊嘅現象想像成一個系統（尤其係複雜系統），當中「現象」可以係天氣、生態系統、人體、人腦、複雜嘅機械以至股市... 呀噉；一個系統梗會有某啲 input，而個系統跟住落嚟嘅狀態會取決於
- Input 同
- 系統打前嘅狀態；
事實表明，好多時 input 或者打前狀態變咗少少，跟住落嚟嘅變化就可以唔同嗮：
- 舉個具體例子，想像兩個經濟體（複雜系統）A 同 B，一開始嗰陣（）兩個經濟體狀態完全一樣咁滯，不過响一開始嗰時 A 嘅人口大過 B 少少，例如 A 人口係 100,002 而 B 人口係 100,000；直覺上會認為，A 同 B 跟住落嚟嘅變化會係一樣咁滯，但實際嘅研究發現並唔係噉－實證嘅研究表明，兩個經濟體有可能會隨時間變到完全唔一樣，例如 A 變成世界最大經濟體，同時 B 進入經濟衰退，最後 A 嘅 GDP 係 B 嘅 10 倍[9]。
- 噉嘅現象，喺經濟學以外嘅領域都可以觀察得到[10]，例如喺 1969 年，有科學家做過噉嘅研究－想像有隻蝴蝶喺度飛嚟飛去搵花蜜食；根據呢啲科學家計嘅數，隻蝴蝶拍翼會造成空氣嘅微細流動（細變化），而呢股微細變動有可能引起周圍嘅空氣出現一連串變化，最後喺地球另一邊引起龍捲風（意料之外嘅大變化）[11][12]。
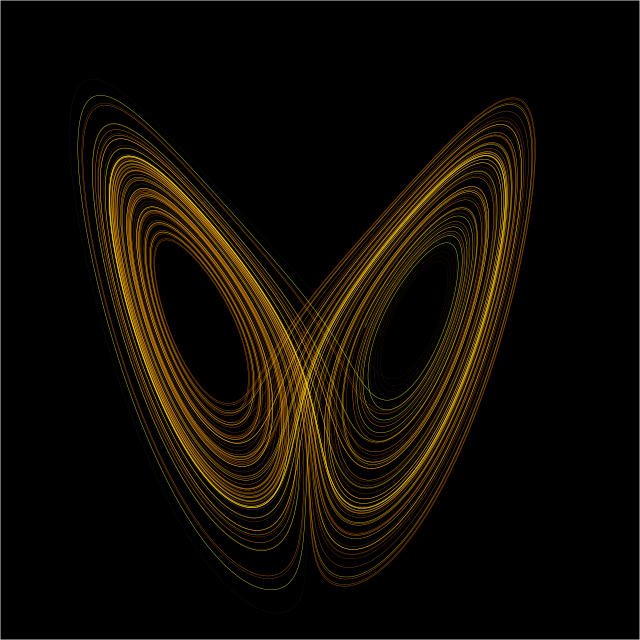
上述嘅現象仲可以用數學化嘅電腦模擬展示：附圖係混沌理論當中嘅洛倫茲系統（Lorenz system）嘅電腦模擬結果；成個系統有幾個變數同參數，包括 ，幅圖打戙嗰條軸做 ，打橫嗰條軸做時間，設 做「 嘅初始數值」，唔同色嘅線表示喺唔同 之下 隨時間變化嘅規律。由幅圖睇得出， 係噉咦變咗少少，就會令最後嘅 變化規律唔同嗮－嗰幾條唔同色嘅線大約去到 嗰陣分開。而且應用數學方面嘅研究仲發現，就算個系統完全冇任何隨機喺裏面（完全決定性），噉嘅現象依然有可能會發生[13]。
蝴蝶效應引起咗好多科研工作者嘅關注：科學嘅其中一個終極目的，就係想靠實證得到知識，用知識幫人類預測宇宙嘅各種現象，無論自然科學定社會科學都係噉；混沌嘅存在就正正係令到某啲現象難以預料，對人類預測現象嘅能力造成威脅。研究混沌嘅科學家會用數學化嘅方式思考混沌，並且嘗試將得出嘅數學模型應用落去現實嘅現象度，想從而加深人類對混沌現象嘅理解，解答「有冇方法可以預料混沌幾時會出現」等嘅問題[10]。
|
.jpg)
Remove ads
吸引子
内文：吸引子
複雜度
内文：複雜度
喺 19 世紀尾，法國數學家龐加萊（Henri Poincaré）等嘅研究者喺度諗太陽系啲天體嘅軌跡會點樣隨時間變化，佢哋用微分方程嚟做分析（用到隨時間嘅導數），發覺喺分析多過兩個天體嘅軌道嗰陣，啲現象經已複雜得滯，難以用公式描述，啲模型嘅可能結果由「啲天體冚唪唥都完美噉跟住現有嘅軌跡行」以至極端嘅「其中有粒行星俾重力掟出去太陽系外或者撞落太陽嗰度」都有；打後（用微分方程做）嘅研究又發現，有好多動態系統都有啲噉嘅情況－「只要啲初始條件嘅數值變咗少少，成個系統嘅狀態就會出現極端嘅變化」，而呢點就係混沌理論上所講嘅「混沌」。混沌嘅現象喺天氣、生態系統以至量子力學等多種現象嗰度都會見得到，係廿一世紀初數學界相當重視嘅一套理論[14]。
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
Remove ads