概率分佈一覽

以下係常用嘅概率分佈同相關概念一覽。

概率分佈（probability distribution）係指一個表明某個變數每個可能數值出現嘅機會率嘅函數，

${\displaystyle \Pr(X=x)=f(x)}$

當中 ${\displaystyle f}$ 就係個概率分佈；呢個函數可以畫做一個表，X 軸代表個目標變數嘅數值，Y 軸代表嗰個目標變數嘅每個數值出現嘅機率；是但搵個變數 ${\displaystyle X}$，${\displaystyle X}$ 喺總體當中有一個概率分佈，表示 ${\displaystyle X}$ 每個可能數值 ${\displaystyle x}$ 出現嘅機率，呢個分佈喺實際上係不可知嘅，研究者淨係有得攞樣本，量度樣本當中嘅概率分佈（喺個樣本入面，${\displaystyle X}$ 嘅每個可能數值出現嘅機率大約係幾多），靠噉嚟估計個總體嘅分佈^[1]。

喺廿一世紀統計學上，比較常用嘅概率分佈有以下呢啲：

離散概率分佈

内文：離散概率分佈

離散概率分佈（discrete probability distribution）：指所描述嘅變數 ${\displaystyle X}$ 嘅可能數值係離散嘅概率分佈^[2]。

• 概率質量函數（probability mass function，PMF）：描述一個離散概率分佈嘅函數；一個離散概率分佈嘅 PMF 會講明嗰個概率分佈嘅每一個離散可能數值出現嘅機會率^[2]：

  ${\displaystyle \sum p_{X}(x_{i})=1}$，啲可能性嘅機率冚唪唥加埋係 1；

  ${\displaystyle p(x_{i})>0}$，每個可能性嘅機率大過 0；

  ${\displaystyle p(x)=0{\text{ for all other x}}}$，啲可能性以外嘅數值出現嘅機會率係 0。

一個概率質量函數；${\displaystyle X}$ 嘅可能數值得三個（1、3 同 7），每個數值都掕住咗個「出現嘅機率」，而呢啲機率加埋係 1。

• 離散均勻分佈（discrete uniform distribution）：每個可能離散數值出現嘅機率都一樣，概率質量函數係^[2]：

  ${\displaystyle f(x)={\frac {1}{n}}}$，當中 ${\displaystyle n}$ 係 ${\displaystyle X}$ 有幾多個可能數值。

• 伯努利分佈（Bernoulli distribution）：描述嘅變數 ${\displaystyle k}$ 得兩個可能數值，數值係 1 嘅機會率係 ${\displaystyle p}$，數值係 0 嘅機會率係 ${\displaystyle q=(1-p)}$，概率質量函數 ${\displaystyle f(k;p)}$ 係^[3]：

  ${\displaystyle f(k;p)={\begin{cases}p&{\text{if }}k=1,\\q=1-p&{\text{if }}k=0.\end{cases}}}$

  • 廣義伯努利分佈（generalized Bernoulli distribution / multinoulli distribution）：描述嘅變數 ${\displaystyle k}$ 有 ${\displaystyle n}$ 個離散可能數值，概率質量函數係^[4]：

    ${\displaystyle f(i)={\begin{cases}p_{1}&{\text{if }}i=1,\\p_{2}&{\text{if }}i=2,\\p_{3}&{\text{if }}i=3,\\...\end{cases}}}$

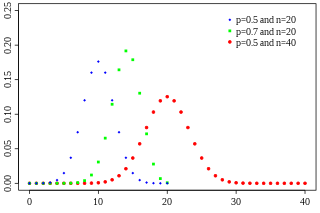
• 二項分佈（binomial distribution）：描述 ${\displaystyle n}$ 次結果二元嘅試驗；想像有個結果係二元－得兩個可能結果（1 同 0）－嘅試驗，例如掟銀仔，做 ${\displaystyle n}$ 咁多次，每次試驗嘅結果都有 ${\displaystyle p}$ 咁多機會率係 1， ${\displaystyle q=(1-p)}$ 咁多機會率係 0，而每次試驗嘅結果都係獨立嘅（一次試驗嘅結果唔受其他試驗嘅結果影響）。概率質量函數 ${\displaystyle f(k,n,p)}$，即係得出 ${\displaystyle k}$ 咁多個 1 嘅機會率係^[3]：

  ${\displaystyle f(k,n,p)=\Pr(k;n,p)=\Pr(X=k)={\binom {n}{k}}p^{k}(1-p)^{n-k}}$

  • 多項分佈（multinomial distribution）：係二項分佈嘅廣義化，描述嘅試驗有 ${\displaystyle k}$ 個可能結果，做 ${\displaystyle n}$ 咁多次（想像掟一粒 ${\displaystyle k}$ 面嘅骰仔掟 ${\displaystyle n}$ 咁多次）。概率質量函數係^[5]：

    ${\displaystyle f(k,n,p)={\frac {n!}{x_{1}!\cdots x_{k}!}}p_{1}^{x_{1}}\cdots p_{k}^{x_{k}}}$

一個二項分佈嘅概率質量函數圖；X 軸係 ${\displaystyle k}$。

• 幾何分佈（geometric distribution）：可以指兩個唔同嘅概率分佈，兩者都涉及一個結果二元嘅試驗^[6]：
  • 做咗個試驗 ${\displaystyle k}$ 次，終於得到 1 次陽性結果，而之前嗰啲試驗結果冚唪唥都係陰性：

    ${\displaystyle \Pr(X=k)=(1-p)^{k-1}p}$

    ${\displaystyle {\text{for }}k=1,2,3,...}$

  • ${\displaystyle k}$ 代表要做幾多次陰性試驗，先可以得到一次陽性結果：

    ${\displaystyle \Pr(Y=k)=(1-p)^{k}p}$

    ${\displaystyle {\text{for }}k=0,1,2,3,...}$

兩個幾何分佈嘅概率質量函數圖；X 軸係 ${\displaystyle k}$。

• 撥桑分佈（Poisson distribution）：模擬嘅事件有已知嘅平均發生率，而每件事件嘅發生彼此之間獨立，發生嘅次數設做 ${\displaystyle k}$，概率質量函數係^[7]：

  ${\displaystyle \!f(k;\lambda )=\Pr(X=k)={\frac {\lambda ^{k}e^{-\lambda }}{k!}}}$，當中 ${\displaystyle \lambda }$ 係預期會發生嘅次數（唔一定係整數）。

撥桑分佈嘅概率質量函數畫做圖嘅樣

連續概率分佈

内文：連續概率分佈

連續概率分佈（continuous probability distribution）：指所描述嘅變數 ${\displaystyle X}$ 嘅可能數值係連續嘅^[2]。

• 概率密度函數（probability density function，PDF）：描述一個連續概率分佈嘅函數；一個連續概率分佈嘅 PDF 會講明嗰個概率分佈嘅每一個可能數值出現嘅機會率大約係幾多^[2]，

  ${\displaystyle \Pr(X=x)=f(x)}$。

• 均勻分佈（continuous uniform distribution，簡稱 uniform distribution）：喺 ${\displaystyle a}$（最細可能數值）同 ${\displaystyle b}$（最大可能數值）之間嘅每個可能數值 ${\displaystyle x}$ 出現嘅機會率都一樣，概率密度函數係^[2]：

  ${\displaystyle {\begin{cases}{\frac {1}{b-a}}&{\text{for}}\ a\leq x\leq b,\\0&{\text{otherwise}}.\end{cases}}}$

• 常態分佈（normal distribution）：統計分析上最常用嘅概率分佈之一；喺常態分佈下，出現得最頻密嘅數值會係個平均數 ${\displaystyle \mu }$，而離平均數愈遠嘅數值就愈少會出現，畫做圖嘅話會出一條鐘形線（bell curve）；常見可以用常態分佈模擬嘅變數有人類嘅智商－多數人嘅智商數值都傾向於平均數，愈極端嘅數值愈少出現，即係話好少有智商極高或者極低嘅人。常態分佈個概率密度函數係（${\displaystyle \sigma }$ 係個分佈嘅標準差）^[1]：

  ${\displaystyle f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}}$

常態分佈畫做圖嘅樣；x 軸代表目標變數嘅數值，y 軸代表目標變數嘅每個數值出現嘅機會率 ${\displaystyle f(x)}$。

• 對數正態分佈（log-normal distribution）：指一個隨機變數嘅對數呈常態分佈；如果話 ${\displaystyle X}$ 呢個隨機變數呈對數正態分佈嘅話，噉 ${\displaystyle Y=\ln(X)}$ 呈常態分佈^[8]。

  ${\displaystyle \ln(X)\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$；當中 ${\displaystyle \mu }$ 係個常態分佈嘅平均值，而 ${\displaystyle \sigma }$ 係個常態分佈嘅標準差。

  其概率密度函數係：${\displaystyle f(x)={\frac {1}{x\sigma {\sqrt {2\pi }}}}\ \exp \left(-{\frac {\left(\ln x-\mu \right)^{2}}{2\sigma ^{2}}}\right)}$^[8]

• 柏里圖分佈（Pareto distribution）：常用嚟模擬人口隨時間增長嘅一個概率分佈^[9]，概率密度函數如下^[10]：

  ${\displaystyle f_{X}(x)={\begin{cases}{\frac {\alpha x_{\mathrm {m} }^{\alpha }}{x^{\alpha +1}}}&x\geq x_{\mathrm {m} },\\0&x<x_{\mathrm {m} }.\end{cases}}}$

  當中 ${\displaystyle x_{\mathrm {m} }}$ 係指 ${\displaystyle X}$ 嘅最細可能數值，而 ${\displaystyle \alpha }$ 係一個正嘅參數。

柏里圖分佈嘅 PDF 畫做圖嘅樣；當中 ${\displaystyle x_{\mathrm {m} }=1}$，而圖入面唔同嘅線代表唔同 ${\displaystyle \alpha }$ 數值下嘅 PDF。

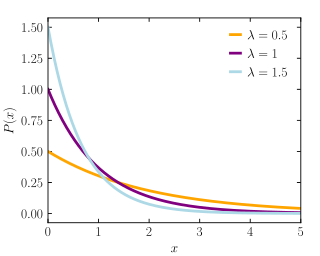
• 指數分佈（exponential distribution）：喺物理學上係常用嚟模擬一啲慢慢衰減嘅物理量嘅函數，例如係核衰變噉；喺統計學上，呢個函數可以用嚟模擬一啲機會率（${\displaystyle \Pr(X=x)}$）會隨住時間（${\displaystyle t}$）過去慢慢下降嘅事件，指數分佈嘅概率密度函數如下^[11]：

  ${\displaystyle f(x;\lambda )={\begin{cases}\lambda e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}}$

指數分佈嘅 PDF 畫做圖嘅樣；圖入面唔同嘅線代表唔同 ${\displaystyle \lambda }$ 數值下嘅 PDF。

分佈概念

• 頻率分佈（frequency distribution）：描述一個樣本入面每個可能數值出現咗幾多次嘅表^[12]。例：

身高間距	頻率	累計頻率
< 5.0 呎	25	25
5.0 - 5.5 呎	35	60
5.5 - 6.0 呎	20	80
6.0 - 6.5 呎	20	100

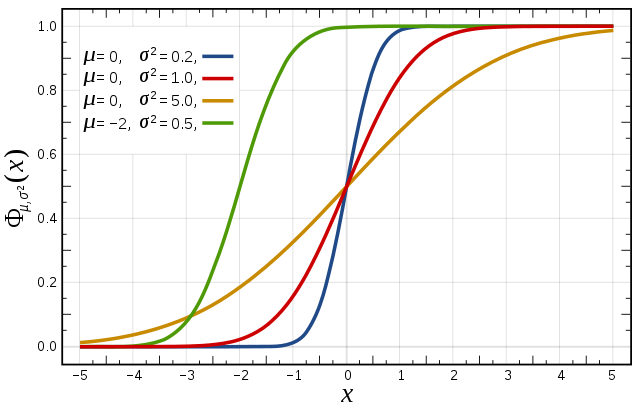
• 累計函數（cumulative distribution function）：描述一個概率分佈之下 ${\displaystyle X}$ 嘅累計值會點隨 ${\displaystyle x}$ 變化嘅函數 ${\displaystyle c(x)}$；${\displaystyle c(x_{0})}$ 表示「由個樣本嗰度隨機抽一個個體，個個體嘅 ${\displaystyle x}$（叫呢個值做 ${\displaystyle x_{d}}$）細過或者等如 ${\displaystyle x_{0}}$」嘅機會率，

  ${\displaystyle c(x_{0})=\Pr(x_{d}\leq x_{0})}$

  • 無論連續定離散嘅概率分佈都可以有相應嘅累計函數^[13]。

${\displaystyle \mu }$ 同 ${\displaystyle \sigma }$ 唔同嘅常態分佈嘅累計函數

• 對稱度（symmetry）：一個概率分佈可以有嘅一個屬性，攞個概率分佈當中嘅一個 ${\displaystyle x}$ 值，個分佈喺 ${\displaystyle x}$ 左邊嗰部份同個分佈喺 ${\displaystyle x}$ 右邊嗰部份形狀上愈相似，個概率分佈以 ${\displaystyle x}$ 為中心嘅對稱度就愈高；喺實際應用上，量度一個概率分佈嘅對稱度嗰陣會用嘅 ${\displaystyle x}$ 值通常會係個分佈嘅平均值^[14]。
  • 對稱概率分佈（symmetric probability distribution）：一個對稱概率分佈定義上係指符合下面呢條式嘅概率分佈，當中 ${\displaystyle x_{m}}$ 係個分佈上嘅一點^[14]：

    ${\displaystyle f(x_{m}-\delta )=f(x_{m}+\delta )}$ ${\displaystyle {\text{for}}}$ 所有實數 ${\displaystyle \delta }$

• 動差（moment）：泛指描述一個函數（例如概率分佈）嘅形狀嘅指標數值^[15]。
  • 偏度（skewness）：指個分佈有幾「歪埋一邊」；要評估一個分佈嘅偏度，一條可能嘅式如下：

    ${\displaystyle {\tilde {\mu }}_{3}=\operatorname {E} \left[\left({\frac {X_{i}-\mu }{\sigma }}\right)^{3}\right]}$；

    • 當中 ${\displaystyle X}$ 係第 ${\displaystyle i}$ 個個案嘅 ${\displaystyle x}$ 值，${\displaystyle \mu }$ 係個分佈嘅平均值，而 ${\displaystyle \sigma }$ 係個分佈嘅標準差；呢個數值愈大，表示個分佈偏度愈高^[16]。
  • 峰度（kurtosis）：指個分佈有幾「扁」；要評估一個分佈嘅偏度，一條可能嘅式如下：

    ${\displaystyle \operatorname {Kurt} [X]=\operatorname {E} \left[\left({\frac {X-\mu }{\sigma }}\right)^{4}\right]}$；

    • 當中 ${\displaystyle X}$ 係第 ${\displaystyle i}$ 個個案嘅 ${\displaystyle x}$ 值，${\displaystyle \mu }$ 係個分佈嘅平均值，而 ${\displaystyle \sigma }$ 係個分佈嘅標準差；呢個數值愈大，表示個分佈愈扁，（如果係常態分佈）比例上有愈多嘅個案處於極端值^[16]。

兩個有相當偏度嘅概率分佈

• 抽樣分佈（sampling distribution）：攞一個基於隨機抽樣嘅統計量，個統計量嘅概率分佈就係佢個抽樣分佈^[17]。
  • 標準誤差（standard error）：一個統計量嘅標準誤差係指佢抽樣分佈嘅標準差（SD）^[17]。
• 聯合概率分佈（joint probability distribution）：一個聯合概率分佈同時描述緊多過一個變數嘅分佈；一個兩變數聯合概率分佈會有打橫嘅 X 軸 Y 軸以及打戙嘅 Z 軸，總共三條軸，X 軸 Y 軸分別描述嗰兩個變數 ${\displaystyle X}$ 同 ${\displaystyle Y}$ 嘅數值，而 X 軸同 Y 軸成嘅平面當中每一點嘅高度（Z 值）反映咗「${\displaystyle X}$ 係呢個數值而且同時 ${\displaystyle Y}$ 係呢個數值」嘅機會率。當變數有多過兩個嗰陣同一道理^[18]。

一個兩變數聯合概率分佈

• 獨立同分佈（independent and identically distributed，iid）：係概率論同統計學上嘅一個概念；如果話一柞隨機性變數（或者事件）係「獨立同分佈」嘅話，意思係佢哋嘅概率分佈完全一樣（每次抽嗰陣個結果嘅概率分佈一樣），而且彼此之間獨立（抽一次嘅結果唔會受打前抽到嘅數值影響）^[19]。
• 中央極限定理（central limit theorem，CLT）：概率論同統計學上最重要嘅定理之一；根據 CLT，想像有個變數 ${\displaystyle x}$，只要三條條件成立：
  1. 個總體喺 ${\displaystyle x}$ 上嘅變異數係有限，
  2. 每次抽樣都係獨立同分佈（iid）嘅，
  3. 而且個樣本夠大，
  • 如果呢三條條件成立，噉無論個總體喺 ${\displaystyle x}$ 上嘅概率分佈係點嘅樣，而家做抽樣，個樣本喺 ${\displaystyle x}$ 上嘅平均值嘅分佈會接近一個常態分佈^[19]。

• 
  唔同 ${\displaystyle n}$ 同 ${\displaystyle p}$ ^{[註 1]}值嘅二項分佈出嘅樣本平均值嘅分佈；
  綠線：理論上嘅常態分佈（用嚟做對照）；
  紅線：嗰個 ${\displaystyle n}$ 同 ${\displaystyle p}$ 值組合出嘅樣本平均值分佈。

註釋

1. ${\displaystyle p}$ 係二項分佈當中有嘅一個參數。

睇埋

• 概率同統計學詞彙表