热门问题
时间线
聊天
视角
自由群
来自维基百科,自由的百科全书
Remove ads
在數學中,一個群 被稱作自由群,如果存在 的子集 使得 的任何元素都能唯一地表成由 中元素及其反元素組成之乘積(在此不論平庸的表法,例如 之類);此時也稱 為集合 上的自由群,其群結構決定於集合 ,記為 , 稱作一組基底。按照範疇論的觀點,自由群也可以抽象地理解為群範疇中的自由對象。

一個相關但略有不同的概念是自由阿貝爾群。
Remove ads
歷史
在1882年,Walther Dyck 在發表於 Mathematische Annalen 的論文 Gruppentheoretische Studien 中研究了自由群的概念,但未加以命名。「自由群」一詞由 Jakob Nielsen 於1924年引入。
例子
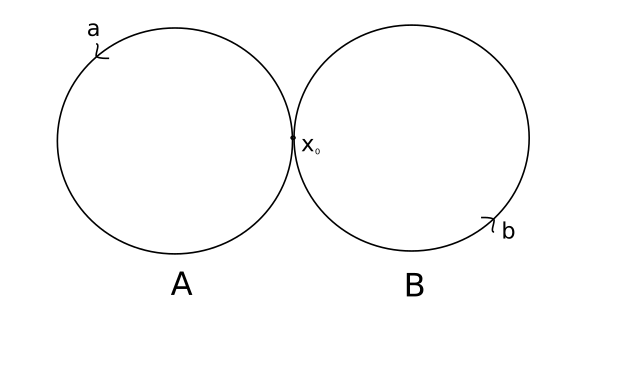
Remove ads
建構方式
今將構造集合 上之自由群 ,分解動作如下。
- 對任何 ,引入符號 ,稱作 的反元素。
- 考慮所有由符號 構成的有限字串。
- 如果一個字串能透過將 或 替換為空字串而變為另一個字串,則稱這兩個字串等價;此關係在所有上述字串構成的集合上生成一等價關係,其商集(等價類構成的集合)記作 。
- 我們可以藉著對字串長度作數學歸納法,證明此等價關係相容於字串的接合,即:。故字串接合在 導出二元運算,並滿足交換律。
- 取 及字串接合運算構成一個群,字串 之逆為 。此即所求。
若 為空集,則 為平凡群。
Remove ads
泛性質
上述構造 帶有一個自然的集合映射 。這對資料 滿足以下泛性質:
- 若 為群, 為集合間的映射,則存在唯一的群同態 使得 。
事實上我們僅須,也必須設 ;前述構造確保此式給出一個明確定義的群同態。
任兩個滿足上述泛性質的資料 、 至多差一個同構,因而刻劃了自由群的群論性質。這種泛性質是泛代數中考慮的自由對象的特例,用範疇論的語言來說,函子 是遺忘函子的左伴隨函子。
Remove ads
性質與定理
- 任何群 皆可表為某個自由群的同態像;在上述泛性質中取 為 的一組生成集,ψ 為包含映射即可。此時 的核 稱作關係, 稱作 的一個展示;若 有限,則稱之為有限展示。一個群可以有多種展示,而且不存在判斷兩個展示給出的群是否同構的演算法。
- 如果 有超過一個元素,則 非交換;事實上 的中心只有單位元素。
- 任兩個自由群 同構的充要條件是 基數相同,此基數稱作自由群的階。
以下是一些相關定理:
- Jakob Nielsen 與 Otto Schreirer 的定理:自由群的子群也是自由群。若 為 階,,則 為 階(在此設 有限)。
- 設 為超過一階的自由群;則對任意可數基數 , 中都存在 階的自由子群。
自由群雖然看似是離散的對象,卻可藉微分幾何或拓撲學工具研究,上述 Nielsen-Schreirer 定理就是一例(可運用同倫上纖維的構造證明);這套技術屬於幾何群論的一支。
Remove ads
自由阿貝爾群
將上述泛性質中的「群」替換成「阿貝爾群」,遂得到自由阿貝爾群的泛性質。集合 上的自由阿貝爾群可視為自由 -模來構造,或取作 的「交換化」: (換言之,在考慮字串時不計符號順序)。
Remove ads
塔斯基的問題
塔斯基在1945年左右提出下述問題:
目前已有兩個團隊獨立給出肯定的答案,但雙方的證明都尚未被認可。請參見網址 [1] 的「O8」。
文獻
- Kharlampovich, Olga; Myasnikov, Alexei, Elementary theory of free non-abelian groups, J. Algebra, 2006, 302 (2): 451–552, doi:10.1016/j.jalgebra.2006.03.033, 數學評論2293770
- W. Magnus, A. Karrass and D. Solitar, "Combinatorial Group Theory", Dover (1976).
- Sela, Z., Diophantine geometry over groups. VI. The elementary theory of a free group., Geom. Funct. Anal. 16, 2006, (3): 707–730, 數學評論2238945
- J.-P. Serre, Trees, Springer (2003) (English translation of "arbres, amalgames, SL2", 3rd edition, astérisque 46 (1983))
Remove ads
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads






































![{\displaystyle F(S)/[F(S),F(S)]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/436c79080d04b0cb47c3a2f08f0b8163be559852)