正切

正切（Tangent，${\displaystyle \tan }$，東歐國家將其寫作tg）是三角函數的一種。它的值域是整個實數集，定義域落在${\displaystyle \left\{x|x\neq k\pi +{\tfrac {\pi }{2}},k\in \mathbb {Z} \right\}}$（${\displaystyle \left\{x\in \mathbb {R} |x\neq 180^{\circ }k+90^{\circ },\,k\in \mathbb {Z} \right\}}$）。它是周期函數，其最小正周期為${\displaystyle \pi }$（180°）。正切函數是奇函數。

正切
性質
奇偶性	奇
定義域	${\displaystyle \left\{x\in \mathbb {R} |x\neq k\pi +{\tfrac {\pi }{2}},\,k\in \mathbb {Z} \right\}}$ ${\displaystyle \left\{x\in \mathbb {R} |x\neq 180^{\circ }k+90^{\circ },\,k\in \mathbb {Z} \right\}}$
到達域	(-∞,∞)
周期	${\displaystyle \pi }$ （180°）
特定值
當x=0	0
當x=+∞	N/A
當x=-∞	N/A
最大值	∞
最小值	-∞
其他性質
漸近線	${\displaystyle x=\left(2k+1\right){\tfrac {\pi }{2}}}$ （x=180°k+90°）
根	${\displaystyle k\pi }$ （180°k）
不動點	當x軸為弧度時： 0 ±4.4934094579091... （±257.453397562356...°） ±7.7252518369378... （±442.6243259322...°） ±10.9041216594289... （±624.7601503824636...°） ... 當x軸為角度時： 0 ±89.35883916555255...° ±269.78762733604602...° ±449.8726402096397...° ...
k是一個整數。

符號說明

正切的符號為${\displaystyle \tan }$，源於英文tangent。該符號最早由數學家湯瑪斯·芬克（英語：Thomas Fincke）（Thomas Fincke）所採用。

定義

直角三角形中

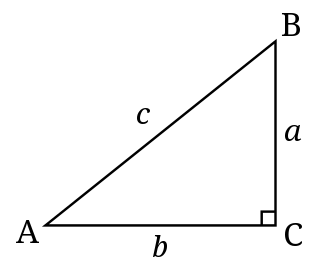直角三角形，∠C為直角，∠A 的角度為 ${\displaystyle \theta }$， 對於 ∠A 而言，a為對邊、b為鄰邊、c為斜邊

在直角三角形中，一個銳角的正切定義為它的對邊與鄰邊的比值，也就是：

${\displaystyle \tan \theta ={\frac {\text{a}}{\text{b}}}={\frac {\sin \theta }{\cos \theta }}\,\!}$

可以發現其定義和餘切函數互為倒數。

直角坐標系中

設${\displaystyle \alpha }$是平面直角坐標系xOy中的一個象限角，${\displaystyle P\left({x,y}\right)}$是角的終邊上一點，${\displaystyle r={\sqrt {x^{2}+y^{2}}}>0}$是P到原點O的距離，則α的正切定義為：

${\displaystyle \tan \alpha ={\frac {y}{x}}}$

單位圓定義

單位圓

圖像中給出了用弧度度量的某個公共角。逆時針方向的度量是正角而順時針的度量是負角。設一個過原點的線，同x軸正半部分得到一個角θ，並與單位圓相交，並令這個交點為y。另原點為O。做一直線，y點，垂直於${\displaystyle {\overline {Oy}}}$，並與單位圓相切，令直線與x軸的交點，則此點與y點之距離為正切比值。

單位圓上的正切

單位圓可以被認為是通過改變鄰邊和對邊的長度並保持斜邊等於1查看無限數目的三角形的一種方式。

對於大於${\displaystyle 2\pi }$（360°）或小於${\displaystyle -2\pi }$（-360°）的角度，簡單的繼續繞單位圓旋轉。在這種方式下，有些三角函數變成了周期為${\displaystyle 2\pi }$（360°）的周期函數；但由於正切是切線，再繞單位圓旋轉時，會出現周期是${\displaystyle \pi }$（180°），所以正切是周期為π（180°）的周期函數：

${\displaystyle \tan \theta =\tan \left(\theta +\pi k\right)=\tan \left(\theta +180^{\circ }k\right)}$

對於任何角度${\displaystyle \theta }$和任何整數${\displaystyle k}$。

級數定義

正切函數也可以使用泰勒展開式定義

${\displaystyle \tan x=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+{\frac {17x^{7}}{315}}+{\frac {62x^{9}}{2835}}+...=\sum _{n=1}^{\infty }{\frac {B_{2n}4^{n}(4^{n}-1)}{(2n)!}}x^{2n-1}}$

其中${\displaystyle B_{2n}}$為伯努利數。

另外，我們也有

${\displaystyle \tan x=8x\sum _{k=1}^{\infty }{\frac {1}{(1-2k)^{2}\pi ^{2}-4x^{2}}}.}$

微分方程定義

${\displaystyle \tan }$的微分是${\displaystyle \sec }$的平方

${\displaystyle {\frac {d}{dx}}\tan x\ =\sec ^{2}x}$

另外

${\displaystyle \int \tan x\,dx=-\ln(\cos x)}$

所以可以用

${\displaystyle \tan x=(-\ln(\cos x))'\,}$來定義。

指數定義

${\displaystyle \tan \theta ={\frac {e^{{\mathrm {i} }\theta }-e^{-{\mathrm {i} }\theta }}{{\mathrm {i} }(e^{{\mathrm {i} }\theta }+e^{-{\mathrm {i} }\theta })}}\,}$

恆等式

用其它三角函數來表示正切

函數	sin	cos	tan	cot	sec	csc
${\displaystyle \tan \theta }$	${\displaystyle {\frac {\sin \theta }{\sqrt {1-\sin ^{2}\theta }}}}$	${\displaystyle {\frac {\sqrt {1-\cos ^{2}\theta }}{\cos \theta }}}$	${\displaystyle \tan \theta \ }$	${\displaystyle {\frac {1}{\cot \theta }}}$	${\displaystyle {\sqrt {\sec ^{2}\theta -1}}}$	${\displaystyle {\frac {1}{\sqrt {\csc ^{2}\theta -1}}}}$

角的和差

${\displaystyle \tan(\theta \pm \psi )={\frac {\tan \theta \pm \tan \psi }{1\mp \tan \theta \tan \psi }}}$

正切的有限多項和

設${\displaystyle x_{i}=\tan(\theta _{i})}$，對於${\displaystyle i=1,\ldots ,n}$。設${\displaystyle e_{k}}$是變量${\displaystyle x_{i}}$，${\displaystyle i=1,\ldots ,n}$，${\displaystyle k=0,\ldots ,n}$的${\displaystyle k}$次基本對稱多項式。則

${\displaystyle \tan(\theta _{1}+\cdots +\theta _{n})={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-e_{2}+e_{4}-\cdots }},}$

項的數目依賴於${\displaystyle n}$。例如，

${\displaystyle {\begin{aligned}\tan(\theta _{1}+\theta _{2}+\theta _{3})&{}={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_{3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3})}},\\\\\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&{}={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\\\&{}={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4}+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}},\end{aligned}}}$

並以此類推。一般情況可通過數學歸納法證明。

半角公式

${\displaystyle {\begin{aligned}\tan {\frac {\theta }{2}}&=\csc \theta -\cot \theta \\&=\pm \,{\sqrt {1-\cos \theta \over 1+\cos \theta }}\\&={\frac {\sin \theta }{1+\cos \theta }}\\&={\frac {1-\cos \theta }{\sin \theta }}\\&={\frac {\cos \theta +\sin \theta -1}{\cos \theta -\sin \theta +1}}\end{aligned}}}$

二倍角

${\displaystyle {\begin{aligned}\tan 2\theta &={\frac {2\tan \theta }{1-\tan ^{2}\theta }}\\&={\frac {1}{1-\tan \theta }}-{\frac {1}{1+\tan \theta }}\\\end{aligned}}}$

三倍角

${\displaystyle \tan 3\theta ={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}}$

正切定理

主條目：正切定理

一個三角形。它的三個內角及其對邊。

在平面三角形中，正切定理說明任意兩條邊的和除以第一條邊減第二條邊的差所得的商等於這兩條邊的對角的和的一半的正切除以第一條邊對角減第二條邊對角的差的一半的正切所得的商。即：

${\displaystyle {\frac {a-b}{a+b}}={\frac {\mathrm {tan} \,{\frac {\alpha -\beta }{2}}}{\mathrm {tan} \,{\frac {\alpha +\beta }{2}}}}}$

${\displaystyle {\frac {b-c}{b+c}}={\frac {\mathrm {tan} \,{\frac {\beta -\gamma }{2}}}{\mathrm {tan} \,{\frac {\beta +\gamma }{2}}}}}$

${\displaystyle {\frac {c-a}{c+a}}={\frac {\mathrm {tan} \,{\frac {\gamma -\alpha }{2}}}{\mathrm {tan} \,{\frac {\gamma +\alpha }{2}}}}}$

用途

物理學

當一物體在斜面上剛開始滑動時，其靜摩擦係數為斜面傾角的正切值。

參見

• 正弦
• 餘弦
• 餘切
• 餘割
• 正割
• 三角學
• 三角函數