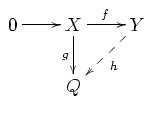內射模
数学术语 来自维基百科,自由的百科全书
內射模(英語:injective module),在模論中,是具有與有理數 (視為 -模)相似性質的模。內射模是投射模的對偶概念,由Reinhold Baer於1940年引進。
定義
一個環 上的左模 若滿足以下等價條件,則稱之為內射模:
- 若 是另一個左 -模 的子模,則存在另一個子模 使得 。
- 若 是左 -模的單射, 為同態,則存在同態 使得 。圖示如下:
右模的定義類此。抽象地說,內射模乃是模範疇中的內射對象。
例子
- 零模是內射模的平凡例子。
- 設 為域,則任何 -模(即 -向量空間)都是內射模,此點可由基的性質證明。
- 設 為緊群(例如有限群), 為特徵為零的域。根據緊群的表示理論,可知任何表示的子表示都是其直和項;若翻譯為模的語言,即是:群代數 上的所有模都是內射模。
- 設 為域 上含單位元的有限維結合代數。則逆變函子 給出有限生成左 -模與有限生成右 -模的對偶性。因此,有限生成的左 -模在同構的意義下皆可寫作 ,其中 是某個有限生成的投射右 -模。
- 在一般的環上也存在充足的(在內射分解的意義下)投射模,以下將述及相關理論。初步的例子包括: 對加法形成內射 -模。群 ()是內射 -模,而非內射 -模。
- 若一個環作為它自身的左模是內射的,就稱為一個左自內射環(英語:left self-injective ring)。右自內射環可對稱的定義。半單環,整數的剩餘類環是自內射環。一個左自內射環不一定是右自內射的。
性質
內射模的直積(包括無窮直積)仍是內射模,內射模的有限直和仍為內射模。一般而言,內射模的子模、商模或無窮直和並不一定是內射模。
Baer 在其論文中證明了一個有用的結果,通常稱作 Baer 判準:一個左 -模 是內射模若且唯若定義在任一理想 上的態射 都能延拓到整個 上。
利用此判準,可證明主理想域 上的模 是內射模若且唯若 可除,即:對任何 ,存在 使得 ,由此可證 是內射 -模,向量空間都是內射模。
最重要的內射模當屬 :它是 -模範疇中的內射上生成元,換言之,這是內射模,而且任何 -模皆可嵌入某個 中,其中 是夠大的基數。由此可知任何 -模皆可嵌入某個內射 -模。此性質對任意環 上的左模都成立,要點在於利用 的特性構造左 -模範疇中的內射上生成元。
我們也可以定義模的內射包(基本上是包含一個模的最小內射模)。任意模 都有內射分解,這是形式如下的正合序列:
其中每個 都是內射的。內射分解可以用以定義模的內射維度(基本上是內射分解的最短長度,可能是無限的)及導函子。
不可分解內射模的自同態環是局部環。
文獻
- F.W. Anderson and K.R. Fuller: Rings and Categories of Modules, Graduate Texts in Mathematics, Vol. 13, 2nd Ed., Springer-Verlag, New York, 1992.
參見
Wikiwand - on
Seamless Wikipedia browsing. On steroids.