维纳过程

数学中，维纳过程（英语：Wiener process）是一种连续时间随机过程，得名于诺伯特·维纳。由于与物理学中的布朗运动有密切关系，也常被称为“布朗运动过程”或简称为布朗运动。维纳过程是莱维过程（指左极限右连续的平稳独立增量随机过程）中最有名的一类，在纯数学、应用数学、经济学与物理学中都有重要应用。

一维的维纳过程的一个路径

三维的维纳过程的一个路径

维纳过程的地位在纯数学中与在应用数学中同等重要。在纯数学中，维纳过程导致了对连续鞅理论的研究，是刻画一系列重要的复杂过程的基本工具。它在随机分析、扩散过程和位势论领域的研究中是不可或缺的。在应用数学中，维纳过程可以描述高斯白噪声的积分形式。在电子工程中，维纳过程是建立噪音的数学模型的重要部分。控制论中，维纳过程可以用来表示不可知因素。

维纳过程和物理学中的布朗运动有密切关系。布朗运动是指悬浮在液体中的花粉微小颗粒所进行的无休止随机运动。维纳运动也可以描述由福克-普朗克方程和郎之万方程确定的其他随机运动。维纳过程构成了量子力学的严谨路径积分表述的基础（根据费曼-卡茨公式，薛定谔方程的解可以用维纳过程表示）。金融数学中，维纳过程可以用于描述期权定价模型如布莱克-斯科尔斯模型。

刻画维纳过程

一个维纳过程（也称为标准布朗运动）${\displaystyle W_{t}}$可以用三个性质刻画^[1]:§7.1

1. ${\displaystyle W_{0}=0}$
2. 映射${\displaystyle t\mapsto W_{t}}$在正实数轴上几乎处处连续
3. ${\displaystyle W_{t}}$是独立增量函数，并且对所有${\displaystyle 0\leqslant s<t}$，${\displaystyle W_{t}-W_{s}\,\,\sim {\mathcal {N}}(0,t-s)}$

第三条中，${\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}$表示期望为${\displaystyle \mu }$，方差为${\displaystyle \sigma ^{2}}$的正态分布随机变量。独立增量函数的定义是，如果随机抽取两段不重叠的时间段 ${\displaystyle 0\leqslant s_{1}<t_{1}\leqslant s_{2}<t_{2}}$，${\displaystyle W_{t_{1}}-W_{s_{1}}}$和${\displaystyle W_{t_{2}}-W_{s_{2}}}$是互相独立的随机变量，并且对更多的不重叠时间段的情况也是如此

另一个等价的刻画方式是以法国数学家保罗·利维命名的“利维刻画”：维纳过程是几乎处处路径连续的零期望连续鞅，并且满足二次变差：${\displaystyle \langle W,W\rangle _{t}}$，也就是说${\displaystyle W_{t}^{2}-t}$仍然是连续鞅。

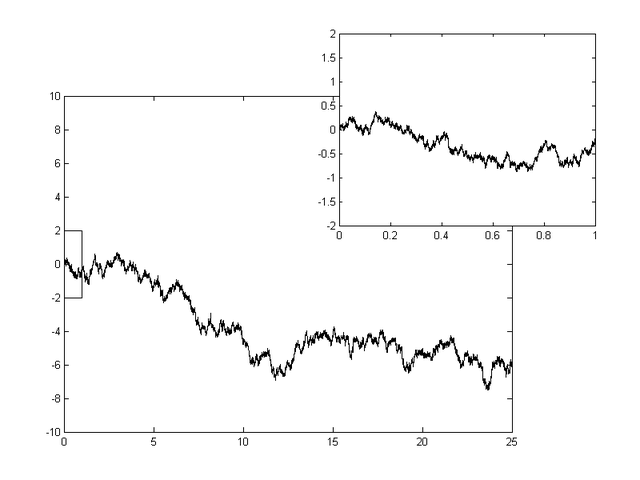
1923年，维纳首次证明维纳过程存在^[2]:9。维纳过程可以用随机漫步或任意拥有平稳独立增量的离散随机过程的尺度极限来构造。这个构造方法基于Donsker定理。与随机漫步一样，一维和二维的维纳过程是常返的，也就是说几乎一定会回到起始的原点，或者说几乎一定会无限次跌入原点附近的任意邻域。当维度高于或等于三维时，维纳过程不再是常返的。与随机漫步不同的是，维纳过程拥有尺度不变性。如果${\displaystyle W_{t}}$是一个随机过程，那么对所有的正实数${\displaystyle \alpha }$，

${\displaystyle {\frac {1}{\alpha }}W_{\alpha ^{2}t}\,}$

也是一个维纳过程^[2]:12。

维纳测度是满足 ${\displaystyle g(0)=0}$ 的连续函数空间上的概率分布^{[需要解释]}。关于维纳测度的积分称为 维纳积分.

一维维纳过程的性质

基本性质

对任意的正实数${\displaystyle t}$，一维维纳过程在${\displaystyle t}$时刻是一个随机变量，它的概率密度函数是：${\displaystyle f_{W_{t}}(x)={\frac {1}{\sqrt {2\pi t}}}e^{-x^{2}/{2t}}.}$

这是因为按照维纳过程的定义，当${\displaystyle s=0}$时，可以推出${\displaystyle W_{t}}$的分布：

${\displaystyle W_{t}=W_{t}-W_{0}\sim {\mathcal {N}}(0,t).}$

它的数学期望是零：${\displaystyle \mathbb {E} (W_{t})=0.}$ 它的方差是${\displaystyle t}$：${\displaystyle \operatorname {Var} (W_{t})=\mathbb {E} (W_{t}^{2})-\mathbb {E} ^{2}(W_{t})=\mathbb {E} (W_{t}^{2})-0=\mathbb {E} (W_{t}^{2})=t.}$

在维纳过程的独立增量定义中，令${\displaystyle t_{2}=t}$，${\displaystyle s_{2}=t_{1}=s<t}$，${\displaystyle s_{1}=0}$，那么${\displaystyle W_{s}=W_{t_{1}}-W_{s_{1}}\sim {\mathcal {N}}(0,s)}$和${\displaystyle W_{t}-W_{s}=W_{t_{2}}-W_{s_{2}}\sim {\mathcal {N}}(0,t-s)}$是相互独立的随机变量，并且

${\displaystyle \operatorname {cov} (W_{s},W_{t})=\mathbb {E} \left[(W_{s}-\mathbb {E} (W_{s}))\cdot (W_{t}-\mathbb {E} (W_{t}))\right]=\mathbb {E} (W_{s}\cdot W_{t})=\mathbb {E} [W_{s}\left(W_{t}-W_{s}\right)]+\mathbb {E} (W_{s}^{2})=\mathbb {E} (W_{s})\mathbb {E} \left(W_{t}-W_{s}\right)+s=s\ \ .}$

所以两个不同时刻${\displaystyle 0\leqslant s,t}$，${\displaystyle W_{t}}$与${\displaystyle W_{s}}$的协方差和相关系数是：

${\displaystyle \operatorname {cov} (W_{s},W_{t})=\min(s,t)\,,\qquad \quad \operatorname {corr} (W_{s},W_{t})={\mathrm {cov} (W_{s},W_{t}) \over \sigma _{W_{s}}\sigma _{W_{t}}}={\frac {\min(s,t)}{\sqrt {st}}}={\sqrt {\frac {\min(s,t)}{\max(s,t)}}}\,.}$

即时最值

维纳过程中的即时最大值${\displaystyle M_{t}=\max _{0\leq s\leq t}W_{s}}$与${\displaystyle W_{t}}$的联合概率分布是：

${\displaystyle f_{M_{t},W_{t}}(m,w)={\frac {2(2m-w)}{t{\sqrt {2\pi t}}}}e^{-{\frac {(2m-w)^{2}}{2t}}},m\geq 0,w\leq m}$

而即时最大值的分布${\displaystyle f_{M_{t}}}$是对${\displaystyle -\infty <w\leq m}$的积分：

${\displaystyle f_{M_{t}}(m)=\int _{-\infty }^{m}f_{M_{t},W_{t}}(m,w)\,dw=\int _{-\infty }^{m}{\frac {2(2m-w)}{t{\sqrt {2\pi t}}}}e^{-{\frac {(2m-w)^{2}}{2t}}}\,dw={\sqrt {\frac {2}{\pi t}}}e^{\frac {-m^{2}}{2t}}}$

即时最大值的数学期望是^[3]:114：

${\displaystyle \mathbb {E} M_{t}=\int _{0}^{\infty }mf_{M_{t}}(m)\,dm=\int _{0}^{\infty }m{\sqrt {\frac {2}{\pi t}}}e^{\frac {-m^{2}}{2t}}\,dm={\sqrt {\frac {2t}{\pi }}}.}$

由于维纳过程上下对称，即时最小值显然是即时最大值的相反数。

对称性质

将一个维纳过程不断按比例展开，它的一部分就会呈现另一个维纳过程的样子

• 尺度不变性：对任意的正实数${\displaystyle \alpha >0}$，随机过程${\displaystyle \left(V_{t}\right)_{t\geqslant 0}:\,\,V_{t}={\frac {1}{\sqrt {\alpha }}}W_{\alpha t}}$都仍然是一个维纳过程。
• 时间反转：对任意的正实数${\displaystyle T>0}$，随机过程${\displaystyle \left(V_{t}\right)_{0\leqslant t\leqslant T}:\,\,V_{t}=W_{T}-W_{T-t}}$和${\displaystyle \left(W_{t}\right)_{0\leqslant t\leqslant T}}$性质相同。
• 空间对称：随机过程${\displaystyle \left(V_{t}\right)_{t\geqslant 0}:\,\,V_{t}=-W_{t}}$也是一个维纳过程。
• 时间反演：随机过程${\displaystyle \left(V_{t}\right)_{t\geqslant 0}:\,\,V_{0}=0,\,\,\forall t>0,\,\,V_{t}=tW_{\frac {1}{t}}}$也是一个维纳过程。

参考资料：^[2]:13、^[4]:44

时间平移不变性和马尔可夫性质

维纳过程具有马尔可夫性质，也就是说，在任意一点之后的走势仅仅和这一点的取值相关，而与之前的取值无关。也就是说，对任何的有界连续函数${\displaystyle \phi }$，

${\displaystyle \mathbb {E} [\phi (W_{s},s\geqslant t)|{\mathcal {F}}_{t}]=\mathbb {E} [\phi (W_{s},s\geqslant t)|W_{t}]}$

因此维纳过程具有时间平移不变性：随机过程${\displaystyle \left(V_{t}\right)_{t\geqslant 0}:\,\,V_{t}=W_{t_{0}+t}-W_{t_{0}}}$也是一个维纳过程。不仅如此，维纳过程还满足强马尔可夫性质：对任意的有限停时${\displaystyle \tau }$，随机变量${\displaystyle B_{t}=W_{\tau +t}-W_{\tau }}$独立于滤波${\displaystyle {\mathcal {F}}_{\tau }}$。也就是说，对任何的有界连续函数${\displaystyle \phi }$，

${\displaystyle \mathbb {E} [\phi (W_{s},s\geqslant \tau )|{\mathcal {F}}_{\tau }]=\mathbb {E} [\phi (W_{s},s\geqslant \tau )|W_{\tau }].}$

维纳过程的强马尔可夫性质，说明即便给定的时间不是定时而是一个停时，维纳过程在停时之后的走势仍然与之前无关。所以，将停时之后的维纳过程上下反转，仍然会是一个维纳过程。用数学语言来说，就是：给定一个停时${\displaystyle \tau }$之后，随机变量：${\displaystyle B_{t}=W_{t}\mathbf {1} _{t\leqslant \tau }+\left(2W_{\tau }-W_{t}\right)\mathbf {1} _{t>\tau }}$也是一个维纳过程。这个性质也称为维纳过程的反射原理。

作为推论，可以建立即时最大值${\displaystyle M_{t}=\max _{0\leq s\leq t}W_{s}}$与${\displaystyle W_{t}}$的另一种关系。设有正实数${\displaystyle a>0}$停时${\displaystyle \tau _{a}=\inf\{t>0,\,W_{t}>a\}}$，那么${\displaystyle \{\tau _{a}\leqslant t\}=\{M_{t}\geqslant a\}}$。运用反射原理可以证明，${\displaystyle \mathbb {P} \left(M_{t}\geqslant a\right)=2\mathbb {P} \left(W_{t}\geqslant a\right)=\mathbb {P} \left(|W_{t}|\geqslant a\right)}$。更一般地，设有 ${\displaystyle a>b\geqslant 0}$，则${\displaystyle \mathbb {P} \left(W_{t}\leqslant b,\,M_{t}\geqslant a\right)=\mathbb {P} \left(W_{t}\geqslant 2a-b\right)}$。

参见

• 抽象维纳空间
• 经典维纳空间
• 切诺夫分布

参考来源

1. （英文）Rick Durrett. Probability: theory and examples,4th edition. Cambridge University Press. 2000. ISBN 0521765390.
2. （英文）Peter Mörters, Yuval Peres. Brownian Motion. Cambridge University Press Cambridge Series in Statistical and Probabilistic Mathematics. 2010. ISBN 9780521760188.
3. （英文）Steven E. Shreve. Stochastic Calculus for Finance II: Continuous Time Models. Springer. 2008. ISBN 978-0-387-40101-0.
4. Nizar Touzi, Peter Tankov. Calcul Stochastique en Finance. Les Éditions de l'École Polytechnique. 2010.

• Kleinert, Hagen, Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4th edition, World Scientific (Singapore, 2004); Paperback ISBN 981-238-107-4 (also available online: PDF-files （页面存档备份，存于互联网档案馆）)
• Stark,Henry, John W. Woods, Probability and Random Processes with Applications to Signal Processing, 3rd edition, Prentice Hall (New Jersey, 2002); Textbook ISBN 0-13-020071-9
• Daniel Revuz and Marc Yor, Continuous martingales and Brownian motion, second edition, Springer-Verlag 1994.