双三角锥柱

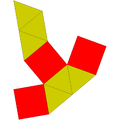
双三角锥柱是指以三角形为基底的双角锥柱，其可以由三角柱在两端各连接一个三角锥来构成。若双三角锥柱的基底为正三角形，且侧面都是正多边形的话，则这个立体是一种全部由正多边形组成的立体，为92种约翰逊多面体中的其中一个，其索引为J₁₄^[1]。约翰逊多面体是凸多面体，面皆由正多边形组成但不属于均匀多面体，共有92种。这些立体最早在1966年由诺曼·约翰逊（英语：Norman Johnson (mathematician)）（Norman Johnson）命名并给予描述^[2]。

双三角锥柱

类别	约翰逊多面体 J13 - J14 - J15
对偶多面体	双三角锥台
识别
名称	双三角锥柱
参考索引	J14
鲍尔斯缩写 （verse-and-dimensions的wikia：Bowers acronym）	etidpy
数学表示法
康威表示法	k3P3
性质
面	9
边	15
顶点	8
欧拉特征数	F=9, E=15, V=8 （χ=2）
组成与布局
面的种类	6个三角形 3个正方形
顶点图	2(33) 6(32.42)
对称性
对称群	D3h, [3,2], (*322)
图像
双三角锥台 （对偶多面体） （展开图）

nirrosula是一种由植物叶子条编织而成的非洲乐器，由一系列细长的双角锥柱制成，其端盖的面为不等边三角形，也就是非正的双三角锥柱外型的乐器。^[3]

性质

双三角锥柱共由9个面、15条边和8个顶点组成^[4][5][6]，在其9个面中，有6个三角形面和3个正方形面^[4]。在其8个顶点中，有两种顶点，一种顶点为3个三角形的公共顶点，在顶点图中可以用[3³]来表示^[7]，这种顶点有2个^[6]、另外一种顶点为2个三角形和2个正方形的公共顶点，在顶点图中可以用[3²,4²]来表示^[7]，这种顶点有6个^[6]。

体积与表面积

若一个双三角锥柱边长为${\displaystyle a}$，则其体积${\displaystyle V}$与表面积${\displaystyle A}$为：

${\displaystyle V=\left({\frac {1}{12}}\left(2{\sqrt {2}}+3{\sqrt {3}}\right)\right)\cdot a^{3}\approx 0.668715...a^{3}}$^[8][9]

${\displaystyle A=\left({\frac {3}{2}}\left(2+{\sqrt {3}}\right)\right)\cdot a^{2}\approx 5.59808...a^{2}}$^[8][9]

这样的双三角锥柱整体的高${\displaystyle H}$为：

${\displaystyle H={\frac {3+2{\sqrt {6}}}{3}}\cdot a\approx 2.63299...a}$^[9]

顶点坐标

若一个双三角锥柱边长为单位长，且几何中心位于原点，则其顶点坐标为：^[10]

${\displaystyle \left(\pm {\frac {1}{2}},\,-{\frac {\sqrt {3}}{6}},\,\pm {\frac {1}{2}}\right)}$

${\displaystyle \left(0,\,{\frac {\sqrt {3}}{3}},\,\pm {\frac {1}{2}}\right)}$

${\displaystyle \left(0,\,0,\,\pm {\frac {3+2{\sqrt {6}}}{6}}\right)}$

对偶多面体

主条目：双三角锥台

双三角锥柱的对偶多面体为双三角锥台，其由8个面组成，分别为6个梯形和2个三角形。^[11]

双三角锥柱的对偶多面体	对偶多面体的展开图

参见

• 约翰逊多面体
• 正多面体
• 正四面体
• 双三角锥