自然对数

自然对数（英语：Natural logarithm）为以数学常数e为底数的对数函数，标记作${\displaystyle \ln x}$或${\displaystyle \log _{e}x}$，其反函数为指数函数${\displaystyle e^{x}}$。^{[注 1]}

自然对数${\displaystyle \ln(x)}$的函数图像

自然对数${\displaystyle \ln(x)}$的积分定义

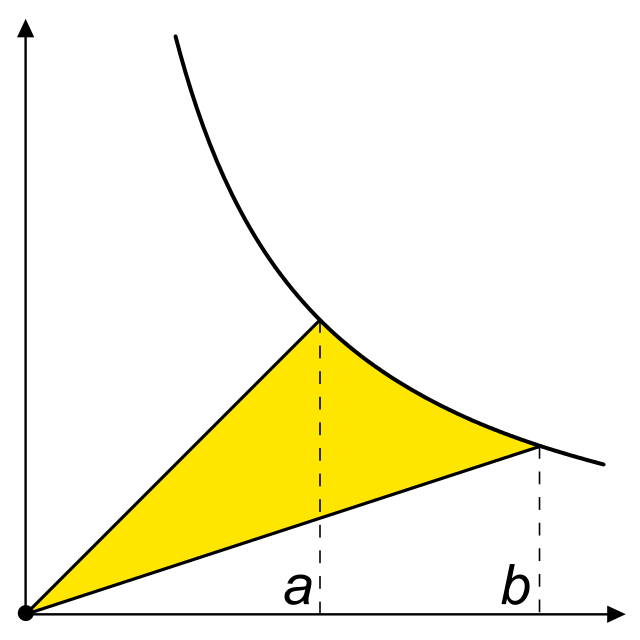
自然对数积分定义为对任何正实数${\displaystyle x}$，由${\displaystyle 1}$到${\displaystyle x}$所围成，${\displaystyle xy=1}$曲线下的面积。如果${\displaystyle x}$小于1，则计算面积为负数。

${\displaystyle \ln x=\int _{1}^{x}{\frac {dt}{t}}\,}$

${\displaystyle e}$则定义为唯一的实数${\displaystyle x}$使得${\displaystyle \ln x=1}$。

自然对数一般表示为${\displaystyle \ln x\!}$，数学中亦有以${\displaystyle \log x\!}$表示自然对数。^{[1][注 2]}

历史

十七世纪

双曲线扇形是笛卡尔平面${\displaystyle \{(x,y)\}}$上的一个区域，由从原点到${\textstyle (a,{\frac {1}{a}})}$和${\textstyle (b,{\frac {1}{b}})}$的射线，以及双曲线${\displaystyle xy=1}$围成。在标准位置的双曲线扇形有${\displaystyle a=1}$且${\displaystyle b>1}$，它的面积为${\displaystyle \ln(b)}$^[2]，此时双曲线扇形对应正双曲角。

当直角双曲线下的两段面积相等时，${\displaystyle x}$的值呈等比数列，${\textstyle {\frac {x_{2}}{x_{1}}}={\frac {x_{1}}{x_{0}}}=k}$，${\displaystyle y}$的值也呈等比数列，${\textstyle {\frac {x_{2}}{x_{1}}}={\frac {x_{1}}{x_{0}}}={\frac {1}{k}}}$。

约翰·纳皮尔在1614年^[3]以及约斯特·比尔吉在6年后^[4]，分别发表了独立编制的对数表，当时通过对接近1的底数的大量乘幂运算，来找到指定范围和精度的对数和所对应的真数。当时还没出现有理数幂的概念，按后世的观点，约翰·纳皮尔的底数0.9999999^10000000相当接近${\textstyle {\frac {1}{e}}}$^[5]，而约斯特·比尔吉的底数1.0001¹⁰⁰⁰⁰相当接近自然对数的底数${\displaystyle e}$。实际上不需要做开高次方这种艰难运算，约翰·纳皮尔用了20年时间进行相当于数百万次乘法的计算，亨利·布里格斯（英语：Henry Briggs (mathematician)）建议纳皮尔改用10为底数未果，他用自己的方法^[6]于1624年部分完成了常用对数表的编制。

形如${\displaystyle f(x)=x^{p}}$的曲线都有一个代数反导数，除了特殊情况${\displaystyle p=-1}$对应于双曲线的弓形面积（英语：Quadrature (mathematics)），即双曲线扇形；其他情况都由1635年发表的卡瓦列里弓形面积公式（英语：Cavalieri's quadrature formula）给出^[7]，其中抛物线的弓形面积由公元前3世纪的阿基米德完成（抛物线的弓形面积），双曲线的弓形面积需要发明一个新函数。1647年圣文森特的格列高利（英语：Grégoire de Saint-Vincent）将对数联系于双曲线${\displaystyle xy=1}$的弓形面积，他发现x轴上${\displaystyle [a,b]}$两点对应的双曲线线段与原点围成的双曲线扇形同${\displaystyle [c,d]}$对应的扇形，在${\textstyle {\frac {a}{b}}={\frac {c}{d}}}$时面积相同，这指出了双曲线从${\displaystyle x=1}$到${\displaystyle x=t}$的积分${\displaystyle f(t)}$满足^[8]：

${\displaystyle f(tu)=f(t)+f(u)\,}$

1649年，萨拉萨的阿尔丰斯·安东尼奥（英语：Alphonse Antonio de Sarasa）将双曲线下的面积解释为对数。大约1665年，伊萨克·牛顿推广了二项式定理，他将${\textstyle {\frac {1}{1+x}}}$展开并逐项积分，得到了自然对数的无穷级数。“自然对数”最早描述见于尼古拉斯·麦卡托在1668年出版的著作《Logarithmotechnia》中^[9]，他也独立发现了同样的级数，即自然对数的麦卡托级数。

十八世纪

大约1730年，欧拉定义互为逆函数的指数函数和自然对数为^[10][11]：

${\displaystyle e^{x}=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n},}$

${\displaystyle \ln(x)=\lim _{n\rightarrow \infty }n\left(x^{\frac {1}{n}}-1\right)}$

1742年威廉·琼斯发表了现在的幂指数概念^[12]。

形式定义

欧拉定义自然对数为序列的极限：

${\displaystyle \ln(x)=\lim _{n\rightarrow \infty }n\left(x^{\frac {1}{n}}-1\right).}$

${\displaystyle \ln(a)}$正式定义为积分，

${\displaystyle \ln(a)=\int _{1}^{a}{\frac {1}{x}}\,dx.}$

这个函数为对数是因满足对数的基本性质:

${\displaystyle \ln(ab)=\ln(a)+\ln(b).\,\!}$

这可以通过将定义了${\displaystyle \ln(ab)}$的积分拆分为两部分，并在第二部分中进行换元${\displaystyle x=ta}$来证实:

${\displaystyle \ln(ab)=\int _{1}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{a}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{1}^{b}{\frac {1}{at}}\;d(at)}$

${\displaystyle =\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{1}^{b}{\frac {1}{t}}\;dt=\ln(a)+\ln(b).}$

幂公式${\displaystyle \ln(t^{r})=r\ln(t)}$可如下推出:

${\displaystyle \ln(t^{r})=\int _{1}^{t^{r}}{\frac {1}{x}}dx=\int _{1}^{t}{\frac {1}{u^{r}}}d\left(u^{r}\right)=\int _{1}^{t}{\frac {1}{u^{r}}}\left(ru^{r-1}\,du\right)=r\int _{1}^{t}{\frac {1}{u}}\,du=r\ln(t).}$

第二个等式使用了换元${\displaystyle u=x^{\frac {1}{r}}}$。

自然对数还有在某些情况下更有用的另一个积分表示：

${\displaystyle \ln(x)=-\lim _{\epsilon \to 0}\int _{\epsilon }^{\infty }{\frac {dt}{t}}\left(e^{-xt}-e^{-t}\right).}$

性质

• ${\displaystyle \ln(1)=\int _{1}^{1}{\frac {1}{t}}\,dt=0\,}$
• ${\displaystyle \operatorname {ln} (-1)=i\pi \,}$

(参见复数对数)

• ${\displaystyle \ln(x)<\ln(y)\quad {\rm {for}}\quad 0<x<y\,}$
• ${\displaystyle \lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1\,}$
• ${\displaystyle \ln(x^{y})=y\,\ln(x)\,}$
• ${\displaystyle {\frac {x-1}{x}}\leq \ln(x)\leq x-1\quad {\rm {for}}\quad x>0\,}$
• ${\displaystyle \ln {(1+x^{\alpha })}\leq \alpha x\quad {\rm {for}}\quad x\geq 0,\alpha \geq 1\,}$

证明
${\displaystyle \lim _{h\to 0}{\frac {\ln(1+h)}{h}}=\lim _{h\to 0}{\frac {\ln(1+h)-\ln 1}{h}}={\frac {d}{dx}}\ln x{\Bigg |}_{x=1}=1}$

导数

自然对数的图像和它在${\displaystyle x=1.5}$处的切线。

${\displaystyle \ln(1+x)}$的泰勒多项式只在${\displaystyle -1<x\leq 1}$范围内有逐步精确的近似。

自然对数的导数为

${\displaystyle {\frac {d}{dx}}\ln(x)={\frac {1}{x}}.\,}$

证明一（微积分第一基本定理）:${\displaystyle {\frac {d}{dx}}\ln(x)={\frac {d}{dx}}\int _{1}^{x}{\frac {1}{t}}\,dt={\frac {1}{x}}}$

证明二：按此影片（页面存档备份，存于互联网档案馆）

${\displaystyle {\frac {d}{dx}}\ln(x)=\lim _{h\to 0}{\frac {\ln(x+h)-\ln(x)}{h}}}$

${\displaystyle =\lim _{h\to 0}{\frac {\ln({\frac {x+h}{x}})}{h}}}$

${\displaystyle =\lim _{h\to 0}\left[{\frac {1}{h}}\ln \left(1+{\frac {h}{x}}\right)\right]\quad }$

${\displaystyle =\lim _{h\to 0}\ln \left(1+{\frac {h}{x}}\right)^{\frac {1}{h}}}$

设${\displaystyle u={\frac {h}{x}}\Rightarrow ux=h}$

${\displaystyle {\frac {1}{h}}={\frac {1}{ux}}}$

${\displaystyle {\frac {d}{dx}}\ln(x)=\lim _{u\to 0}\ln(1+u)^{\frac {1}{ux}}}$

${\displaystyle =\lim _{u\to 0}\ln \left[(1+u)^{\frac {1}{u}}\right]^{\frac {1}{x}}}$

${\displaystyle ={\frac {1}{x}}\lim _{u\to 0}\ln(1+u)^{\frac {1}{u}}}$

设${\displaystyle n={\frac {1}{u}}\Rightarrow u={\frac {1}{n}}}$

${\displaystyle {\frac {d}{dx}}\ln(x)={\frac {1}{x}}\lim _{n\to \infty }\ln \left(1+{\frac {1}{n}}\right)^{n}}$

${\displaystyle ={\frac {1}{x}}\ln \left[\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}\right]}$

${\displaystyle ={\frac {1}{x}}\ln e}$

${\displaystyle ={\frac {1}{x}}}$

用自然对数定义的更一般的对数函数，${\displaystyle \log _{b}(x)={\frac {\ln(x)}{\ln(b)}}}$，根据其逆函数即一般指数函数的性质，它的导数为^[13][14]：

${\displaystyle {\frac {d}{dx}}\log _{b}(x)={\frac {1}{x\ln(b)}}.}$

根据链式法则，以${\displaystyle f(x)}$为参数的自然对数的导数为

${\displaystyle {\frac {d}{dx}}\ln[f(x)]={\frac {f'(x)}{f(x)}}.}$

右手端的商叫做${\displaystyle f}$的对数导数（英语：logarithmic derivative），通过${\displaystyle \ln(f(x))}$的导数的方法计算${\displaystyle f'(x)}$叫做对数微分^[15]。

幂级数

自然对数的导数性质导致了${\displaystyle \ln(1+x)}$在0处的泰勒级数，也叫做麦卡托级数：

${\displaystyle \ln(1+x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots }$

对于所有${\displaystyle \left|x\right|\leq 1,}$但不包括${\displaystyle x=-1.}$

把${\displaystyle x-1}$代入${\displaystyle x}$中，可得到${\displaystyle \ln(x)}$自身的级数。通过在麦卡托级数上使用欧拉变换，可以得到对绝对值大于1的任何${\displaystyle x}$有效的如下级数:

${\displaystyle \ln {x \over {x-1}}=\sum _{n=1}^{\infty }{1 \over {nx^{n}}}={1 \over x}+{1 \over {2x^{2}}}+{1 \over {3x^{3}}}+\cdots \,.}$

这个级数类似于贝利-波尔温-普劳夫公式。

还要注意到${\displaystyle x \over {x-1}}$是自身的逆函数，所以要生成特定数${\displaystyle y}$的自然对数，简单把${\displaystyle x \over {x-1}}$代入${\displaystyle x}$中。

${\displaystyle \ln {x}=\sum _{n=1}^{\infty }{1 \over {n}}\left({x-1 \over x}\right)^{n}=\left({x-1 \over x}\right)+{1 \over 2}\left({x-1 \over x}\right)^{2}+{1 \over 3}\left({x-1 \over x}\right)^{3}+\cdots \,}$

对于${\displaystyle \operatorname {Re} (x)\geq {\frac {1}{2}}\,.}$

自然数的倒数的总和

${\displaystyle 1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}},}$

叫做调和级数。它与自然对数有密切联系：当${\displaystyle n}$趋于无穷的时候，差

${\displaystyle \sum _{k=1}^{n}{\frac {1}{k}}-\ln(n),}$

收敛于欧拉-马歇罗尼常数。这个关系有助于分析算法比如快速排序的性能。^[16]

积分

自然对数通过分部积分法积分:

${\displaystyle \int \ln(x)\,dx=x\ln(x)-x+C.}$

假设:

${\displaystyle u=\ln(x)\Rightarrow du={\frac {dx}{x}}}$

${\displaystyle dv=dx\Rightarrow v=x\,}$

所以:

${\displaystyle {\begin{aligned}\int \ln(x)\,dx&=x\ln(x)-\int {\frac {x}{x}}\,dx\\&=x\ln(x)-\int 1\,dx\\&=x\ln(x)-x+C\end{aligned}}}$

自然对数可以简化形如${\displaystyle g(x)={\frac {f'(x)}{f(x)}}}$的函数的积分：${\displaystyle g(x)}$的一个原函数给出为${\displaystyle \ln(\left\vert f(x)\right\vert )}$。这是基于链式法则和如下事实:

${\displaystyle \ {d \over dx}\ln \left|x\right|={1 \over x}.}$

换句话说，

${\displaystyle \int {1 \over x}dx=\ln |x|+C}$

且

${\displaystyle \int {{\frac {f'(x)}{f(x)}}\,dx}=\ln |f(x)|+C.}$

例子

下面是${\displaystyle g(x)=\tan x}$的例子：

${\displaystyle {\begin{aligned}\int \tan x\,dx&=\int {\sin x \over \cos x}\,dx\\&=\int {-{d \over dx}\cos x \over {\cos x}}\,dx.\\\end{aligned}}}$

设${\displaystyle f(x)=\cos x}$且${\displaystyle f'(x)=-\sin x}$：

${\displaystyle {\begin{aligned}\int \tan x\,dx&=-\ln {\left|\cos x\right|}+C\\&=\ln {\left|\sec x\right|}+C\\\end{aligned}}}$

与双曲函数的关系

在直角双曲线(方程${\displaystyle y={\frac {1}{x}}}$)下，双曲线三角形(黄色)，和对应于双曲角${\displaystyle u}$的双曲线扇形(红色)。这个三角形的边分别是双曲函数中${\displaystyle \cosh }$和${\displaystyle \sinh }$的${\displaystyle {\sqrt {2}}}$倍。

射线出原点交单位双曲线${\displaystyle \scriptstyle x^{2}\ -\ y^{2}\ =\ 1}$于点${\displaystyle \scriptstyle (\cosh \,a,\,\sinh \,a)}$，这里的${\displaystyle \scriptstyle a}$是射线、双曲线和${\displaystyle \scriptstyle x}$轴围成的面积的二倍。对于双曲线上位于x轴下方的点，这个面积被认为是负值。

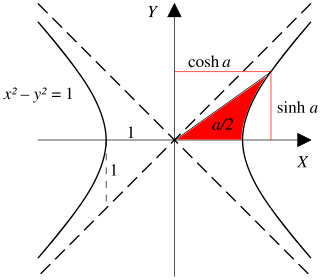
在18世纪，约翰·海因里希·兰伯特介入双曲函数^[17]，并计算双曲几何中双曲三角形的面积^[18]。对数函数是在直角双曲线${\displaystyle xy=1}$下定义的，可构造双曲线直角三角形，底边在线${\displaystyle y=x}$上，一个顶点是原点，另一个顶点在双曲线。这里以自然对数即双曲角作为参数的函数，是自然对数的逆函数指数函数，即要形成指定双曲角${\displaystyle u}$，在渐近线即x或y轴上需要有的${\displaystyle x}$或${\displaystyle y}$的值。显见这里的底边是${\displaystyle \left(e^{u}+e^{-u}\right){\frac {\sqrt {2}}{2}}}$，垂线是${\displaystyle \left(e^{u}-e^{-u}\right){\frac {\sqrt {2}}{2}}}$。

通过旋转和缩小线性变换，得到单位双曲线下的情况，有：

• ${\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}}$
• ${\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}}$

单位双曲线中双曲线扇形的面积是对应直角双曲线${\displaystyle xy=1}$下双曲角的${\displaystyle {\frac {1}{2}}}$。

连分数

尽管自然对数没有简单的连分数，但有一些广义连分数如:

${\displaystyle {\begin{aligned}\ln(1+x)&={\frac {x^{1}}{1}}-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+{\frac {x^{5}}{5}}-\cdots \\&={\cfrac {x}{1-0x+{\cfrac {1^{2}x}{2-1x+{\cfrac {2^{2}x}{3-2x+{\cfrac {3^{2}x}{4-3x+{\cfrac {4^{2}x}{5-4x+\ddots }}}}}}}}}}\\\end{aligned}}}$

${\displaystyle {\begin{aligned}\ln \left(1+{\frac {x}{y}}\right)&={\cfrac {x}{y+{\cfrac {1x}{2+{\cfrac {1x}{3y+{\cfrac {2x}{2+{\cfrac {2x}{5y+{\cfrac {3x}{2+\ddots }}}}}}}}}}}}\\&={\cfrac {2x}{2y+x-{\cfrac {(1x)^{2}}{3(2y+x)-{\cfrac {(2x)^{2}}{5(2y+x)-{\cfrac {(3x)^{2}}{7(2y+x)-\ddots }}}}}}}}\\\end{aligned}}}$

这些连分数特别是最后一个对接近1的值快速收敛。但是，更大的数的自然对数，可以轻易的用这些更小的数的自然对数的加法来计算，带有类似的快速收敛。

例如，因为${\displaystyle 2=1.25^{3}\times 1.024}$，2的自然对数可以计算为:

${\displaystyle {\begin{aligned}\ln 2&=3\ln \left(1+{\frac {1}{4}}\right)+\ln \left(1+{\frac {3}{125}}\right)\\&={\cfrac {6}{9-{\cfrac {1^{2}}{27-{\cfrac {2^{2}}{45-{\cfrac {3^{2}}{63-\ddots }}}}}}}}+{\cfrac {6}{253-{\cfrac {3^{2}}{759-{\cfrac {6^{2}}{1265-{\cfrac {9^{2}}{1771-\ddots }}}}}}}}.\\\end{aligned}}}$

进而，因为${\displaystyle 10=1.25^{10}\times 1.024^{3}}$，10的自然对数可以计算为:

${\displaystyle {\begin{aligned}\ln 10&=10\ln \left(1+{\frac {1}{4}}\right)+3\ln \left(1+{\frac {3}{125}}\right)\\&={\cfrac {20}{9-{\cfrac {1^{2}}{27-{\cfrac {2^{2}}{45-{\cfrac {3^{2}}{63-\ddots }}}}}}}}+{\cfrac {18}{253-{\cfrac {3^{2}}{759-{\cfrac {6^{2}}{1265-{\cfrac {9^{2}}{1771-\ddots }}}}}}}}.\\\end{aligned}}}$

复数对数

主条目：复数对数

指数函数可以扩展为对任何复数${\displaystyle x}$得出复数值为${\displaystyle e^{x}}$的函数，只需要简单使用${\displaystyle x}$为复数的无穷级数；这个指数函数的逆函数形成复数对数，并带有正常的对数的多数性质。但是它涉及到了两个困难：不存在${\displaystyle x}$使得${\displaystyle e^{x}=0}$；并且有着${\displaystyle e^{2\pi i}=1=e^{0}}$。因为乘法性质仍适用于复数指数函数，${\displaystyle e^{z}=e^{z+2n\pi i}}$，对于所有复数${\displaystyle z}$和整数${\displaystyle n}$。

所以对数不能定义在整个复平面上，并且它是多值函数，就是说任何复数对数都可以增加${\displaystyle 2\pi i}$的任何整数倍而成为等价的对数。复数对数只能在切割平面上是单值函数。例如，${\displaystyle \log i={\frac {1}{2}}\pi i}$或${\displaystyle {\frac {5}{2}}\pi i}$或${\displaystyle -{\frac {3}{2}}\pi i}$等等；尽管${\displaystyle i^{4}=1}$，${\displaystyle 4\log =i}$不能定义为${\displaystyle 2\pi i}$或${\displaystyle 10\pi i}$或${\displaystyle -6\pi i}$，以此类推。

• 自然对数函数在复平面（主分支）上的绘图
• 
  z=Re(ln(x+iy))
• 
• 
• 
  前三图的叠加

主值定义

对于每个非0复数${\displaystyle z=x+yi}$，主值${\displaystyle \log z}$是虚部位于区间${\displaystyle (-\pi ,\pi ]}$内的对数。表达式${\displaystyle \log 0}$不做定义，因为没有复数${\displaystyle w}$满足${\displaystyle e^{w}=0}$。

要对${\displaystyle \log z}$给出一个公式，可以先将${\displaystyle z}$表达为极坐标形式，${\displaystyle z=re^{i\theta }}$。给定${\displaystyle z}$，极坐标形式不是确切唯一的，因为有可能向${\displaystyle \theta }$增加${\displaystyle 2\pi }$的整数倍，所以为了保证唯一性而要求${\displaystyle \theta }$位于区间${\displaystyle (-\pi ,\pi ]}$内；这个${\displaystyle \theta }$叫做幅角的主值，有时写为${\displaystyle \operatorname {arg} z}$或${\displaystyle \operatorname {atan} 2(y,x)}$。则对数的主值可以定义为^[19] ：

${\displaystyle \operatorname {Log} z:={\text{ln }}r+i\theta =\ln |z|+i\operatorname {Arg} z=\operatorname {ln} {\sqrt {x^{2}+y^{2}}}+i\operatorname {atan2} (y,x).}$

例如，${\displaystyle \operatorname {Log} (-3i)=\ln 3-{\frac {\pi i}{2}}}$。

科学应用

自然指数有应用于表达放射衰变（放射性）之类关于衰减的过程，如放射性原子数目的微分方程${\displaystyle N}$随时间变化率${\displaystyle {\frac {dN}{dt}}=-pN}$，常数${\displaystyle p}$为原子衰变概率，积分得${\displaystyle N(t)=N(0)\exp(-pt)}$。

注释

1. 根据微积分学，某函数之定义域为其反函数之值域，反之其值域为其反函数之定义域。因${\displaystyle e^{x}}$的值域为${\displaystyle (0,\infty )}$，且其为${\displaystyle \ln x}$之反函数，故可知${\displaystyle \ln x}$之定义域为${\displaystyle (0,\infty )}$，即${\displaystyle \ln x}$在非正实数系无法定义。
2. 若要避免与底为10的常用对数 ${\displaystyle \log x\!}$ 混淆，可用“全写” ${\displaystyle \log _{\boldsymbol {e}}x\!}$ 。

参考资料

1. 例如哈代和赖特所著的《数论入门》"Introduction to the theory of numbers" (1.7, Sixth edition, Oxford 2008)的注解 "log x is, of course the 'Napierian' logarithm of x, to base e. 'Common' logarithms have no mathematical interest."（log x 当然是以e为基，x的“纳皮尔”对数。“常用”对数在数学上毫无重要。）
2. 证明：从1到b积分1/x，增加三角形{(0, 0), (1, 0), (1, 1)}，并减去三角形{(0, 0), (b, 0), (b, 1/b)}。
3. Ernest William Hobson, John Napier and the invention of logarithms, 1614, Cambridge: The University Press, 1914
4. Boyer, Carl B., 14，Section "Jobst Bürgi", A History of Mathematics, New York: John Wiley & Sons, 1991, ISBN 978-0-471-54397-8
5. 选取接近e的底数b，对数表涉及的b^x为单调增函数，定义域为0到1而值域为1到b；选取接近1/e的底数b，对数表涉及的b^x为单调减函数，定义域为0到∞而值域为1到0。
6. 以${\displaystyle 10^{\frac {1}{2^{54}}}}$这个接近1的数为基础。
7. 博纳文图拉·卡瓦列里在1635年的《Geometria indivisibilibus continuorum nova quadam ratione promota》中给出定积分：

   ${\displaystyle \int _{0}^{a}x^{n}\,dx={\tfrac {1}{n+1}}\,a^{n+1}\qquad n\geq 0,}$

   其不定积分形式为：

   ${\displaystyle \int x^{n}\,dx={\tfrac {1}{n+1}}\,x^{n+1}+C\qquad n\neq -1.}$

   独立发现者还有：皮埃尔·德·费马、罗贝瓦尔的吉尔（英语：Gilles de Roberval）和埃万杰利斯塔·托里拆利。
8. 设a=1，x轴上[a,b]两点对应的双曲线线段与原点围成的双曲线扇形面积为f(b)，[c,d]对应的扇形面积为f(d)-f(c)，d=bc，即为f(bc)-f(c)，当且仅当f(bc)=f(b)+f(c)时，两双曲线扇形面积相等。
9. J. J. O'Connor; E. F. Robertson, The number e, The MacTutor History of Mathematics archive, September 2001 [2009-02-02], （原始内容存档于2012-02-19）
10. 卡瓦列里弓形面积公式，对于负数值的n(x的负数幂)，由于在x = 0处有个奇点，因此定积分的下限为1，而不是0，即为：

    ${\displaystyle \int _{1}^{a}x^{n}\,dx={\tfrac {1}{n+1}}(a^{n+1}-1)\qquad n\neq -1.}$

    欧拉的自然对数定义：

    ${\displaystyle {\begin{aligned}\ln(x)&=\lim _{n\rightarrow \infty }n(x^{1/n}-1)\\&=\lim _{n\rightarrow -1}{\tfrac {1}{n+1}}(x^{n+1}-1)\\\end{aligned}}}$

11. Maor, Eli, e: The Story of a Number, Princeton University Press, 2009, ISBN 978-0-691-14134-3,sections 1, 1.
    Eves, Howard Whitley, An introduction to the history of mathematics, The Saunders series 6th, Philadelphia: Saunders, 1992, ISBN 978-0-03-029558-4, section 9-3
    Boyer, Carl B., A History of Mathematics, New York: John Wiley & Sons, 1991, ISBN 978-0-471-54397-8, p. 484, 489
12. ${\displaystyle \left(1+{\frac {1}{n}}\right)^{x}=\left(\left(1+{\frac {1}{n}}\right)^{n}\right)^{\frac {x}{n}}}$
    在最初的概念下，底数是接近1的数，而对数是整数；经过简单变换后，底数变大了，成为接近数学常量e的数，而对数变小了，成为 x/n。
13. Lang 1997, section IV.2
14. Wolfram, Stephen. "Calculation of d/dx(Log(b,x))". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research. （原始内容存档于2011-07-18） （英语）.
15. Kline, Morris, Calculus: an intuitive and physical approach, Dover books on mathematics, New York: Dover Publications, 1998, ISBN 978-0-486-40453-0, p. 386
16. Havil, Julian, Gamma: Exploring Euler's Constant, Princeton University Press, 2003, ISBN 978-0-691-09983-5, sections 11.5 and 13.8
17. Eves, Howard, Foundations and Fundamental Concepts of Mathematics, Courier Dover Publications: 59, 2012, ISBN 9780486132204, We also owe to Lambert the first systematic development of the theory of hyperbolic functions and, indeed, our present notation for these functions.
18. Ratcliffe, John, Foundations of Hyperbolic Manifolds, Graduate Texts in Mathematics 149, Springer: 99, 2006 [2014-03-28], ISBN 9780387331973, （原始内容存档于2014-01-12）, That the area of a hyperbolic triangle is proportional to its angle defect first appeared in Lambert's monograph Theorie der Parallellinien, which was published posthumously in 1786.
19. Sarason, Section IV.9.

延伸阅读

• John B. Conway, Functions of one complex variable, 2nd edition, Springer, 1978.
• Serge Lang, Complex analysis, 3rd edition, Springer-Verlag, 1993.
• Gino Moretti, Functions of a Complex Variable, Prentice-Hall, Inc., 1964.
• Donald Sarason, Complex function theory （页面存档备份，存于互联网档案馆）, 2nd edition, American Mathematical Society, 2007.
• E. T. Whittaker（英语：E. T. Whittaker） and G. N. Watson, A Course in Modern Analysis, fourth edition, Cambridge University Press, 1927.