直言三段论

直言三段论是所有前提都是直言命题的演绎推理。前两个命题被分别称为大前提和小前提^[1]。如果这个三段论是有效的，这两个前提逻辑上蕴涵了最后的命题，它叫做结论。结论的真实性建立在前提的真实性和它们之间的联系之上：中项在前提中必须周延（distribute）至少一次，形成在结论中的主词和谓词之间的连接。例如：

所有生物都会死。

所有人都是生物。

所以，所有人都会死。

这里的中项“生物”在大前提中周延，大项“会死者”在大前提和结论中都不周延，小项“人”在小前提和结论中周延；这个三段论符合周延规则：中项至少在一个前提中周延。一些直言三段论不是有效的，例如：

所有鸟都有翅膀。

所有人都不是鸟。

所以，没有人有翅膀。

即使此例子的两个前提和结论都是正确的，中项“鸟”在大前提和小前提中周延，大项“有翅膀”在结论中周延，小项“人”在小前提和结论中周延；此三段论却是一种大项不当谬误，将结论“没有人有翅膀”理解为同样表达的“所有人没有翅膀”如此一来方便了解其中的谬误；此三段论不有效的原因是它不符合另一个周延规则：在结论中周延的词项，在前提中也必须周延。在该三段论中大项“有翅膀”在结论被否定了，也就是说表达了人没有“有翅膀”，大项在此周延，但在大前提中未周延，因为在大前提中“有翅膀”并没有涉及该项的所有个体。

语气和格式

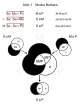
对立四边形图，揭示传统逻辑四种命题语气的关系，红色表示非空，黑色表示空。

三段论有如下典型形式：

大前提：所有M是P。

小前提：所有S是M。

结论：所有S是P。

其中S代表结论的主词（Subject），P代表结论的谓词（Predicate），M代表中词（Middle）。

三段论的命题可分为全称（universal）、特称（particular），及肯定、否定，组合起来有以下四类语气（Mood）：

类型	代号	形式	范例
全称肯定型	A（SaP）	所有S是P	所有人是会死的
全称否定型	E（SeP）	没有S是P	没有人是完美的
特称肯定型	I（SiP）	有些S是P	有些人是健康的
特称否定型	O（SoP）	有些S不是P	有些人不是健康的

三段论中，结论中的谓词称作大词（P，或称大项），包含大词在内的前提称作大前提；结论中的主词称作小词（S，或称小项），包含小词在内的前提称作小前提；没有出现在结论，却在两个前提重复出现的称作中词（M，或称中项）。大词、中词、小词依不同排列方式，可分成四种格（Figure）：

	第1格	第2格	第3格	第4格
大前提	M-P	P-M	M-P	P-M
小前提	S-M	S-M	M-S	M-S
结论	S-P	S-P	S-P	S-P

将以上整合在一起，三段论的大前提、小前提、结论分别可为A、E、I、O型命题之一，又可分为4格，故总共有256种三段论（若考虑大前提与小前提对调，便有512种，但逻辑上是相同的）。

三段论依语气与格的分类缩写，例如AAA-1（也可以写成1-AAA）代表“大前提为A型，小前提为A型，结论为A型，第1格”的三段论。

此外，三段论的四种格之间可相互转换：

• 第1格：对换大前提的主词和谓词的位置就变成第2格，对换小前提的主词和谓词的位置就变成第3格。
• 第2格：对换大前提的主词和谓词的位置就变成第1格，对换小前提的主词和谓词的位置就变成第4格。
• 第3格：对换大前提的主词和谓词的位置就变成第4格，对换小前提的主词和谓词的位置就变成第1格。
• 第4格：对换大前提的主词和谓词的位置就变成第3格，对换小前提的主词和谓词的位置就变成第2格。

E和I命题对换主词和谓词的位置而保持同原命题等价。A命题和O命题不能对换主词和谓词的位置，但是可以采用直接推理中的“对置法”。A命题还可以在确实主词有元素存在的前提下，转换成弱于原命题的I命题后再对换主词和谓词的位置。

有效性

考虑各种直言三段论的有效性将是非常冗长耗时的。前人想出了三个可供选择的方法来找出有效性。方法之一是记住下一章节中列出的所有论式。

还可以通过构造文氏图的方法得到有效形式。因为有三种项，文氏图需要三个交叠的圆圈来表示每一个类。首先，为小项构造一个圆圈。临近小项的圆圈的是同小项有着交叠的大项的圆圈。在这两个圆圈之上是中项的圆圈。它应当在三个位置有着交叠：大项，小项和大项与小项交叠的地方。一个三段论是有效的，其必然条件是通过图解两个前提得出结论的真实性。永不图解结论，因为结论必须从前提推导出来。总是首先图解全称命题。这是通过对一个类在另一个类中没有成员的区域加黑影来实现的。所以在前面例子的AAA-1形式中大前提“所有M是P”中，对M不与P交叠的所有区域加黑影，包括M与S交叠的部分。接着对小前提重复同样的过程。从这两个前提中可推导出在类S中所有成员也是类P的成员。但是，不能推出类P的所有成员都是类S的成员。

作为文氏图方法的另一个例子，考虑形式EIO-1的三段论。它的大前提是“没有M是P”，它的小前提是“有些S是M”，它的结论是“有些S不是P”。这个三段论的大项是P，它的小项是S，它的中项是M。大前提在图中通过对交集M ∩ P加阴影表示。小前提不能通过对任何区域加黑影表示。转而，我们可以在交集S ∩ M的非黑影部分使用x符号来表示“有些S是M”。（注意：黑影区域和存在量化区域是互斥的）。接着因为存在符号位于S内但在P外，所以结论“存在一些S不是P”是正确的。

本文最后一节列出了所有24个有效论式的文氏图。

最后一种方法是记住下面非形式表述的几条规则以避免谬论。尽管文氏图对于诠释目的是好工具，有人更喜欢用这些规则来检验有效性。

基本规则：

1. 结论中周延的词必须在前提中周延（谬误：大词不当、小词不当）。
2. 中词必须周延至少一次（谬误：中词不周延）。
3. 结论中否定命题的数目必须和前提中否定命题的数目相等：
   1. 二前提皆肯定，则结论必须为肯定（谬误：肯定前提推得否定结论）。
   2. 一前提是否定，则结论必须为否定（谬误：否定前提推得肯定结论）。
   3. 二前提皆否定，则三段论必无效（谬误：排它前提谬误）。
4. 结论中特称命题的数目必须和前提中特称命题的数目相等：
   1. 二前提皆全称，则结论必须为全称。
   2. 一前提是特称，则结论必须为特称。
   3. 二前提皆特称，则三段论必无效。

若一个三段论式满足以上的所有规则，就必定有效。

其他检查：

• 如果语境上不能假设所有提及的集合非空，部分推论将会无效（谬误：存在谬误）。
• 必须包含严格的三个词，不多不少。且须注意所有关键词和结构的语义是否一致（谬误：四词谬误、歧义谬误）。

有效三段论式

唯有第一格的所有有效三段论式的结论涵盖了A、E、I、O全部四种命题，第二格的所有有效三段论式皆为否定结论（E或O），第三格的所有有效三段论式皆为特称结论（I或O），第四格的所有有效三段论式皆为否定结论或特称结论（E、I或O）。下面表格中加下划线者必须假设所有提及的集合非空才有效。

第1格	第2格	第3格	第4格
AAA	AEE	AAI	AAI
EAE	EAE	EAO	EAO
AII	AOO	AII	AEE
EIO	EIO	EIO	EIO
AAI	AEO	IAI	IAI
EAO	EAO	OAO	AEO

在全部256种三段论式中，有24种有效，但是如果不能确定所有提及的集合为非空，则只有15种有效。

常犯的无效三段论式

1-AEE, 1-AEO, 1-EEA, 1-EEE, 1-EEI, 1-AIA, 1-IAA, 1-IAI, 1-III, 1-AOO, 1-OAO, 1-IEO
2-AAA, 2-AAI, 2-AII, 2-IAI, 2-OAO, 2-IEO, 2-EOI, 2-OEI, 2-IOO, 2-OIO
3-AAA, 3-AEE, 3-EAE, 3-AEO, 3-AOO, 3-AIA, 3-IAA, 3-III, 3-EOI, 3-OEI, 3-IEO
4-AAA, 4-EAE, 4-AII, 4-IEO

三段论式列表

总共有19个有效的论式，算结论弱化（全称弱化为特称）的5个论式则为24个有效论式，其中每一格刚好各有6个有效论式。为便于记忆，中世纪的学者将这些有效论式分别取了对应的拉丁语名字，每个名字的加了下划线的元音即是对应的语气：

第1格	第2格	第3格	第4格
Barbara	Camestres	Darapti	Bamalip
Celarent	Cesare	Felapton	Fesapo
Darii	Baroco	Datisi	Calemes
Ferio	Festino	Ferison	Fresison
Barbari	Camestros	Disamis	Dimaris
Celaront	Cesaro	Bocardo	Calemos

经典三段论式

下面列出的是亚里士多德的《前分析篇》中关于前3个格的14个三段论式。

第1格

• AAA（Barbara）

 所有M是P。
 所有S是M。
∴所有S是P。

${\displaystyle {\cfrac {\forall x(M(x)\rightarrow P(x))\qquad \forall x(S(x)\rightarrow M(x))}{\forall x(S(x)\rightarrow P(x))}}}$

• EAE（Celarent）

 没有M是P。
 所有S是M。
∴没有S是P。

${\displaystyle {\cfrac {\forall x(M(x)\rightarrow \lnot P(x))\quad \forall x(S(x)\rightarrow M(x))}{\forall x(S(x)\rightarrow \lnot P(x))}}}$

• AII（Darii）

 所有M是P。
 有些S是M。
∴有些S是P。

${\displaystyle {\cfrac {\forall x(M(x)\rightarrow P(x))\qquad \exists x(S(x)\land M(x))}{\exists x(S(x)\land P(x))}}}$

• EIO（Ferio）

 没有M是P。
 有些S是M。
∴有些S不是P。

${\displaystyle {\cfrac {\forall x(M(x)\rightarrow \lnot P(x))\quad \exists x(S(x)\land M(x))}{\exists x(S(x)\land \lnot P(x))}}}$

第2格

• AEE（Camestres）

 所有P是M。
 没有S是M。
∴没有S是P。

${\displaystyle {\cfrac {\cfrac {{\begin{matrix}\quad \\\forall x(P(x)\rightarrow M(x))\end{matrix}}\qquad {\cfrac {\forall x(S(x)\rightarrow \lnot M(x))}{\forall x(M(x)\rightarrow \lnot S(x))}}}{\forall x(M(x)\rightarrow \lnot S(x))\qquad \forall x(P(x)\rightarrow M(x))}}{\cfrac {\forall x(P(x)\rightarrow \lnot S(x))}{\forall x(S(x)\rightarrow \lnot P(x))}}}}$

（AEE-2是AEE-4的等价形式。这种形式还有其他推导方法。）^[2]

• EAE（Cesare）

 没有P是M。
 所有S是M。
∴没有S是P。

${\displaystyle {\cfrac {{\cfrac {\forall x(P(x)\rightarrow \lnot M(x))}{\forall x(M(x)\rightarrow \lnot P(x))}}\qquad {\begin{matrix}\quad \\\forall x(S(x)\rightarrow M(x))\end{matrix}}}{\forall x(S(x)\rightarrow \lnot P(x))}}}$

（EAE-2是EAE-1的等价形式。）

• AOO（Baroco）

 所有P是M。
 有些S不是M。
∴有些S不是P。

${\displaystyle {\cfrac {{\cfrac {\cfrac {\forall x(P(x)\rightarrow M(x))}{\forall x(P(x)\rightarrow \lnot (\lnot M(x)))}}{\forall x((\lnot M(x))\rightarrow \lnot P(x))}}\quad {\cfrac {\exists x(S(x)\land \lnot M(x))}{\exists x(S(x)\land (\lnot M(x)))}}}{\exists x(S(x)\land \lnot P(x))}}}$

（这种形式还有其他推导方法。）^[3]

• EIO（Festino）

 没有P是M。
 有些S是M。
∴有些S不是P。

${\displaystyle {\cfrac {{\cfrac {\forall x(P(x)\rightarrow \lnot M(x))}{\forall x(M(x)\rightarrow \lnot P(x))}}\qquad {\begin{matrix}\quad \\\exists x(S(x)\land M(x))\end{matrix}}}{\exists x(S(x)\land \lnot P(x))}}}$

（EIO-2是EIO-1的等价形式。）

第3格

• AAI（Darapti）

 所有M是P。
 所有M是S。
∴有些S是P。
（这种形式需要假定有些M确实存在。）^[4]

${\displaystyle {\cfrac {{\begin{matrix}\quad \\\quad \\\quad \\\forall x(M(x)\rightarrow P(x))\end{matrix}}\ {\cfrac {{\begin{matrix}\quad \\\forall x(M(x)\rightarrow S(x))\end{matrix}}\quad {\cfrac {\exists xM(x)}{\exists x(M(x)\land M(x))}}}{\cfrac {\exists x(M(x)\land S(x))}{\exists x(S(x)\land M(x))}}}}{\exists x(S(x)\land P(x))}}}$

• EAO（Felapton）

 没有M是P。
 所有M是S。
∴有些S不是P。
（这种形式需要假定有些M确实存在。）^[5]

${\displaystyle {\cfrac {{\begin{matrix}\quad \\\quad \\\quad \\\forall x(M(x)\rightarrow \lnot P(x))\end{matrix}}\,{\cfrac {{\begin{matrix}\quad \\\forall x(M(x)\rightarrow S(x))\end{matrix}}\quad {\cfrac {\exists xM(x)}{\exists x(M(x)\land M(x))}}}{\cfrac {\exists x(M(x)\land S(x))}{\exists x(S(x)\land M(x))}}}}{\exists x(S(x)\land \lnot P(x))}}}$

• AII（Datisi）

 所有M是P。
 有些M是S。
∴有些S是P。

${\displaystyle {\cfrac {{\begin{matrix}\quad \\\forall x(M(x)\rightarrow P(x))\end{matrix}}\qquad {\cfrac {\exists x(M(x)\land S(x))}{\exists x(S(x)\land M(x))}}}{\exists x(S(x)\land P(x))}}}$

（AII-3是AII-1的等价形式。）

• EIO（Ferison）

 没有M是P。
 有些M是S。
∴有些S不是P。

${\displaystyle {\cfrac {{\begin{matrix}\quad \\\forall x(M(x)\rightarrow \lnot P(x))\end{matrix}}\quad {\cfrac {\exists x(M(x)\land S(x))}{\exists x(S(x)\land M(x))}}}{\exists x(S(x)\land \lnot P(x))}}}$

（EIO-3是EIO-1的等价形式。）

• IAI（Disamis）

 有些M是P。
 所有M是S。
∴有些S是P。

${\displaystyle {\cfrac {\cfrac {{\cfrac {\exists x(M(x)\land P(x))}{\exists x(P(x)\land M(x))}}\qquad {\begin{matrix}\quad \\\forall x(M(x)\rightarrow S(x))\end{matrix}}}{\forall x(M(x)\rightarrow S(x))\qquad \exists x(P(x)\land M(x))}}{\cfrac {\exists x(P(x)\land S(x))}{\exists x(S(x)\land P(x))}}}}$

（IAI-3是IAI-4的等价形式。）

• OAO（Bocardo）

 有些M不是P。
 所有M是S。
∴有些S不是P。

${\displaystyle {\cfrac {\cfrac {{\cfrac {\exists x(M(x)\land \lnot P(x))}{\exists x((\lnot P(x))\land M(x))}}\quad {\begin{matrix}\quad \\\forall x(M(x)\rightarrow S(x))\end{matrix}}}{\forall x(M(x)\rightarrow S(x))\quad \exists x((\lnot P(x))\land M(x))}}{\cfrac {\exists x((\lnot P(x))\land S(x))}{\exists x(S(x)\land \lnot P(x))}}}}$

（这种形式还有其他推导方法。）^[6]

增补的论式

第4格由亚里士多德的学生泰奥弗拉斯托斯补充^[7]。

第4格

• AAI（Bamalip）

 所有P是M。
 所有M是S。
∴有些S是P。
（这种形式需要假定有些P确实存在。）

${\displaystyle {\cfrac {{\cfrac {\cfrac {\forall x(P(x)\rightarrow M(x))\qquad \forall x(M(x)\rightarrow S(x))}{\forall x(M(x)\rightarrow S(x))\qquad \forall x(P(x)\rightarrow M(x))}}{\forall x(P(x)\rightarrow S(x))}}\quad {\cfrac {\exists xP(x)}{\exists x(P(x)\land P(x))}}}{\cfrac {\exists x(P(x)\land S(x))}{\exists x(S(x)\land P(x))}}}}$

• EAO（Fesapo）

 没有P是M。
 所有M是S。
∴有些S不是P。

（这种形式需要假定有些M确实存在。）^[8]

${\displaystyle {\cfrac {{\begin{matrix}\quad \\\quad \\{\cfrac {\forall x(P(x)\rightarrow \lnot M(x))}{\forall x(M(x)\rightarrow \lnot P(x))}}\end{matrix}}\,{\cfrac {{\begin{matrix}\quad \\\forall x(M(x)\rightarrow S(x))\end{matrix}}\quad {\cfrac {\exists xM(x)}{\exists x(M(x)\land M(x))}}}{\cfrac {\exists x(M(x)\land S(x))}{\exists x(S(x)\land M(x))}}}}{\exists x(S(x)\land \lnot P(x))}}}$

（EAO-4是EAO-3的等价形式。）

• AEE（Calemes）

 所有P是M。
 没有M是S。
∴没有S是P。

${\displaystyle {\cfrac {\cfrac {\forall x(P(x)\rightarrow M(x))\qquad \forall x(M(x)\rightarrow \lnot S(x))}{\forall x(M(x)\rightarrow \lnot S(x))\qquad \forall x(P(x)\rightarrow M(x))}}{\cfrac {\forall x(P(x)\rightarrow \lnot S(x))}{\forall x(S(x)\rightarrow \lnot P(x))}}}}$

• EIO（Fresison）

 没有P是M。
 有些M是S。
∴有些S不是P。

${\displaystyle {\cfrac {{\cfrac {\forall x(P(x)\rightarrow \lnot M(x))}{\forall x(M(x)\rightarrow \lnot P(x))}}\qquad {\cfrac {\exists x(M(x)\land S(x))}{\exists x(S(x)\land M(x))}}}{\exists x(S(x)\land \lnot P(x))}}}$

（EIO-4是EIO-1的等价形式。）

• IAI（Dimaris）

 有些P是M。
 所有M是S。
∴有些S是P。

${\displaystyle {\cfrac {\cfrac {\exists x(P(x)\land M(x))\qquad \forall x(M(x)\rightarrow \ S(x))}{\forall x(M(x)\rightarrow \ S(x))\qquad \exists x(P(x)\land M(x))}}{\cfrac {\exists x(P(x)\land S(x))}{\exists x(S(x)\land P(x))}}}}$

结论弱化的论式

历史上，AAI-3、EAO-3、AAI-4、EAO-4的拉丁语名字中有字母“p”，用来指示出这些论式通过引入了某个词项确实有元素存在的前提，将一个A命题弱化成了I命题。后人认为它们不是直言的即不是无条件的，这个问题被称为存在性引入问题。

在假定结论的主词确定有成员存在的前提下，可将论式中的结论A弱化为结论I，结论E弱化为结论O，它们也可以被增补为有效论式，从而得到所有可能的24有效论式。结论弱化论式有5个：AAI-1（Barbari），即弱化的AAA-1；EAO-1（Celaront），即弱化的EAE-1；AEO-2（Camestros），即弱化的AEE-2；EAO-2（Cesaro），即弱化的EAE-2；AEO-4（Calemos），即弱化的AEE-4。AAI-1的结论同于AII-1的结论，EAO-1、EAO-2的结论同于EIO-1的结论，AEO-2、AEO-4的结论同于AOO-2的结论，需要注意结论弱化论式原来的结论依然成立。

谓词演算公式的注解

按照布尔逻辑和集合代数的观点，三段论可以解释为：集合（类）${\displaystyle \,S\,}$和集合${\displaystyle \,M\,}$有某种二元关系，并且集合${\displaystyle \,M\,}$和集合${\displaystyle \,P\,}$有某种二元关系，从而推论出集合${\displaystyle \,S\,}$和集合${\displaystyle \,P\,}$是否存在进而为何种可确定的二元关系。两个集合之间的二元关系用直言命题可确定的有四种：

• A（全称肯定）命题：所有${\displaystyle \,M\,}$的元素是${\displaystyle \,N\,}$的元素，确定了${\displaystyle \,M\,}$“包含于”${\displaystyle \,N\,}$的关系，${\displaystyle \,M\,}$是${\displaystyle \,N\,}$的子集，${\displaystyle \,N\,}$是${\displaystyle \,M\,}$的超集，这是一种偏序关系，${\displaystyle \,L\,}$包含于${\displaystyle \,M\,}$，并且${\displaystyle \,M\,}$包含于${\displaystyle \,N\,}$，则${\displaystyle \,L\,}$包含于${\displaystyle \,N\,}$。A命题允许两个推理方向，从元素属于${\displaystyle \,M\,}$推出它属于${\displaystyle \,N\,}$，从元素不属于${\displaystyle \,N\,}$推出它不属于${\displaystyle \,M\,}$。A命题确定了${\displaystyle \,M\,}$减${\displaystyle \,N\,}$的差集是空集。
• E（全称否定）命题：所有${\displaystyle \,M\,}$的元素不是${\displaystyle \,N\,}$的元素，确定了${\displaystyle \,M\,}$和${\displaystyle \,N\,}$是“无交集”的关系，这是一种对称关系，${\displaystyle \,M\,}$无交集于${\displaystyle \,N\,}$，同于${\displaystyle \,N\,}$无交集于${\displaystyle \,M\,}$。E命题允许两个推理方向，从元素属于${\displaystyle \,M\,}$推出它不属于${\displaystyle \,N\,}$，从元素属于${\displaystyle \,N\,}$推出它不属于${\displaystyle \,M\,}$。E命题确定了${\displaystyle \,M\,}$与${\displaystyle \,N\,}$的交集是空集。
• I（特称肯定）命题：有些${\displaystyle \,M\,}$的元素是${\displaystyle \,N\,}$的元素，确定了${\displaystyle \,M\,}$和${\displaystyle \,N\,}$是“有交集”的关系，这是一种对称关系，${\displaystyle \,M\,}$有交集于${\displaystyle \,N\,}$，同于${\displaystyle \,N\,}$有交集于${\displaystyle \,M\,}$。I命题确定了${\displaystyle \,M\,}$与${\displaystyle \,N\,}$的交集不是空集。
• O（特称否定）命题：有些${\displaystyle \,M\,}$的元素不是${\displaystyle \,N\,}$的元素，确定了${\displaystyle \,M\,}$“不包含于”${\displaystyle \,N\,}$的关系。O命题确定了${\displaystyle \,M\,}$减${\displaystyle \,N\,}$的差集不是空集。

两个全称命题可以推出一个新的全称命题，一个全称命题和一个特称命题可以推出一个新的特称命题，两个特称命题无法推理。A命题可以和所有四种命题组合。E命题还可以和I命题组合，两个否定命题和IE组合，不能得出属于四种命题之一的结论。故而有效的论式，要在AA、AE、EA、AI、IA、AO、OA、EI这8种组合乘以4种格，共32种情况中找出。

AA组合中AAA-1是直接推出的；第4格AA组合推论出谓词包含于主词的关系，这不是四种命题之一，只能在谓词确实有元素存在的前提下弱化为AAI-4。AE组合中AEE-4是直接推出的，EA组合中EAE-1是直接推出的。第3格AA组合和EA组合，在中项确定有元素存在的前提下，形成AAI-3和EAO-3。AAA-1、AAI-4、AAI-3没有等价者。通过对换其前提E命题中主词和谓词的位置，从AEE-4得出其等价者AEE-2，从EAE-1的得出其等价者EAE-2，从EAO-3得出其等价者EAO-4。

AII-1、IAI-4是直接推出的，通过对换其前提I命题中主词和谓词的位置，从AII-1得出其等价者AII-3，从IAI-4得出其等价者IAI-3。AOO-2和OAO-3在历史上采用了反证法，这里采用了直接推理中的“对置法”，AOO-2、OAO-3没有等价者。EIO-1是直接推出的，通过对换其前提E命题及/或（英语：And/or）I命题中主词和谓词的位置，从EIO-1得出其等价者EIO-2、EIO-3、EIO-4。

24论式图示

下表以文氏图展示24个有效直言三段论，不同栏表示不同的前提，不同外框颜色表示不同的结论，需要存在性预设的推理以虚线与斜体字标示。

格	A ∧ A		A ∧ E				A ∧ I		A ∧ O		E ∧ I
	AAA	AAI	AEE	AEO	EAE	EAO	AII	IAI	AOO	OAO	EIO
1	Barbara	Barbari			Celarent	Celaront	Darii				Ferio
2			Camestres	Camestros	Cesare	Cesaro			Baroco		Festino
3		Darapti				Felapton	Datisi	Disamis		Bocardo	Ferison
4		Bamalip	Calemes	Calemos		Fesapo		Dimatis			Fresison

参见

• 直接推理
• 传统逻辑
• 谓词演算

注解

1. 中国社会科学院语言研究所词典编辑室. 现代汉语词典 2016年9月第七版. 商务印书馆. 2016: 1121-1122 [2020-07-05]. ISBN 978-7-100-12450-8 （中文（大陆简体））. .......【三段论】.......由大前提和小前提推出结论。如“凡金属都能导电”（大前提），“铜是金属”（小前提），“所以铜能导电”（结论）。....... 引文格式1维护：未识别语文类型 (link)
2. 这个论式还可以推导为：
   ${\displaystyle {\cfrac {{\cfrac {\cfrac {\forall x(P(x)\rightarrow M(x))}{\forall x(P(x)\rightarrow \lnot (\lnot M(x)))}}{\forall x((\lnot M(x))\rightarrow \lnot P(x))}}\quad {\cfrac {\forall x(S(x)\rightarrow \lnot M(x))}{\forall x(S(x)\rightarrow (\lnot M(x)))}}}{\forall x(S(x)\rightarrow \lnot P(x))}}}$
3. 这个论式还可以采用反证法来推导：
   ${\displaystyle {\begin{aligned}&{\cfrac {{\cfrac {{\begin{matrix}\quad \\\forall x(P(x)\rightarrow M(x))\end{matrix}}\quad {\cfrac {\lnot (\exists x(S(x)\land \lnot P(x)))}{\forall x(S(x)\rightarrow P(x))}}}{\forall x(S(x)\rightarrow M(x))}}\quad {\cfrac {\exists x(S(x)\land \lnot M(x))}{\exists x((\lnot M(x))\land S(x))}}}{\cfrac {\exists x((\lnot M(x))\land M(x))}{\bot }}}\\\implies &{\cfrac {\forall x(P(x)\rightarrow M(x))\qquad \exists x(S(x)\land \lnot M(x))}{\exists x(S(x)\land \lnot P(x))}}\end{aligned}}}$
4. 直接结论是：所有M是P且S。
   ${\displaystyle {\cfrac {{\cfrac {\cfrac {\forall x(M(x)\rightarrow P(x))\qquad \forall x(M(x)\rightarrow S(x))}{\forall x(M(x)\rightarrow (P(x)\land S(x)))}}{\forall x(M(x)\rightarrow (S(x)\land P(x)))}}\qquad {\begin{matrix}\quad \\\exists xM(x)\end{matrix}}}{\exists x(S(x)\land P(x))}}}$
5. 直接结论是：所有M是S且非P。
   ${\displaystyle {\cfrac {{\cfrac {\cfrac {\forall x(M(x)\rightarrow \lnot P(x))\qquad \forall x(M(x)\rightarrow S(x))}{\forall x(M(x)\rightarrow ((\lnot P(x))\land S(x)))}}{\forall x(M(x)\rightarrow (S(x)\land \lnot P(x)))}}\quad {\begin{matrix}\quad \\\exists xM(x)\end{matrix}}}{\exists x(S(x)\land \lnot P(x))}}}$
6. 这个论式还可以采用反证法来推导：
   ${\displaystyle {\begin{aligned}&{\cfrac {{\cfrac {{\cfrac {\lnot (\exists x(S(x)\land \lnot P(x)))}{\forall x(S(x)\rightarrow P(x))}}\quad {\begin{matrix}\quad \\\forall x(M(x)\rightarrow S(x))\end{matrix}}}{\forall x(M(x)\rightarrow P(x))}}\quad {\cfrac {\exists x(M(x)\land \lnot P(x))}{\exists x((\lnot P(x))\land M(x))}}}{\cfrac {\exists x((\lnot P(x))\land P(x))}{\bot }}}\\\implies &{\cfrac {\exists x(M(x)\land \lnot P(x))\qquad \forall x(M(x)\rightarrow S(x))}{\exists x(S(x)\land \lnot P(x))}}\end{aligned}}}$
7. 在亚里士多德《前分析篇》里关于AEE-2的论证中，对小前提进行对换主词与谓词位置之后，得出第4格的AEE-4，亚里士多德称之为再次得到了第1格，没有因为大项和小项位置颠倒而专门称之为第4格。在亚里士多德的定义中第1格为中项既是一个前提的主词又是另一个前提的谓词。第4格中有4个论式是其他格的等价形式、1个论式是结论弱化形式，因此亚里士多德三段论体系并无缺失。
8. 直接结论是：所有M是S且非P。
   ${\displaystyle {\cfrac {{\cfrac {\cfrac {{\cfrac {\forall x(P(x)\rightarrow \lnot M(x))}{\forall x(M(x)\rightarrow \lnot P(x))}}\qquad {\begin{matrix}\quad \\\forall x(M(x)\rightarrow S(x))\end{matrix}}}{\forall x(M(x)\rightarrow ((\lnot P(x))\land S(x)))}}{\forall x(M(x)\rightarrow (S(x)\land \lnot P(x)))}}\quad {\begin{matrix}\quad \\\exists xM(x)\end{matrix}}}{\exists x(S(x)\land \lnot P(x))}}}$

引用

• Aristotle, Prior Analytics. transl. Robin Smith（Hackett, 1989）ISBN 0-87220-064-7.
• Blackburn, Simon, 1996. "Syllogism" in the Oxford Dictionary of Philosophy. Oxford University Press. ISBN 0-19-283134-8.
• Broadie, Alexander, 1993. Introduction to Medieval Logic. Oxford University Press. ISBN 0-19-824026-0.
• Irving Copi, 1969. Introduction to Logic, 3rd ed. Macmillan Company.
• Hamblin, Charles L., 1970. Fallacies, Methuen : London, ISBN 0-416-70070-5. Cf. on validity of syllogisms: "A simple set of rules of validity was finally produced in the later Middle Ages, based on the concept of Distribution.“
• Jan Łukasiewicz, 1987 (1957). Aristotle's Syllogistic from the Standpoint of Modern Formal Logic. New York: Garland Publishers. ISBN 0824069242. OCLC 15015545.

外部链接

• Robin Smith. Aristotle's Logic. 扎尔塔, 爱德华·N (编). 《斯坦福哲学百科全书》.
• Terence Parsons. The Traditional Square of Opposition. 扎尔塔, 爱德华·N (编). 《斯坦福哲学百科全书》.
• Henrik Lagerlund. Medieval Theories of the Syllogism. 扎尔塔, 爱德华·N (编). 《斯坦福哲学百科全书》.
• Aristotle's Prior Analytics: the Theory of Categorical Syllogism （页面存档备份，存于互联网档案馆） an annotated bibliography on Aristotle's syllogistic
• Abbreviatio Montana （页面存档备份，存于互联网档案馆） article by Prof. R. J. Kilcullen of Macquarie University on the medieval classification of syllogisms.
• The Figures of the Syllogism （页面存档备份，存于互联网档案馆） is a brief table listing the forms of the syllogism.
• www.fibonicci.co.uk/syllogisms some fun syllogism tests/quizzes
• Syllogistic Reasoning in Buddhism - Example & Worksheet

传统逻辑：三段论

形式：直言三段论 | 选言三段论 | 假言三段论 | 复合三段论 | 准三段论 | 统计三段论

其他：对立四边形 | 布尔三段论 | 三段论谬论