根轨迹图

根轨迹图（root locus）是控制理论及稳定性理论中，作图分析的方式，可以看到在特定参数（一般会是反馈系统的环路增益）变化时，系统极点的变化。根轨迹图是由Walter R. Evans（英语：Walter R. Evans）所发展的技巧，是经典控制理论中的稳定性判据，可以判断线性时不变系统是否稳定。

一个根轨迹图，部分的极点在右半平面，表示当时的系统会不稳定

根轨迹图是在复数s-平面中，系统闭环传递函数的极点随着增益参数的变化（引用极零点图（英语：Pole–zero plot））。

用途

极点位置及二阶系统中自然频率及阻尼比的关系

除了确认系统的稳定性外，根轨迹图也可以用来设计反馈系统的阻尼比（ζ）及自然频率（ω_n）。定阻尼比的线是从原点往外延伸的线，而固定自然频率的线是圆心在原点的圆弧。在根轨迹图上选择有想要的阻尼比及自然频率的点，可以计算增益K并且实现其控制器。在许多教材科书上有利用根轨迹图设计控制器的精细技巧，例如超前-滞后补偿器、PI、PD及PID控制器都可以用此技巧来近似设计。

以上使用阻尼比及自然频率的定义，前提是假设整个反馈系统可以用二阶系统来近似，也就是说系统有一对主要的复数极点，不过多半的情形都不是如此，因此在实做时仍需要针对系统再进行模拟，确认符合需求。

定义

反馈系统的根轨迹图是用作图的方式在复数s-平面上画出在系统参数变化时，反馈系统闭环极点的可能位置。这些点是根轨迹图中满足角度条件（angle condition）的点。根轨迹图中特定点的参数数值可以用量值条件（magnitude condition）来计算。

假设有个反馈系统，输入信号${\displaystyle X(s)}$、输出信号${\displaystyle Y(s)}$。其顺向路径传递函数为${\displaystyle G(s)}$，反馈路径传递函数为${\displaystyle H(s)}$。

此系统的闭环传递函数为^[1]

${\displaystyle T(s)={\frac {Y(s)}{X(s)}}={\frac {G(s)}{1+G(s)H(s)}}}$

因此，闭环传递函数的极点为特征方程式${\displaystyle 1+G(s)H(s)=0}$的根，方程式的根可以令${\displaystyle G(s)H(s)=-1}$来求得。

若是一个没有纯粹延迟的系统，${\displaystyle G(s)H(s)}$的乘积为有理的多项式函数，可以表示为^[2]

${\displaystyle G(s)H(s)=K{\frac {(s+z_{1})(s+z_{2})\cdots (s+z_{m})}{(s+p_{1})(s+p_{2})\cdots (s+p_{n})}}}$

其中${\displaystyle -z_{i}}$为${\displaystyle m}$个零点，${\displaystyle -p_{i}}$为${\displaystyle n}$个极点，而${\displaystyle K}$为增益。一般而言，root locus diagram会标示在不同参数${\displaystyle K}$时，传递函数极点的位置。而root locus plot就会画出针对任意${\displaystyle K}$值下，使${\displaystyle G(s)H(s)=-1}$的极点 ，但无法看出${\displaystyle K}$值变化时，极点移动的趋势。

因为只有${\displaystyle K}$的系数以及简单的单项，此有理多项式的值可以用向量的技巧来计算，也就是将量值相乘或是相除，角度相加或是相减。向量公式的由来是因为有理多项式${\displaystyle G(s)H(s)}$的每一个因式${\displaystyle (s-a)}$就表示一个s-平面下由${\displaystyle a}$到${\displaystyle s}$的向量，因此可以透过计算每一个向量的量值及角度来计算多项式。

根据矩阵数学，有理多项式的相角等于所有分子项的角度和，减去所有分母项的角度和。因此若要测试s-平面上的一点是否在根轨迹图上，只要看开环的零点及极点即可，这称为角度条件。

有理多项式的量值也是所有分子项的量值乘积，再除以所有分母项量值的乘积。若只是要确认一个s-平面上的点是否在根轨迹图上，不需要计算有理多项式的量值，因为${\displaystyle K}$值会变，而且可以是任意的整数。针对根轨迹图上的每一点，都可以计算其对应的${\displaystyle K}$值，此即为量值条件。

以前绘制根轨迹图会使用名叫Spirule的特殊量角器，可以用来确认角度并且绘制根轨迹图^[3]

根轨迹图只能提供在增益${\displaystyle K}$变化时闭环极点的位置信息。${\displaystyle K}$的数值不影响零点的位置，闭环零点和开环的零点相同。

角度条件

主条目：角度条件

复数s平面上的点${\displaystyle s}$若满足下式，即符合角度条件（angle condition）

${\displaystyle \angle (G(s)H(s))=\pi +2k\pi }$

其中${\displaystyle k}$为整数。

也就是说

${\displaystyle \sum _{i=1}^{m}\angle (s+z_{i})-\sum _{i=1}^{n}\angle (s+p_{i})=\pi +2k\pi }$

开环零点到${\displaystyle s}$点角度的和，减去开环极点到${\displaystyle s}$点角度的和，除${\displaystyle 2\pi }$后的余数需等于${\displaystyle \pi }$。

量值条件

主条目：量值条件

在根轨迹图上的特定点${\displaystyle s}$，数值${\displaystyle K}$若使下式成立，就符合量值条件（magnitude condition）

${\displaystyle |G(s)H(s)|=1}$

也就是说

${\displaystyle K{\frac {|s+z_{1}||s+z_{2}|\cdots |s+z_{m}|}{|s+p_{1}||s+p_{2}|\cdots |s+p_{n}|}}=1}$.

绘制根轨迹图

RL=根轨迹图，ZARL=zero angle root locus

利用一些基本的技巧，可以用根轨迹法绘制Ｋ值变化时极点的轨迹。根轨迹图可以看出反馈系统在不同 ${\displaystyle K}$ 下的稳定性以及动态特性^[4][5]。其规则如下：

• 标示开环的极点及零点
• 将实轴上，在奇数个极点及零点左边的线段标示下来（例如一个、三个极点及零点）。
• 找渐近线

令P为极点的个数，Z为零点的个数，两者相减即为渐近线的数量：

${\displaystyle P-Z={\text{number of asymptotes}}\,}$

渐近线和实轴的交点在${\displaystyle \alpha }$（称为形心），往外延伸的角度为${\displaystyle \phi }$：

${\displaystyle \phi _{l}={\frac {180^{\circ }+(l-1)360^{\circ }}{P-Z}},l=1,2,\ldots ,P-Z}$

${\displaystyle \alpha ={\frac {\sum _{P}-\sum _{Z}}{P-Z}}}$

其中${\displaystyle \sum _{P}}$为所有极点数值的和，${\displaystyle \sum _{Z}}$为所有明确零点数值的和

• 根据测试点的相位条件判断其往外延伸的角度
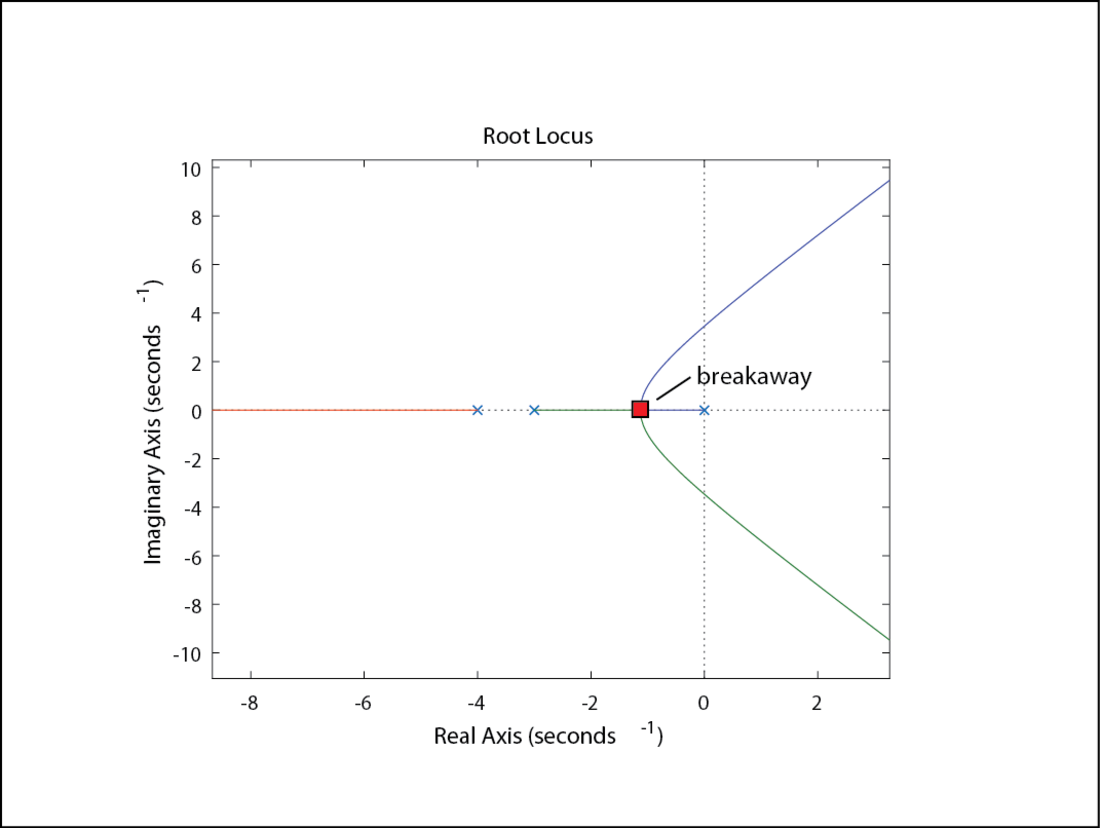
• 计算分离点（breakaway/break-in points）

根轨迹图上的分离点（二条根轨迹图上的轨迹相交的点）是满足下式的根

${\displaystyle {\frac {dG(s)H(s)}{ds}}=0{\text{ or }}{\frac {d{\overline {GH}}(z)}{dz}}=0}$

只要解开z，实根即为分离点，若是虚数，表示没有分离点。

相关条目

• 劳斯–赫尔维茨稳定性判据
• 奈奎斯特稳定判据
• 增益裕度及相位裕度
• 波特图
• 相位裕度

参考资料

1. Kuo 1967，第331页.
2. Kuo 1967，第332页.
3. Evans, Walter R., Spirule Instructions, Whittier, CA: The Spirule Company, 1965
4. Evans, W. R., Graphical Analysis of Control Systems, Trans. AIEE, January 1948, 67 (1): 547–551, ISSN 0096-3860, doi:10.1109/T-AIEE.1948.5059708
5. Evans, W. R., Control Systems Synthesis by Root Locus Method, Trans. AIEE, January 1950, 69 (1): 66–69, ISSN 0096-3860, doi:10.1109/T-AIEE.1950.5060121

• Kuo, Benjamin C., Root Locus Technique, Automatic Control Systems second, Englewood Cliffs, NJ: Prentice-Hall: 329–388, 1967, ASIN B000KPT04C, LCCN 67016388, OCLC 3805225

延伸阅读

• Ash, R. H.; Ash, G. H., Numerical Computation of Root Loci Using the Newton-Raphson Technique, IEEE Trans. Automatic Control, October 1968, 13 (5), doi:10.1109/TAC.1968.1098980
• Williamson, S. E., Design Data to assist the Plotting of Root Loci (Part I), Control Magazine, May 1968, 12 (119): 404–407
• Williamson, S. E., Design Data to assist the Plotting of Root Loci (Part II), Control Magazine, June 1968, 12 (120): 556–559
• Williamson, S. E., Design Data to assist the Plotting of Root Loci (Part III), Control Magazine, July 1968, 12 (121): 645–647
• Williamson, S. E., Computer Program to Obtain the Time Response of Sampled Data Systems, IEE Electronics Letters, May 15, 1969, 5 (10): 209–210, doi:10.1049/el:19690159
• Williamson, S. E., Accurate Root Locus Plotting Including the Effects of Pure Time Delay (PDF), Proc. IEE, July 1969, 116 (7): 1269–1271, doi:10.1049/piee.1969.0235

外部链接

• Wikibooks: Control Systems/Root Locus
• Carnegie Mellon / University of Michigan Tutorial
• Excellent examples. Start with example 5 and proceed backwards through 4 to 1. Also visit the main page
• The root-locus method: Drawing by hand techniques
• "RootLocs": A free multi-featured root-locus plotter for Mac and Windows platforms
• "Root Locus": A free root-locus plotter/analyzer for Windows
• Root Locus at ControlTheoryPro.com
• Root Locus Analysis of Control Systems
• MATLAB function for computing root locus of a SISO open-loop model
• Wechsler, E. R., Root Locus Algorithms for Programmable Pocket Calculators (PDF), NASA: 60–64, January–March 1983 [2017-06-02], TDA Progress Report 42-73, （原始内容 (PDF)存档于2016-12-24）
• Mathematica function for plotting the root locus （页面存档备份，存于互联网档案馆）