在数学中,如果在某个集合 上定义的具有实数或复数值的某个函数
上定义的具有实数或复数值的某个函数 的值域是有界集合,则函数
的值域是有界集合,则函数 被称为有界的(或有界函数)。换句话说,存在实数
被称为有界的(或有界函数)。换句话说,存在实数 ,使得对于集合
,使得对于集合 中的所有
中的所有 ,都有
,都有 。有时,如果对于集合
。有时,如果对于集合 中的所有
中的所有 ,都有
,都有 ,则函数
,则函数 称为上有界的,
称为上有界的, 就是它的一个上界;如果对于集合
就是它的一个上界;如果对于集合 中的所有
中的所有 ,都有
,都有 ,则函数称为下有界的,
,则函数称为下有界的, 就是它的一个下界。
就是它的一个下界。
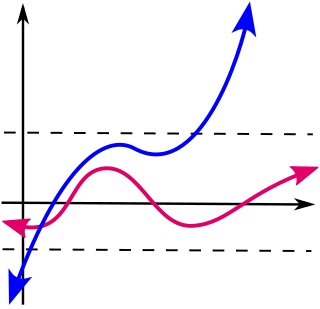 有界函数(红色)和无界函数(蓝色)的示意图。可以看到,有界函数的图形保持在(虚线)水平带内,而无界函数的图形不保持在水平带内。
有界函数(红色)和无界函数(蓝色)的示意图。可以看到,有界函数的图形保持在(虚线)水平带内,而无界函数的图形不保持在水平带内。
一个特例是有界数列,其中 是所有自然数所组成的集合
是所有自然数所组成的集合 。所以,一个数列
。所以,一个数列 是有界的,如果存在一个数
是有界的,如果存在一个数 ,使得对于所有的自然数
,使得对于所有的自然数 ,都有
,都有 。
。




















![{\displaystyle f:[0,1]\rightarrow R}](http://wikimedia.org/api/rest_v1/media/math/render/svg/f07e139ee2aaa7c0d9233199f0c6ca7876b65bd6)