二进分数

二进分数，也称为二进有理数，是一种分母是2的幂的分数。可以表示成${\displaystyle {\frac {a}{2^{b}}}}$，其中，${\displaystyle a}$是一个整数，${\displaystyle b}$是一个自然数。例如：${\displaystyle {\frac {1}{2}}}$，${\displaystyle {\frac {3}{8}}}$，而${\displaystyle {\frac {1}{3}}}$就不是。(英制单位中广泛采用二进分数，例如${\displaystyle {\frac {3}{4}}}$英寸，${\displaystyle {\frac {1}{16}}}$英寸，${\displaystyle {\frac {1}{2}}}$磅。)

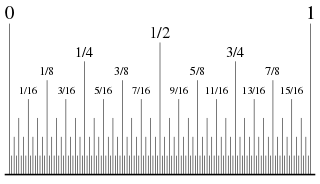从0到1的二进分数。

各种各样的数

基本

${\displaystyle \mathbb {N} \subseteq \mathbb {Z} \subseteq \mathbb {Q} \subseteq \mathbb {R} \subseteq \mathbb {C} }$ 正数 ${\displaystyle \mathbb {R} ^{+}}$ 自然数 ${\displaystyle \mathbb {N} }$ 正整数 ${\displaystyle \mathbb {Z} ^{+}}$ 小数 有限小数 无限小数 循环小数 有理数 ${\displaystyle \mathbb {Q} }$ 代数数 ${\displaystyle \mathbb {A} }$ 实数 ${\displaystyle \mathbb {R} }$ 复数 ${\displaystyle \mathbb {C} }$ 高斯整数 ${\displaystyle \mathbb {Z} [i]}$ 负数 ${\displaystyle \mathbb {R} ^{-}}$ 整数 ${\displaystyle \mathbb {Z} }$ 负整数 ${\displaystyle \mathbb {Z} ^{-}}$ 分数 单位分数 二进分数 规矩数 无理数 超越数 虚数 ${\displaystyle \mathbb {I} }$ 二次无理数 艾森斯坦整数 ${\displaystyle \mathbb {Z} [\omega ]}$

延伸

二元数 四元数 ${\displaystyle \mathbb {H} }$ 八元数 ${\displaystyle \mathbb {O} }$ 十六元数 ${\displaystyle \mathbb {S} }$ 超实数 ${\displaystyle ^{*}\mathbb {R} }$ 大实数 上超实数 双曲复数 双复数 复四元数 共四元数（英语：Dual quaternion） 超复数 超数 超现实数

其他

质数 ${\displaystyle \mathbb {P} }$ 可计算数 基数 阿列夫数 同余 整数数列 公称值 规矩数 可定义数 序数 超限数 p进数 数学常数 圆周率 ${\displaystyle \pi =3.14159265}$… 自然对数的底 ${\displaystyle e=2.718281828}$… 虚数单位 ${\displaystyle i={\sqrt {-{1}}}}$ 无限大 ${\displaystyle \infty }$

查 论 编

所有二进分数组成的集合在实数轴上是稠密的：任何实数${\displaystyle x}$都可以用形为${\displaystyle \lfloor 2^{i}x\rfloor /2^{i}}$的二进分数无限逼近。与实数轴上的其它稠密集，例如有理数相比，二进分数是相对“小”的稠密集，这就是为什么它们有时出现在证明中（例如乌雷松引理）。

任何两个二进分数的和、积，与差也是二进分数：

${\displaystyle {\frac {a}{2^{b}}}+{\frac {c}{2^{d}}}={\frac {2^{d-b}a+c}{2^{d}}}\quad (d\geq b)}$

${\displaystyle {\frac {a}{2^{b}}}-{\frac {c}{2^{d}}}={\frac {2^{d-b}a-c}{2^{d}}}\quad (d\geq b)}$

${\displaystyle {\frac {a}{2^{b}}}-{\frac {c}{2^{d}}}={\frac {a-2^{b-d}c}{2^{b}}}\quad (d<b)}$

${\displaystyle {\frac {a}{2^{b}}}\times {\frac {c}{2^{d}}}={\frac {a\times c}{2^{b+d}}}.}$

但是，两个二进分数的商则一般不是二进分数。因此，二进分数形成了有理数${\displaystyle \mathbb {Q} }$的一个子环。