热门问题
时间线
聊天
视角
反正割
来自维基百科,自由的百科全书
Remove ads
反正割(英语:arcsecant[3]、记为:或)是一种反三角函数[4],对应的三角函数为正割函数,用来计算已知斜边与邻边的比值求出其夹角大小的函数,是高等数学中的一种基本特殊函数,其输入值与反余弦互为倒数。
 | |
| 性质 | |
| 奇偶性 | 非奇非偶 |
| 定义域 | [1] |
| 到达域 | |
| 周期 | N/A |
| 特定值 | |
| 当x=0 | 不存在[注 1] |
| 当x=+∞ | (90°) |
| 当x=-∞ | (90°) |
| 当x=1 | 0 |
| 当x=-1 | (180°) |
| 其他性质 | |
| 渐近线 | (y=90°) |
由于正割函数在实数上不具有一一对应的关系,所以不存在反函数,但我们可以限制其定义域,因此,反正割是单射也是可逆的,由于限制正割函数的定义域在([0, 180°])时,其值域是全体实数,但在区间不存在。
Remove ads
符号
反正割一般记为[5]或[6][7][8][9],以表示正割的反函数。也有以大写书写的版本Arcsec z[10]和Sec−1 z一般用于表示多值函数[6]。在符号上的上标-1是表示反函数,而不是乘法逆元素。但根据ISO 31-11应将反正切函数记为,因为可能会与混淆,是余弦函数。
Remove ads
定义
原始的定义是将正割函数限制在([0, 180°])的反函数
在复变分析中,反正割是这样定义的:
这个动作使反正割被推广到复数。
下图表示推广到复数的反正割复数平面函数图形,可以见到图中央有一条明显的横线正好是实数中未被定义的区间[-1,1]。

Remove ads
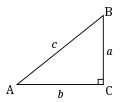
在直角三角形中,反正割定义为已知斜边c与邻边b比值对应的的大小,也就是:
-
直角三角形,C为直角,对于角A而言,a为对边、b为邻边、c为斜边
-
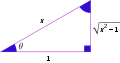
直角三角形,已知斜边斜边为x且邻边为单位长
此外在直角三角形中,若已知斜边为且邻边为单位长,代入反正割可求得对应的角的大小:
因此,根据毕氏定理可以使反正割利用其他反三角函数表示:
Remove ads
若是平面直角坐标系xOy中的一个未知的象限角,是角的终边上一点,是P到原点O的距离,若已知,则可利用反正割求得未知的象限角:
Remove ads
反正割函数可以使用无穷级数定义:
反正割函数的泰勒展开式为:
Remove ads
参见
注释
参考文献
外部链接
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads









![{\displaystyle [0,\pi ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)
![{\displaystyle [-1,1]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
















![{\displaystyle {\begin{aligned}\operatorname {arcsec} z&{}=\arccos \left({\frac {1}{z}}\right)\\&{}={\frac {\pi }{2}}-[z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots ]\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left[{\frac {(2n)!}{2^{2n}(n!)^{2}}}\right]{\frac {z^{-(2n+1)}}{(2n+1)}};\qquad \left|z\right|\geq 1\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/64761e73f4238c32bdd180b393f18cfc458298fa)
