大星形十二面体

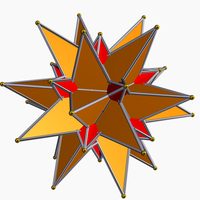
在几何学上，大星形十二面体是一个由五角星组成的非凸正多面体^[1]，是正十二面体的星形多面体，其在非凸均匀多面体被编号为U₅₂、在温尼尔多面体模型被编号为W₂₂。该多面体最早是由温佐·雅姆尼策尔（英语：Wenzel Jamnitzer）于1568年发现并描述^[2][3][4]。后来在1619年时，被约翰尼斯·开普勒重新发现^[5][6][7]。

大星形十二面体

（按这里观看旋转模型）
类别	星形正多面体 星形十二面体
对偶多面体	大二十面体
识别
名称	大星形十二面体
参考索引	U52, C68, W22
鲍尔斯缩写 （verse-and-dimensions的wikia：Bowers acronym）	gissid
数学表示法
考克斯特符号 （英语：Coxeter-Dynkin diagram）
施莱夫利符号	{5/2,3}
威佐夫符号 （英语：Wythoff symbol）	3 | 2 5/2
性质
面	12
边	30
顶点	20
欧拉特征数	F=12, E=30, V=20 （χ=2）
亏格	0
组成与布局
面的种类	12个五角星
面的布局 （英语：Face configuration）	12{5/2}
顶点图	(5/2)3
对称性
对称群	Ih, H3, [5,3], (*532)
特性
正、非凸
图像
(5/2)3 （顶点图） 大二十面体 （对偶多面体）
查 论 编

大星形十二面体的对偶多面体也是一种星形正多面体，同时也是星形二十面体，其为由正三角形构成的大二十面体。

性质

大星形十二面体共有12个面、30条边和20个顶点^[8]，其每个面都是全等的正五角星^[9]、每个顶点都是3个五角星的公共顶点，在顶点图为三角形，可以用(⁵/₂)³来表示^[10]，施莱夫利符号中利用 {⁵/₂,3} 来表示，考克斯特符号（英语：Coxeter-Dynkin digram）中利用来表示。

二面角

大星形十二面体是一种星形正多面体，因此具有所有角相等的性质。其二面角只有一个值，其值为五平方根倒数之反余弦^[11]：

${\displaystyle \cos ^{-1}({\frac {\sqrt {5}}{5}})\approx 1.1071\approx 63.4349^{\circ }}$

顶点坐标

边长为单位长且几何中心位于原点的大星形十二面体，其顶点坐标为^[12]：

${\displaystyle (\pm {\frac {1}{2}},0,\pm {\frac {3-{\sqrt {5}}}{4}})}$、

${\displaystyle (0,\pm {\frac {3-{\sqrt {5}}}{4}},\pm {\frac {1}{2}})}$、

${\displaystyle (\pm {\frac {3-{\sqrt {5}}}{4}},\pm {\frac {1}{2}},0)}$、

${\displaystyle (\pm {\frac {{\sqrt {5}}-1}{4}},\pm {\frac {{\sqrt {5}}-1}{4}},\pm {\frac {{\sqrt {5}}-1}{4}})}$。

作为一个简单多面体

简单多面体是指这个多面体中的面不会与同一个多面体的另一个面相交的多面体。若大星形十二面体要成为一个简单多面体，则需要在这多面体中相交的面上放置新的顶点和边，并将原本的五角星面分割成5个三角形面。这样的多面体共有60个面、90条边和32个顶点^[13]

相关多面体

名称	大星形十二面体	截角大星形十二面体	大截半二十面体	截角大二十面体	大二十面体
考式（英语：Coxeter-Dynkin digram）
图像

对偶复合体

主条目：复合大二十面体大星形十二面体（英语：Compound of great icosahedron and great stellated dodecahedron）

大二十面体与其对偶的复合体为复合大二十面体大星形十二面体。其共有32个面、60条边和32个顶点，其尤拉示性数为4，亏格为-1，有12个非凸面^[14]，是一种截半二十面体的星形多面体^[15][16]。温尼尔在他的书中列出将这种形状编为W₆₁^[17][18]。

从三角形的星状图

从五边形的星状图

参见

• 正十二面体

参考文献

1. Cauchy, A. L. "Recherches sur les polyèdres." J. de l'École Polytechnique 9, 68-86, 1813.

1. Coxeter, Star polytopes and the Schläfli function f(α,β,γ) p. 121 1. The Kepler–Poinsot polyhedra
2. Weisstein, Eric W. (编). 大星形十二面體. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
3. Perspectiva corporum regularium. mathe.tu-freiberg.de. [2017-03-24]. （原始内容存档于2016-10-13）.
4. Geometric Model by A. Harry Wheeler, Great Stellated Dodecahedron. americanhistory.si.edu. [2017-03-24]. （原始内容存档于2017-03-25）.
5. Weisstein, Eric W. (编). Kepler–Poinsot solid. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
6. Johannes Kepler, Harmonices Mundi (1619).
7. Johannes Kepler with E. J. Aiton, A. M. Duncan, and J. V. Field, translators, The Harmony of the World, American Philosophical Society (1997).
8. great stellated dodecahedron. bulatov.org. [2016-09-02]. （原始内容存档于2016-03-26）.
9. Great Stellated Dodecahedron. coolmath. [2016-09-02]. （原始内容存档于2016-08-26）.
10. Cundy, H. and Rollett, A. "Great Stellated Dodecahedron. (⁵/₂)³." §3.6.3 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 94-95, 1989.
11. Kepler-Poinsot Solids: Great Stellated Dodecahedron. dmccooey.com. [2016-09-02]. （原始内容存档于2016-03-24）.
12. Data of Great Stellated Dodecahedron. dmccooey.com. [2016-10-01]. （原始内容存档于2016-10-01）.
13. Alexander Bogomolny. Great Stellated Dodecahedron. cut-the-knot.org. [2016-09-02]. （原始内容存档于2016-08-26）.
14. compound of great stellated dodecahedron and great icosahedron. bulatov.org. [2016-09-02]. （原始内容存档于2015-09-06）.
15. Weisstein, Eric W. (编). Great Icosahedron-Great Stellated Dodecahedron Compound. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
16. H. Cundy and A. Rollett Great Icosahedron Plus Great Stellated Dodecahedron. §3.10.4 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 132-133, 1989.
17. Wenninger, Magnus（英语：Magnus J. Wenninger）. Polyhedron Models. Cambridge University Press. 1974. ISBN 0-521-09859-9.
18. Weisstein, Eric W. (编). Great Icosahedron-Great Stellated Dodecahedron Compound. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.

外部链接

• 埃里克·韦斯坦因. 大星形十二面體. MathWorld.
• Uniform polyhedra and duals