单子 (范畴论)

关于单子在电脑软件的应用，请见“单子 (函数式编程)”。

数学的分支范畴论中，单子（英语：monad），又称三元组（triple, triad）、标准构造（standard construction）、基本构造（fundamental construction）^[1]，是一个内函子（英语：endofunctor）（即由某范畴映到自身的函子），连同满足特定连贯条件（英语：coherence condition）的两个自然变换，三者构成的整体。单子用于研究互为伴随的函子对，并将偏序集上的闭包算子推广到任意范畴。

导论与定义

单子是一类内函子（英语：endofunctor）（连同其他资讯）。例如，若${\displaystyle F}$和${\displaystyle G}$为一对伴随函子，${\displaystyle F}$为${\displaystyle G}$的左伴随，则复合${\displaystyle G\circ F}$是单子。若${\displaystyle F}$与${\displaystyle G}$互为逆函子，则对应的单子是恒等函子。一般而言，伴随关系并不等同范畴的等价，而可以联系不同性质的范畴。为了探讨伴随关系所“保持”的性质，数学家研究单子论。理论的另一半，即藉考虑${\displaystyle F\circ G}$，以研究伴随关系，是单子论的对偶理论。该类函子称为余单子（英语：comonad）。

严格定义

本条目中，${\displaystyle {\mathcal {C}}}$皆表示某范畴。${\displaystyle {\mathcal {C}}}$上的单子是函子${\displaystyle T:{\mathcal {C}}\to {\mathcal {C}}}$，连同两个自然变换，分别是单位${\displaystyle \eta :1_{\mathcal {C}}\to T}$（其中${\displaystyle 1_{\mathcal {C}}}$是${\displaystyle {\mathcal {C}}}$上的恒等函子）与乘法${\displaystyle \mu :T^{2}\to T}$（其中${\displaystyle T^{2}}$是复合${\displaystyle T\circ T}$，亦是${\displaystyle {\mathcal {C}}}$到${\displaystyle {\mathcal {C}}}$的函子），且要满足下列连贯条件（英语：coherence condition）：

• ${\displaystyle \mu \circ T\mu =\mu \circ \mu T}$（左右皆为${\displaystyle T^{3}\to T}$的自然变换）。此处${\displaystyle T\mu }$与${\displaystyle \mu T}$经水平复合而得。
• ${\displaystyle \mu \circ T\eta =\mu \circ \eta T=1_{T}}$（两者皆为${\displaystyle T\to T}$的自然变换）。此处${\displaystyle 1_{T}}$表示由函子${\displaystyle T}$到自身的恒等自然变换。

以上两式，亦可以下列交换图复述：

记号${\displaystyle T\mu }$与${\displaystyle \mu T}$的含义，参见自然变换，又或考虑以下更具体的写法，不用水平复合记号，并将各函子作用在任意物件${\displaystyle X}$上：

定义中，若将${\displaystyle \mu }$当成幺半群的乘法，则第一条公理类似幺半群（英语：monoid (category theory)）的乘法结合律，而第二条公理类似单位元的存在性（由${\displaystyle \eta }$给出）。准确而言，${\displaystyle {\mathcal {C}}}$上的单子，可以等价地定义为${\displaystyle {\mathcal {C}}}$的内函子范畴${\displaystyle \mathbf {End} _{\mathcal {C}}}$中的幺半群（英语：monoid (category theory)）。（该范畴的物件是${\displaystyle C}$上的内函子，而态射是内函子间的自然变换，幺半结构来自内函子的复合运算。）如此，单子不仅在形式上具有与幺半群相似的公理，甚而单子就是幺半群的特例。

幂集单子

幂集单子${\displaystyle {\mathcal {P}}}$是集合范畴${\displaystyle \mathbf {Set} }$上的单子。其定义中，函子${\displaystyle T}$取为幂集运算，即${\displaystyle T(A)}$为集合${\displaystyle A}$的幂集，而对于函数${\displaystyle f:A\to B}$，${\displaystyle T(f)}$将${\displaystyle A}$的子集映至其像集，即${\displaystyle T(f)(A')=f[A']}$。对每个集合${\displaystyle A}$，有函数${\displaystyle \eta _{A}:A\to T(A)}$，对每个元素${\displaystyle a\in A}$映至单元子集${\displaystyle \{a\}}$， 并有函数

${\displaystyle \mu _{A}\colon T(T(A))\to T(A),}$

将${\displaystyle A}$的若干个子集构成的族，映至该些子集的并集。以上是幂集单子的定义。

两个单子的复合，未必为单子。举例，幂集单子${\displaystyle {\mathcal {P}}}$的二次迭代${\displaystyle {\mathcal {P}}\circ {\mathcal {P}}}$，无法配备单子结构。^[2]

余单子

取上节定义的范畴论对偶（英语：Dual (category theory)），便是余单子（或余三元组）的定义。简单复述，范畴${\displaystyle {\mathcal {C}}}$上的余单子，是对偶范畴（英语：opposite category）${\displaystyle C^{\mathrm {op} }}$上的单子。所以，余单子是由${\displaystyle {\mathcal {C}}}$到${\displaystyle {\mathcal {C}}}$的某个函子${\displaystyle U}$，连同余单位与余乘法（英语：counit and comultiplication）两个自然变换，组成的整体，而三者所要满足的公理，是将原定义中所有态射反转方向而得。

单子之于幺半群，如同余单子之于余幺半群。每个集合皆是余幺半群，且仅有唯一一种方式，所以抽象代数中，较少考虑余幺半群。然而，在线性代数中，向量空间范畴（配备张量积）的余幺半群较为重要，以余代数之名为人所知。

历史

单子的概念最早由罗杰·戈德芒（英语：Roger Godement）于1958年提出^[3]，当时称为“标准构造”（英语：standard construction）。实际上，该书用到的是余单子，用作解决某个层余调（英语：Sheaf cohomology）问题。

其后，单子又出现于彼得·胡伯（Peter Huber）对范畴同伦的研究中。该论文包含由任意一对伴随函子得出单子的证明。^[4]

1965年，海因里希·克莱斯利（英语：Heinrich Kleisli）^[5]，及塞缪尔·艾伦伯格、约翰·柯曼·摩尔（英语：John Coleman Moore）二人^[6]分别独立证明反向的结论，即每个单子皆可由某对伴随函子产生。后一篇论文中，将单子称为“三元组”。

1963年，威廉·洛维尔（英语：William Lawvere）提出泛代数的范畴论。1966年，弗雷德·林顿（Fred Linton）将该理论用单子的语言表达。^[7]单子本身来自拓扑方面的考量，事先似乎比洛维尔的理论更难处理，但已成为用范畴论语言阐述泛代数的方法中，较常见的一个。现今常用的英文名称monad是1971年由桑德斯·麦克兰恩在《现职数学家用的范畴（英语：Categories for the Working Mathematician）》引入，以其类似单子论中的同名哲学概念，即某种能生出其他所有事物的实体。

1980年代，欧金尼奥·莫吉（英语：Eugenio Moggi）在理论计算机科学中，利用单子，为计算机程序的若干方面建立模型，包括例外处理、边界情况。^[8]此后，有多种函数式编程语言仔细实作此想法，作为一种基本规律，同样称为单子。2001年，若干数学家注意到，用单子研究程式标志语意的方法，与洛维尔的理论，两者之间有关联。^[9]。此为代数与语义间的联系，是后来活跃的研究课题。

例子

伴随的复合

若有伴随关系

${\displaystyle F:{\mathcal {C}}\rightleftarrows {\mathcal {D}}:G}$

（即${\displaystyle F}$为${\displaystyle G}$的左伴随，下同），则由此有${\displaystyle {\mathcal {C}}}$上的单子。此普遍的构造，取内函子为复合

${\displaystyle T=G\circ F,}$

而单位自然变换来自伴随的单位${\displaystyle \eta :\operatorname {id} _{\mathcal {C}}\to G\circ F}$，乘法自然变换源自伴随的余单位${\displaystyle \varepsilon }$：

${\displaystyle T^{2}=G\circ F\circ G\circ F\xrightarrow {G\circ \varepsilon \circ F} G\circ F=T.}$

反之，给定单子，可以明确找回一对伴随函子，使单子为该对伴随函子的复合。此构造用到下节定义的${\displaystyle T}$代数的艾伦伯格－摩尔范畴${\displaystyle C^{T}}$。^[10]

两重对偶

给定域${\displaystyle k}$，双重对偶单子（英语：double dualisation monad）源自伴随关系

${\displaystyle (-)^{*}:\mathbf {Vect} _{k}\rightleftarrows \mathbf {Vect} _{k}^{\mathrm {op} }:(-)^{*},}$

其中两个函子${\displaystyle (-)^{*}}$皆将${\displaystyle k}$向量空间${\displaystyle V}$映至对偶空间${\displaystyle V^{*}:=\operatorname {Hom} (V,k)}$，所以对应的单子将向量空间${\displaystyle V}$映至双对偶${\displaystyle V^{**}}$。Kock (1970)对此有更广泛的讨论。

偏序集的闭包算子

偏序集${\displaystyle (P,\leq )}$可以视为特殊的范畴，任意两件物件之间有最多一支态射，且${\displaystyle x}$到${\displaystyle y}$有态射当且仅当偏序中${\displaystyle x\leq y}$。于是，偏序集之间的函子，即是保序映射，而伴随函子对，则组成两偏序集间的伽罗瓦连接，相应的单子是伽罗华连接的闭包算子。

自由遗忘伴随

又举例，设${\displaystyle G}$为群范畴${\displaystyle \mathbf {Grp} }$至集合范畴${\displaystyle \mathbf {Set} }$的遗忘函子，将群映至其基集，又设${\displaystyle F}$为自由函子，由${\displaystyle \mathbf {Set} }$到${\displaystyle \mathbf {Grp} }$，则${\displaystyle F}$是${\displaystyle G}$的左伴随。此时，对应的单子${\displaystyle T=G\circ F}$的作用是，输入一个集合${\displaystyle X}$，输出自由群${\displaystyle F(X)}$的基集，即字母取自${\displaystyle \{x,x^{-1}:x\in X\}}$，且无相邻两个字母互为逆元的字串的集合。

该单子的单位变换，由包含映射

${\displaystyle \eta _{X}:X\rightarrow T(X)}$

给出，该包含映射将${\displaystyle X}$的任意元素，看成仅得一个字元的字串，从而是${\displaystyle T(X)}$的元素。最后，单子的乘法

${\displaystyle \mu _{X}:T(T(X))\rightarrow T(X)}$

是串接或“压平”运算，将若干条字串组成的串，映至该串中所有字串前后连接而成的一条字串。至此描述完单子的两个自然变换。

前述例子中，自由群可以推广至其他种类的代数结构，即泛代数意义下的任意一簇（英语：Variety (universal algebra)）代数。如此，每类代数定义了集合范畴上的一个单子。更重要的是，该类代数的范畴，可从单子找回，即单子的艾伦伯格－摩尔代数范畴，故单子可视为泛代数之簇的推广。

另外，尚有一个单子源自伴随关系。在向量空间范畴${\displaystyle \mathbf {Vect} }$上，若${\displaystyle T}$表示将向量空间${\displaystyle V}$映至其张量代数${\displaystyle T(V)}$的内函子，则相应有单位自然变换将${\displaystyle V}$嵌入到其张量代数，并有乘法自然变换，在${\displaystyle V}$处的分量是态射${\displaystyle T(T(V))\to T(V)}$，将张量积之张量积展开化简。

余密度单子

只要满足某些不强的条件，无左伴随的函子也可以产生单子，称为余密度单子（英语：codensity monad）。例如，从有限集合范畴${\displaystyle \mathbf {FinSet} }$到集合范畴${\displaystyle \mathbf {Set} }$的包含函子无法配备左伴随，但其余密度单子定义在${\displaystyle \mathbf {Set} }$上，将任意集合${\displaystyle X}$映至其上所有超滤子的集合${\displaystyle \beta X}$。 类似例子见于Leinster (2013)。

单子的代数

参见：F代数（英语：F-algebra）和伪代数（英语：pseudoalgebra）

给定范畴${\displaystyle {\mathcal {C}}}$上的单子${\displaystyle (T,\eta ,\mu )}$，可以考虑${\displaystyle {\mathcal {C}}}$中的${\displaystyle {\boldsymbol {T}}}$代数物件。${\displaystyle T}$在该些物件上的作用，与单子的单位与乘法相容。具体而言，${\displaystyle {\boldsymbol {T}}}$代数${\displaystyle (x,h)}$是${\displaystyle {\mathcal {C}}}$中的物件${\displaystyle x}$，连同态射${\displaystyle h:Tx\to x}$（称为该代数的结构映射），使得图

及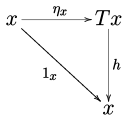

皆可交换。

${\displaystyle T}$代数间的态射${\displaystyle f:(x,h)\to (x',h')}$是${\displaystyle {\mathcal {C}}}$中的态射${\displaystyle f:x\to x'}$，且要使

可交换。于是，${\displaystyle T}$代数及之间的态射组成范畴，称为艾伦伯格－摩尔范畴（英语：Eilenberg–Moore category），记为${\displaystyle {\mathcal {C}}^{T}}$.

例子

自由群单子上的代数

若${\displaystyle T}$为前述自由群单子，则${\displaystyle T}$代数是集合${\displaystyle X}$，连同由${\displaystyle X}$生成的自由群${\displaystyle F(X)}$到${\displaystyle X}$的映射（求值，evaluation），且该映射要满足结合律与单位元的公理。换言之，${\displaystyle X}$本身就具有群结构，而${\displaystyle F(X)}$至${\displaystyle X}$的映射，是将字串按${\displaystyle X}$的群乘法，计算所得的结果

分布单子上的代数

另一个例子是集合范畴上的分布单子（英语：distribution monad）${\displaystyle {\mathcal {D}}}$，其将集合${\displaystyle X}$映至其上所有有限支撑的概率分布的集合。该等分布，是函数${\displaystyle f:X\to [0,1]}$，仅于有限多个元素${\displaystyle x\in X}$处取值非零，而各元素处取值之和为${\displaystyle 1}$。以符号表示，

${\displaystyle {\mathcal {D}}(X)=\left\{f:X\to [0,1]:{\begin{matrix}\#{\text{supp}}(f)<+\infty ,\\\sum _{x\in X}f(x)=1\end{matrix}}\right\}.}$

可由定义证明，分布单子上的代数，等同于凸集，即集合要配备二元运算${\displaystyle +_{r}}$（对每个${\displaystyle r\in [0,1]}$），满足的公理比照欧氏空间中，凸组合${\displaystyle (x,y)\mapsto rx+(1-r)y}$具备的性质。^[11][12]

对称单子上的代数

另一个有用的单子，是交换环${\displaystyle R}$的模范畴${\displaystyle \mathbf {Mod} _{R}}$上的对称代数单子

${\displaystyle {\text{Sym}}^{\bullet }(-):\mathbf {Mod} _{R}\to \mathbf {Mod} _{R}}$

将${\displaystyle R}$模${\displaystyle M}$映到各阶对称张量（英语：symmetric tensor）幂的直和

${\displaystyle {\text{Sym}}^{\bullet }(M)=\bigoplus _{k=0}^{\infty }{\text{Sym}}^{k}(M)}$

其中${\displaystyle {\text{Sym}}^{0}(M)=R}$。例如，${\displaystyle {\text{Sym}}^{\bullet }(R^{\oplus n})\cong R[x_{1},\ldots ,x_{n}]}$，左右两边作为${\displaystyle R}$模同构。如此，对称代数单子上的代数，是交换${\displaystyle R}$代数。类似地，也有反对称张量（英语：Antisymmetric tensor）单子${\displaystyle {\text{Alt}}^{\bullet }(-)}$与全张量单子${\displaystyle T^{\bullet }(-)}$，相应的代数分别是反对称${\displaystyle R}$代数与自由${\displaystyle R}$代数，故

${\displaystyle {\begin{aligned}{\text{Alt}}^{\bullet }(R^{\oplus n})&=R(x_{1},\ldots ,x_{n}),\\{\text{T}}^{\bullet }(R^{\oplus n})&=R\langle x_{1},\ldots ,x_{n}\rangle ,\end{aligned}}}$

前者是${\displaystyle R}$上添加${\displaystyle n}$个生成元的自由反对称代数，而后者则是${\displaystyle n}$个生成元的自由代数。

E∞环谱中的交换代数

对于可交换${\displaystyle \mathbb {S} }$代数（英语：Highly structured ring spectrum），亦有类似的构造，^[13]:113对于可交换${\displaystyle \mathbb {S} }$代数${\displaystyle A}$，对应单子上的代数是可交换的${\displaystyle A}$代数。若${\displaystyle \mathbf {Mod} _{A}}$表示${\displaystyle A}$模的范畴，则可以考虑函子${\displaystyle \mathbb {P} :\mathbf {Mod} _{A}\to \mathbf {Mod} _{A}}$，定义为

${\displaystyle \mathbb {P} (M)=\bigvee _{j\geq 0}M^{j}/\Sigma _{j},}$

其中

${\displaystyle M^{j}=\underbrace {M\wedge _{A}\cdots \wedge _{A}M} _{j}.}$

此函子是单子，而由该单子上的代数范畴，可以得到可交换${\displaystyle A}$代数的范畴${\displaystyle {\mathcal {C}}_{A}}$。

单子与伴随

如前文所述，任何伴随关系皆产生单子。反之，每个单子${\displaystyle T}$皆可由某个伴随关系产生，即原范畴与${\displaystyle T}$代数的艾伦伯格－摩尔范畴之间的自由－遗忘伴随

${\displaystyle T(-):{\mathcal {C}}\rightleftarrows {\mathcal {C}}^{T}:F.}$

其中，左伴随${\displaystyle T(-)}$将${\displaystyle {\mathcal {C}}}$的物件${\displaystyle x}$映到自由${\displaystyle T}$代数${\displaystyle T(x)}$，右伴随${\displaystyle F}$则将${\displaystyle T}$代数${\displaystyle (x,h)}$遗忘掉${\displaystyle h}$，变回${\displaystyle x}$。然而，通常有多组不同的伴随关系产生同样的单子，该些伴随关系组成范畴${\displaystyle \mathbf {Adj} ({\mathcal {C}},T)}$：物件是伴随关系${\displaystyle (F,G,\eta ,\varepsilon )}$使得${\displaystyle (GF,\eta ,G\varepsilon F)=(T,\eta ,\mu )}$，而态射是在${\displaystyle {\mathcal {C}}}$一侧为恒等函子的伴随关系态射。如此，艾伦伯格－摩尔范畴的自由－遗忘伴随${\displaystyle {\mathcal {C}}^{T}}$是${\displaystyle \mathbf {Adj} ({\mathcal {C}},T)}$的终物件，而始物件是克莱斯利范畴（英语：Kleisli category）${\displaystyle {\mathcal {C}}_{T}}$，定义为${\displaystyle {\mathcal {C}}^{T}}$中的自由${\displaystyle T}$代数组成的完全子范畴，即仅包含形如${\displaystyle T(x)}$的${\displaystyle T}$代数，其中${\displaystyle x}$历遍${\displaystyle {\mathcal {\mathcal {C}}}}$的物件。

单子伴随

设有伴随关系${\displaystyle (F:{\mathcal {C}}\to {\mathcal {D}},G:{\mathcal {D}}\to {\mathcal {C}},\eta ,\varepsilon )}$，对应单子为${\displaystyle T}$，则函子${\displaystyle G}$可分解为

${\displaystyle {\mathcal {D}}\xrightarrow {\tilde {G}} {\mathcal {C}}^{T}\xrightarrow {F} {\mathcal {C}},}$

其中${\displaystyle F}$是遗忘函子。换言之，对${\displaystyle {\mathcal {D}}}$中任意物件${\displaystyle Y}$，都能赋予${\displaystyle G(Y)}$自然的${\displaystyle T}$代数结构。若分解式中，首个函子${\displaystyle {\tilde {G}}}$给出${\displaystyle {\mathcal {D}}}$与${\displaystyle C^{T}}$两范畴间的等价，则形容该伴随关系为单子的（英语：monadic）。^[14]后亦引申用作形容函子，若函子${\displaystyle G:{\mathcal {D}}\to {\mathcal {C}}}$有左伴随${\displaystyle F}$，且该伴随关系为单子的，则${\displaystyle G}$亦称为单子的。例如，群范畴与集合范畴间的自由－遗忘伴随是单子的，因为相应单子${\displaystyle T}$上的${\displaystyle T}$代数是群（见前文）。一般而言，若有伴随关系${\displaystyle (F:{\mathcal {C}}\to {\mathcal {D}},G:{\mathcal {D}}\to {\mathcal {C}},\eta ,\varepsilon )}$为单子的，则单从${\displaystyle {\mathcal {C}}}$的物件及其上的${\displaystyle T}$作用，已足以重组出${\displaystyle {\mathcal {D}}}$的物件。

贝克单子性定理

主条目：贝克单子性定理（英语：Beck's monadicity theorem）

贝克单子性定理给出伴随关系在何种充要条件下为单子的。定理有以下简化版：

若满足以下三项条件：

• ${\displaystyle G}$为保守函子（英语：conservative functor），换言之，${\displaystyle G}$反映同构（英语：reflects isomorphisms），即对${\displaystyle {\mathcal {D}}}$中每一支态射，其为同构当且仅当在${\displaystyle G}$作用下的像为${\displaystyle {\mathcal {C}}}$中的同构；
• ${\displaystyle {\mathcal {C}}}$有余等化子（英语：coequalizer）；
• ${\displaystyle G}$保余等化子（英语：coequalizer）；

则${\displaystyle G}$为单子的。

例如，由紧豪斯多夫空间范畴${\displaystyle \mathbf {CHaus} }$到集合范畴${\displaystyle \mathbf {Set} }$的遗忘函子是单子的。然而，由任意拓扑空间范畴${\displaystyle \mathbf {Top} }$到集合范畴${\displaystyle \mathbf {Set} }$的遗忘函子则并非单子的，而定理中，保守函子的条件不成立，因为有非紧或非豪斯多夫空间，之间存在连续双射，但不为同胚。^[15] 贝克定理有对偶版本，刻划余单子伴随关系，对拓扑斯论及有关下降（英语：descent (category theory)）的代数几何课题有用。

余单子的伴随关系，首先有下列例子：

${\displaystyle -\otimes _{A}B:\mathbf {Mod} _{A}\rightleftarrows \mathbf {Mod} _{B}:F,}$

其中${\displaystyle A,B}$皆为交换环，左伴随用到的张量积${\displaystyle \otimes _{A}}$的定义中，选定了环同态${\displaystyle A\to B}$，而右伴随${\displaystyle F}$是遗忘函子。根据贝克定理，当且仅当${\displaystyle B}$为忠实平坦${\displaystyle A}$模时，该伴随为余单子的。所以，可将配备下降数据（英语：descent datum，即源自伴随关系的余单子的作用）的${\displaystyle B}$模，降成${\displaystyle A}$模。所得的忠实平坦下降（英语：faithfully flat descent）理论，广泛应用于代数几何。

用途

函数式编程中，会使用单子表达某类（有时有副作用的）顺序式计算，见单子 (函数式编程)。

范畴论逻辑中，藉闭包算子、内代数，以及两者与S4模态逻辑、直觉主义逻辑的关系，能以单子馀单子理论类比模态逻辑。

推广

亦可定义2-范畴${\displaystyle {\mathcal {C}}}$中的单子。

参见

• 单子间的分配律（英语：Distributive law between monads）
• 洛维尔理论（英语：Lawvere theory）
• 单子 (函数式编程)——函数式编程中，用作构造通用类型的设计模式
• 多子 (范畴论)（英语：Polyad）
• 强单子（英语：Strong monad）

参考文献

1. Barr, Michael; Wells, Charles. Toposes, Triples and Theories [拓扑斯、三元组与理论] (PDF). Grundlehren der mathematischen Wissenschaften 278 (Springer-Verlag). 1985: 82 and 120 [2021-09-17]. ISBN 0-387-96115-1. （原始内容存档 (PDF)于2020-11-25）.
2. Klin; Salamanca. Iterated Covariant Powerset is not a Monad [共变幂集迭代后不是单子]. Electronic Notes in Theoretical Computer Science. 2018-12-01, 341: 261–276. doi:10.1016/j.entcs.2018.11.013  （英语）.
3. Godement, Roger. Topologie Algébrique et Théorie des Faisceaux [代数拓扑与层论]. Actualités Sci. Ind., Publ. Math. Univ. Strasbourg 1252. Paris: Hermann. 1958: viii+283 pp （法语）. |issue=被忽略 (帮助)
4. Huber, Peter J. Homotopy theory in general categories [一般范畴的同伦论]. Mathematische Annalen. 1961, 144 (5): 361–385 （英语）.
5. Kleisli, Heinrich. Every standard construction is induced by a pair of adjoint functors [每个标准构造皆由某对伴随函子产生]. Proceedings of the American Mathematical Society. 1965, 16 (3): 544–546 （英语）.
6. Eilenberg, Samuel; Moore, John Coleman. Adjoint functors and triples [伴随函子与三元组]. Am. J. Math. 1965, 9: 301–398 （英语）.
7. Linton, Fred E. J. Some aspects of equational theories [等式理论的若干方面]. Proc. Conf. on Categorical Algebra at La Jolla. 1966: 84–95 （英语）. 参数|journal=与模板{{cite conference}}不匹配（建议改用{{cite journal}}或|book-title=） (帮助)
8. Moggi, Eugenio. Notions on computation on monads [单子上的计算概念] (PDF). [2021-09-25]. （原始内容存档 (PDF)于2011-03-22） （英语）.
9. Plotkin, Gordon; Power, John. Adequacy for Algebraic Effects [代数效果的适切性]. Proc. FOSSACS 2001. Lecture Notes in Computer Science 2030. 2001: 1–24. doi:10.1007/3-540-45315-6_1 （英语）.
10. Riehl (2017，162)
11. Świrszcz, T. Monadic functors and convexity [单子函子与凸性]. Bull. Acad. Polon. Sci. Sér. Sci. Math. Astron. Phys. 1974, 22: 39–42. MR 0390019 （英语）.
12. Jacobs, Bart. Convexity, Duality and Effects [凸性、对偶、作用]. Calude, C.S.; Sassone, V. (编). Theoretical Computer Science [理论电脑科学]. IFIP Advances in Information and Communication Technology 323. 2010: 1–19. ISBN 978-3-642-15239-9. doi:10.1007/978-3-642-15240-5_1  （英语）.
13. Basterra, M. André–Quillen cohomology of commutative S-algebras [交换S代数的André–Quillen上同调]. Journal of Pure and Applied Algebra. 1999-12-15, 144 (2): 111–143 [2021-09-18]. ISSN 0022-4049. doi:10.1016/S0022-4049(98)00051-6 . （原始内容存档于2022-01-30） （英语）.
14. MacLane (1978)所用定义中，条件“等价”要再加强为“同构（英语：Isomorphism of categories）”。
15. MacLane (1978，§§VI.3, VI.9)

• Barr, Michael; Wells, Charles. Category Theory for Computing Science [电脑科学用的范畴论] (PDF). 1999 [2021-09-24]. （原始内容存档 (PDF)于2021-12-30） （英语）.
• Kock, Anders. On Double Dualization Monads [论双重对偶单子]. Mathematica Scandinavica. 1970, 27: 151. doi:10.7146/math.scand.a-10995  （英语）.
• Leinster, Tom. Codensity and the ultrafilter monad [余密度与超滤子单子]. Theory and Applications of Categories. 2013, 28: 332–370. Bibcode:2012arXiv1209.3606L. arXiv:1209.3606  （英语）.
• MacLane, Saunders. Categories for the Working Mathematician [现职数学家用的范畴]. Graduate Texts in Mathematics 5. 1978. ISBN 978-1-4419-3123-8. doi:10.1007/978-1-4757-4721-8  （英语）.
• Pedicchio, Maria Cristina; Tholen, Walter (编). Categorical Foundations. Special Topics in Order, Topology, Algebra, and Sheaf Theory [范畴基础。序、拓扑、代数、层论特别专题]. Encyclopedia of Mathematics and Its Applications 97. Cambridge: Cambridge University Press. 2004. ISBN 0-521-83414-7. Zbl 1034.18001 （英语）.
• Riehl, Emily. Category Theory in Context [脉络中的范畴论] (PDF). 2017. ISBN 9780486820804. （原始内容存档 (PDF)于5 Apr 2021） （英语）.
• Turi, Daniele. Category Theory Lecture Notes [范畴论讲义] (PDF). 1996–2001 [2021-09-24]. （原始内容存档 (PDF)于2022-02-21） （英语）.