幺半范畴

张量范畴（tensor category），或曰幺半范畴（monoidal category）， 直觉地讲，是个配上张量积的阿贝尔范畴（abelian category），可当作环的范畴化。

定义

数学中，一个张量范畴（tensor category，或称幺半范畴 monoidal category）是一个包含单一个对象的双范畴）bicategory）。 更具体的描述：一个张量范畴是

• 一个范畴 ${\displaystyle \mathbb {C} }$;
• 被赋予张量积，即一个二元函子

${\displaystyle \otimes :\mathbb {C} \times \mathbb {C} \to \mathbb {C} }$;

• 被赋予一个单位对象 ${\displaystyle I}$;
• 被赋予三组自然同构映射：
  • 结合子${\displaystyle \alpha }$: ${\displaystyle \alpha _{A,B,C}:(A\otimes B)\otimes C\to A\otimes (B\otimes C)}$;
  • 左/右单位子: 自然同构映射 ${\displaystyle \lambda }$, ${\displaystyle \rho }$:

${\displaystyle \lambda _{A}:I\otimes A\to A}$,

${\displaystyle \rho _{A}:A\otimes I\to A}$;

• 满足以下相容条件:

每${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$, ${\displaystyle D}$ ${\displaystyle \in }$ ${\displaystyle \mathbb {C} }$,

和

都交换.///

在这以上两道相容条件下，任何以结合子,左右单位子和张量积组成的图表都交换，因为 Mac Lane 凝聚定理(Mac Lane's coherence theorem): 每个幺半范畴都 幺半等价(monoidally equivalent) 于一严格幺半范畴（见下）.

严格幺半范畴

严格幺半范畴(strict monoidal category) 是个幺半范畴 ，其自然态射 ${\displaystyle \alpha }$, ${\displaystyle \lambda }$ 和 ${\displaystyle \rho }$ 都是恒等影射.

取任一 范畴 ${\displaystyle \mathbb {C} }$, 我们可构筑其 自由严格幺半范畴 ${\displaystyle \Sigma (\mathbb {C} )}$:

• 对象：其每一对象是一串由${\displaystyle \mathbb {C} }$里面的对象组成之有限序列 ${\displaystyle (A_{1},\ldots ,A_{n}}$)；
• 态射：当且仅当${\displaystyle n=m}$时，我们在二个对象 ${\displaystyle (A_{1},\ldots ,A_{n})}$ 和 ${\displaystyle (B_{1},\ldots ,B_{m})}$ 之间定义 态射:每 ${\displaystyle \Sigma (\mathbb {C} )}$-态射 是一串由 ${\displaystyle \mathbb {C} }$-态射组成的有限序列 ${\displaystyle (f_{1}:A_{1}\to B_{1},\ldots ,f_{n}:A_{n}\to B_{n})}$ ；
• 张量积： 二个${\displaystyle \Sigma (\mathbb {C} )}$-对象${\displaystyle (A_{1},\ldots ,A_{n})}$ 及 ${\displaystyle (B_{1},\ldots ,B_{m})}$之张量积， 我们定义为 此二有限序列之串接(concatenation) ${\displaystyle (A_{1},\ldots ,A_{n},B_{1},\ldots ,B_{m})}$ ； 同样地任何二 ${\displaystyle \Sigma (\mathbb {C} )}$-态射之张量积， 我们定义为其串接。

按：此算符 ${\displaystyle \Sigma }$ ，向由任一 范畴 ${\displaystyle \mathbb {C} }$ 配上 ${\displaystyle \Sigma (\mathbb {C} )}$，可推广到 ${\displaystyle {\textbf {Cat}}}$上的严格-2-单子 （strict 2-monad）。

例

取任一范畴，若以其平常范畴积作张量积，以其终对象作单位对象，则成为一个张量范畴。 亦可取任一范畴，以其余积（co-product）作张量积，以其始对象作单位对象，亦成一个张量范畴。 （此二例实为对称幺半范畴结构。） 但亦有许多张量范畴（例如：${\displaystyle R}$-Mod，如下），其张量积 既非 范畴积 亦非 范畴余积。

以下举张量范畴二例——向量空间范畴和集合范畴——并表明其类比：

${\displaystyle R}$-Mod	Set
取任一域 或交换环 ${\displaystyle R}$, 各 ${\displaystyle R}$-模 所成之 范畴 ${\displaystyle R}$-模 (若R 为一域， 则 R-模即 R－向量空间) 是一 对称幺半范畴；其张量积 ⊗ 与单位对象为：${\displaystyle R}$.	范畴 集 为一对称幺半范畴赋有张量积 × 与单位对象 {*}.
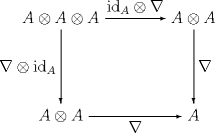
单元结合代数为${\displaystyle R}$-模之 一对象，赋上态射 ${\displaystyle \nabla :A\otimes A\rightarrow A}$ 与 ${\displaystyle \eta :R\rightarrow A}$ 并满足以下条件:	A 幺半群 为一对象 M ，配上态射 ${\displaystyle \circ :M\times M\rightarrow M}$与 ${\displaystyle 1:\{*\}\rightarrow M}$ 并满足
and	与
.	.
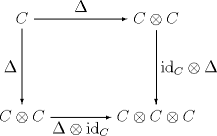
A 余代数(coalgebra) 是一个 对象 C ，被赋予 态射 ${\displaystyle \Delta :C\rightarrow C\otimes C}$ 和 ${\displaystyle \epsilon :C\rightarrow R}$ 并满足以下条件:	集内每一对象（即每一集合）S， 都被赋予 态射 ${\displaystyle \Delta :S\rightarrow S\times S}$ 和 ${\displaystyle \epsilon :S\rightarrow \{*\}}$ 满足以下条件:
and	and
.	.
	此 ε 是唯一的，因为 ${\displaystyle \{*\}}$ （即一元集合）是个终对象.

相关的结构

• 很多张量范畴更进一步有 辫, 交换态射 or 封闭等结构. 详见下述参考。
• 幺半函子（英语：monoidal functor）为二张量范畴（么半范畴）间、保存张量积结构之函子； 幺半态射为二么半函子间之态射（自然变换 (natural transformations)）。
• 一般幺半群之概念可推广成么半范畴中的幺半对象（英语：monoid object）。尤其者，可视一严格么半范畴作 范畴之“范畴” Cat中的么半对象（并以卡氏积为么半结构）。
• 上有界交半格 构成一严格对称么半范畴：其积为交，而单位元则为顶。

应用

• 么半范畴被用以定义直觉主义线性逻辑的积性部分模型。它们也是凝态物理中拓扑序的数学基础。
• 张量范畴是二维保角场论和拓扑量子场论之代数框架.

参考

• Mac Lane, Saunders (1963). "Natural Associativity and Commutativity". Rice University Studies 49, 28–46.
• Kelly, G. Max (1964). "On MacLane's Conditions for Coherence of Natural Associativities, Commutativities, etc." Journal of Algebra 1, 397–402
• Joyal, André; Street, Ross (1993). "Braided Tensor Categories". Advances in Mathematics 102, 20–78.
• Mac Lane, Saunders (1997), Categories for the Working Mathematician (2nd ed.). New York: Springer-Verlag.
• Baez, John, Definitions （页面存档备份，存于互联网档案馆）
• : <<Braided Category>>, <<Encyclopaedia of Mathematics>>,Springer On-line Reference Works （页面存档备份，存于互联网档案馆）