猜想
来自维基百科,自由的百科全书
数学中的猜想是在根据不完全信息下的结论及命题,是不知其真假的数学叙述,它可能为真,暂时未被证明或反证[1][2] 。某些猜想会称为“假设”,尤其是当它是针对某些问题提出的答案。
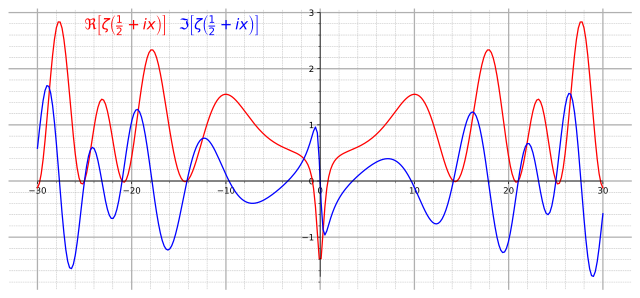
像黎曼猜想(目前仍然是猜想)或是费马最后定理(以往是猜想,一直到1995年才得证)都对数学历史带来许多的进展,而且为了证明这些猜想,也发展了新的数学领域。
当猜想被证明后,它便会成为定理。猜想只要未成为定理,数学家都要小心在逻辑结构之中使用这些猜想。猜想主要因为类比推理和偶然发现的巧合而出现。数学家通常会使用不完全归纳法,来测试自己的猜想。例如费马曾经根据首五个费马数是素数,便猜想所有费马数都是素数(此猜想已被推翻)。
猜想的解决方式
正式数学是以可以验证的事实为基础。在数学上,一个猜想不管有多少的例子支持,都无法让猜想变成定理,因为只要有一个反例立刻就可以推翻此一猜想。数学家会设法为猜想寻找反例,有时数学期刊的论文内容会提到针对猜想寻找反例的范围已经超过以往的纪录。例如考拉兹猜想内容是特定的整数数列是否会结束在特定的一个数值,已经针对268以下的所有整数进行测试。不过没有找到反证不代表反证不存在,也不代表猜想成立,有可能有极少数的反证存在,只是因为数值太大或是其他原因,尚未找到这个反证。
一个猜想只有在逻辑上不可能为误时,才能视为此一猜想成立。作法有许多种,细节可以参考证明技巧。
若猜想的可能反例只有有限多组时,有一种证明方式称为“暴力法”(brute force),就是用所有的反例一一验证,确定它们都不是反例。因为可能反例的数量可能很多,此时的暴力法可能需要配合一些实际的作法,例如用电脑算法来确认所有的可能反例都不是反例。像1976年及1977年的四色定理暴力法证明,一开始也有人质疑,最后在2005年由定理证明软件确认过结果无误。
若猜想已被证明,猜想就不再是猜想,而是定理了。有许多重要的定理是从猜想开始的,例如几何化猜想(证明了庞加莱猜想)、费马大定理等。
若已找到反例的猜想,有时会称为“假猜想”,例如波利亚猜想及欧拉猜想。
并非所有的猜想都能解决。连续统假设已被显示为不能决定(或独立)于集合论公理体系。可以将此陈述或其反例作为一个新的体系而保持一致(例如可以视平行公理或真或假)。
在这个情况,若果某个证明使用了这个陈述,研究者通常会找寻另一个不须假设的解(同样道理,想像一件诱人的事情——欧几理德几何的陈述可以只用中立几何(axioms of neutral geometry)的公理来证明,那就是没有平行公理)。除非是专注研究这个公理,研究者通常不必担心结果要不要选择公理。
参考文献
参见
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
