大斜方截半二十面体

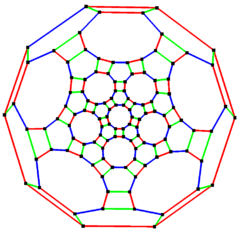
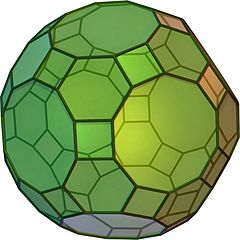
在几何学中，大斜方截半二十面体（英语：Great rhombicosidodecahedron）又称为截角截半二十面体（英语：Truncated icosidodecahedron）是一种半正多面体，由于其具有点可递的性质，因此属于阿基米德立体^[1]，是十三种由2种以上的正多边形组成的非柱体几何图形之一。

此条目的主题是一种阿基米德立体。关于同名的星形均匀多面体，请见“非凸大斜方截半二十面体”。

大斜方截半二十面体

(按这里观看旋转模型)
类别	半正多面体
对偶多面体	四角化菱形三十面体
识别
名称	大斜方截半二十面体
参考索引	U28, C31, W16
鲍尔斯缩写 （verse-and-dimensions的wikia：Bowers acronym）	grid
数学表示法
考克斯特符号 （英语：Coxeter-Dynkin diagram）
施莱夫利符号	${\displaystyle t{\begin{Bmatrix}3\\5\end{Bmatrix}}}$ tr{5,3}
威佐夫符号 （英语：Wythoff symbol）	2 3 5 |
康威表示法	bD taD
性质
面	62
边	180
顶点	120
欧拉特征数	F=62, E=180, V=120 （χ=2）
组成与布局
面的种类	正方形 正六边形 正十边形
面的布局 （英语：Face configuration）	30个{4} 20个{6} 12个{10}
顶点图	4.6.10
对称性
对称群	Ih群
特性
环带多面体
图像
4.6.10 （顶点图） 四角化菱形三十面体 （对偶多面体） （展开图）
查 论 编

大斜方截半二十面体共有62个面、180条棱和120个顶点，是凸均匀多面体中顶点数最多也是棱数最多的多面体。由于其每个面都具有点对称性（与180°的旋转对称等效），因此是一种环带多面体。

1 sources

命名

截半二十面体及其截角的结果 名称截角截半二十面体（英语：Truncated icosidodecahedron）最初由约翰内斯·开普勒给出，但这个名称有歧义，因为直接将截半二十面体透过截角变换的结果，其所形成的四边形面是一个长方形而不是正方形，然而这个立体图形在拓朴上与大斜方截半二十面体等价。 大斜方截半二十面体还有几个不同的名称： 截角截半二十面体（英语：Truncated icosidodecahedron，由约翰内斯·开普勒命名） 菱形截角截半二十面体 （英语：Rhombitruncated icosidodecahedron，由马格努斯·J·温尼尔（英语：Magnus J. Wenninger）命名[3]） 大斜方截半二十面体 （英语：Great rhombicosidodecahedron，由罗伯特·威廉斯（英语：Robert Williams (geometer)）[5]和彼得·克伦威尔（英语：Peter Cromwell）[6]命名）

5 sources

性质

由30个正方形，20个正六边形和12个正十边形组成，有120个顶点和180条棱。除棱柱和反棱柱以外，如果所有的阿基米德立体具有相同的棱长，大斜方截半二十面体将具有最大的表面积和体积。

4 sources

尺寸

若一大斜方截半二十面体的边长为a，则有下列性质：

• 体积与表面积：

  ${\displaystyle {\begin{aligned}A&=30\left[1+{\sqrt {2\left(4+{\sqrt {5}}+{\sqrt {15+6{\sqrt {6}}}}\right)}}\right]a^{2}\\&\approx 175.031045a^{2}\end{aligned}}}$^[7][8]

  ${\displaystyle {\begin{aligned}V&=(95+50{\sqrt {5}})a^{3}\approx 206.803399a^{3}\end{aligned}}}$^[7][8]

• 外接球半径

  ${\displaystyle R_{1}={\frac {a}{2}}{\sqrt {31+12{\sqrt {5}}}}\approx 3.8023945a}$^[8]，由此可知，外接球体积为${\displaystyle {\frac {4\pi {R_{1}}^{3}}{3}}}$，其值约为${\displaystyle 230.28a^{3}}$^[8]

• 内切球半径

  ${\displaystyle R_{2}={\frac {a}{2}}{\sqrt {25+10{\sqrt {5}}}}\approx 3.4409548a}$，由此可知，内切球体积为${\displaystyle {\frac {4\pi {R_{2}}^{3}}{3}}}$，其值约为${\displaystyle 170.65a^{3}}$^[8]

• 面心距
  • 正方形面心距为：${\displaystyle {\frac {\left(3+2{\sqrt {5}}\right)a}{2}}\approx 3.73606798a}$^[8]
  • 正六边形面心距为：${\displaystyle {\frac {{\sqrt {3}}(2+{\sqrt {5}})a}{2}}\approx 3.668542a}$^[8]
  • 正十边形面心距为：${\displaystyle R_{2}={\frac {a}{2}}{\sqrt {25+10{\sqrt {5}}}}\approx 3.44095a}$^[8]
• 令${\displaystyle \rho }$为大斜方截半二十面体的边心距、十二面体外接球半径为${\displaystyle b}$、正二十面体外接球半径为${\displaystyle c}$，和菱形三十面体长对角线的接球半径为${\displaystyle d}$。 存在下列等式：
  • ${\displaystyle {\frac {a}{\rho }}={\sqrt {2}}{\frac {\operatorname {tan} 18^{\circ }}{\sqrt {3}}}={\sqrt {\frac {10-4{\sqrt {5}}}{15}}}}$^[9]
  • ${\displaystyle {\frac {a}{R_{1}}}=2{\sqrt {\frac {31-12{\sqrt {5}}}{241}}}}$^[9]
  • ${\displaystyle {\frac {a}{b}}={\frac {1+{\sqrt {5}}}{10}}}$^[9]
  • ${\displaystyle {\frac {a}{c}}={\frac {{\sqrt {5}}-1}{6}}}$^[9]
  • ${\displaystyle {\frac {a}{d}}={\frac {7-{\sqrt {5}}}{22}}}$^[9]

3 sources

作法

将一个正十二面体（正二十面体）三十条棱都切一刀，在二十（十二）个顶点处也切一刀，但是要切的薄一点，就可以得到一个大斜方截半二十面体。

顶点坐标

在三维笛卡儿坐标系中，以原点为几何中心，边长2τ－2的大斜方截半二十面体的坐标是以下坐标的全偶排列^[10]：

(±1/φ, ±1/φ, ±(3 + φ)),

(±2/φ, ±φ, ±(1 + 2φ)),

(±1/φ, ±φ², ±(−1 + 3φ)),

(±(2φ − 1), ±2, ±(2 + φ)) and

(±φ, ±3, ±2φ),

其中${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}$即黄金分割率

1 sources

相关多面体与镶嵌

领结二十面体和领结十二面体的结构可以看做是大斜方截半二十面体的正方形面被分割成两个梯形[11]

大斜方截半二十面体又称为截角截半二十面体，是正二十面体截半后再经过特殊的截角变换后的结果，其他也是由正二十面体透过康威变换得到的多面体有：

正二十面体家族半正多面体

对称群: [5,3]（英语：Icosahedral symmetry）, (*532)							[5,3]+, (532)
{5,3}	t0,1{5,3}	t1{5,3}	t0,1{3,5}	{3,5}	t0,2{5,3}	t0,1,2{5,3}	s{5,3}
半正多面体对偶
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

1 sources

大斜方截半二十面体图

大斜方截半二十面体图
5阶对称性
顶点	120
边	180
半径	15
直径	15
围长	4
自同构群	120 (A5×2)
色数	2
属性	立方体（英语：Cubic graph）、 哈密顿、 正则、 零对称性（英语：Zero-symmetric graph）
查 论 编

在图论的数学领域中，与大斜方截半二十面体相关的图为大斜方截半二十面体图又称为截角截半二十面体图，是大斜方截半二十面体之边与顶点的图（英语：1-skeleton），是一种阿基米德图（英语：Archimedean graph）^[12]。

1 sources

性质

大斜方截半二十面体图与大斜方截半二十面体有相同的拓朴结构，其顶点与边的数量及结构都与阿基米德立体中的大斜方截半二十面体相同，共有120个顶点和180条边，是阿基米德图中，顶点和边数最多的图，且是一个位于零对称性（英语：Zero-symmetric graph）和立方体（英语：Cubic graph）的阿基米德图^[12]。

施莱格尔图

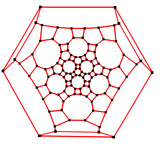3阶对称性

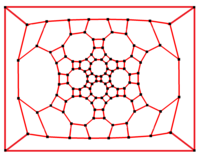2阶对称性

1 sources

参见

• 正二十面体
• 正十二面体

参考文献

1. Cromwell, P.; Polyhedra（页面存档备份，存于互联网档案馆）, CUP hbk (1997), pbk. (1999).
2. 埃里克·韦斯坦因. GreatRhombicosidodecahedron. MathWorld.、埃里克·韦斯坦因. Archimedean solid. MathWorld.
3. Klitzing, Richard. 3D convex uniform polyhedra x3x5x - grid. bendwavy.org.

1. Cromwell, P. Polyhedra. United Kingdom: Cambridge. 1997: 79–86 Archimedean solids. ISBN 0-521-55432-2.
2. Wenninger, Magnus（英语：Magnus J. Wenninger）, Polyhedron Models, Cambridge University Press, 1974, ISBN 978-0-521-09859-5, MR 0467493
3. Wenninger, (Model 16^[2], p. 30)
4. Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X.
5. Williamson^[4] (Section 3-9, p. 94)
6. Cromwell^[1] (p. 82)
7. Weisstein, Eric W. (编). Great rhombicosidodecahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
8. Harish Chandra Rajpoot. Mathematical analysis of great rhombicosidodecahedron (the largest Ar…. 2015-03-19 [2017-07-03]. （原始内容存档于2018-08-26）.
9. Robert Whittaker. The Great Rhombicosidodecahedron | polyhedra.mathmos.net. polyhedra.mathmos.net. [2017-07-11]. （原始内容存档于2016-07-04） （英语）.
10. Weisstein, Eric W. (编). Icosahedral group. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
11. Symmetrohedra: Polyhedra from Symmetric Placement of Regular Polygons （页面存档备份，存于互联网档案馆） Craig S. Kaplan
12. Read, R. C.; Wilson, R. J., An Atlas of Graphs, Oxford University Press: 269, 1998

外部链接

• 埃里克·韦斯坦因, 大斜方截半二十面体 （参阅阿基米德立体） 于MathWorld（英文）
  • 埃里克·韦斯坦因. Great rhombicosidodecahedral graph. MathWorld.
• Editable printable net of a truncated icosidodecahedron with interactive 3D view（页面存档备份，存于互联网档案馆）
• The Uniform Polyhedra（页面存档备份，存于互联网档案馆）
• Virtual Reality Polyhedra（页面存档备份，存于互联网档案馆） The Encyclopedia of Polyhedra