卷积
来自维基百科,自由的百科全书
在泛函分析中,卷积(convolution),或译为叠积、褶积或旋积,是透过两个函数和生成第三个函数的一种数学算子,表征函数与经过翻转和平移的的乘积函数所围成的曲边梯形的面积。如果将参加卷积的一个函数看作区间的指示函数,卷积还可以被看作是“移动平均”的推广。

定义
卷积是数学分析中一种重要的运算。设:和是实数上的两个可积函数,定义二者的卷积为如下特定形式的积分变换:
仍为可积函数,并且有着:
函数和,如果只支撑在之上,则积分界限可以截断为:
- 对于
对于两个得出复数值的多元实变函数,可以定义二者的卷积为如下形式的多重积分:
卷积有一个通用的工程上的符号约定[1]:
它必须被谨慎解释以避免混淆。例如:等价于,而却实际上等价于[2]。
历史
卷积运算的最早使用出现在达朗贝尔于1754年出版的《宇宙体系的几个要点研究》中对泰勒定理的推导之中[3]。还有西尔维斯特·拉克鲁瓦,将类型的表达式,用在他的1797年–1800年出版的著作《微分与级数论文》中[4]。此后不久,卷积运算出现在皮埃尔-西蒙·拉普拉斯、约瑟夫·傅里叶和西梅翁·泊松等人的著作中。这个运算以前有时叫做“Faltung”(德语中的折叠)、合成乘积、叠加积分或卡森积分[5]。
“卷积”这个术语早在1903年就出现了,然而其定义在早期使用中是相当生僻的[6][7],直到1950年代或1960年代之前都未曾广泛使用。
简介
如果和都是在Lp 空间内的勒贝格可积函数,则二者的卷积存在,并且在这种情况下也是可积的[8]。这是托内利定理的结论。对于在中的函数在离散卷积下,或更一般的对于在任何群的上的卷积,这也是成立的。同样的,如果而,这里的,则,并且其Lp 范数间有着不等式:
在的特殊情况下,这显示出是在卷积下的巴拿赫代数(并且如果和几乎处处非负则两边间等式成立)。
卷积与傅里叶变换有着密切的关系。例如两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换,利用此一性质,能简化傅里叶分析中的许多问题。
由卷积得到的函数,一般要比和都光滑。特别当为具有紧支集的光滑函数,为局部可积时,它们的卷积也是光滑函数。利用这一性质,对于任意的可积函数,都可以简单地构造出一列逼近于的光滑函数列,这种方法称为函数的光滑化或正则化。
这里的叫做移位(displacement)或滞后(lag)。
对于单位脉冲函数和某个函数,二者得到的卷积就是本身,此被称为冲激响应:
在连续时间线性非时变系统中,输出信号被描述为输入信号与冲激响应的卷积[9]:
两个独立的随机变量和,每个都有一个概率密度函数,二者之和的概率密度,是它们单独的密度函数的卷积:
图解
|

|
| 两个矩形脉冲波的卷积。其中函数首先对反射,接着平移,成为。那么重叠部分的面积就相当于处的卷积,其中横坐标代表待变量以及新函数的自变量。 | 
|
| 矩形脉冲波和指数衰减脉冲波的卷积(后者可能出现于RC电路中),同样地重叠部分面积就相当于处的卷积。注意到因为是对称的,所以在这两张图中,反射并不会改变它的形状。 | 
|
周期卷积
这里的是任意参数。
任何可积分函数,都可以通过求函数的所有整数倍的平移的总和,从而制作出具有周期的周期函数 ,这叫做周期求和:
对于无周期函数与,其周期的周期求和分别是与,与的周期卷积,可以定义为与的常规卷积,或与的常规卷积,二者都等价于与的周期积分:
圆周卷积是周期卷积的特殊情况[11][12],其中函数和二者的非零部分,都限定在区间之内,此时的周期求和称为“周期延拓”。中函数可以通过取非负余数的模除运算表达为“圆周函数”:
而积分的界限可以缩简至函数的长度范围:
离散卷积

对于定义在整数上且得出复数值的函数和,离散卷积定义为[13]:
这里一样把函数定义域以外的值当成零,所以可以扩展函数到所有整数上(如果本来不是的话)。两个有限序列的卷积的定义,是将这些序列扩展成在整数集合上有限支撑的函数。在这些序列是两个多项式的系数之时,这两个多项式的普通乘积的系数,就是这两个序列的卷积。这叫做序列系数的柯西乘积。
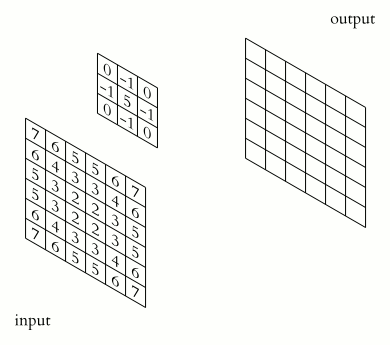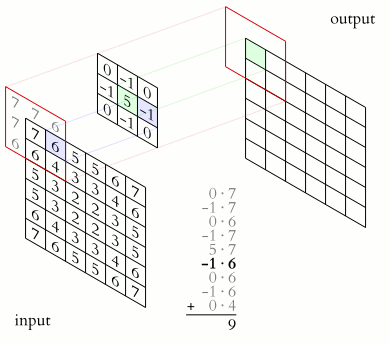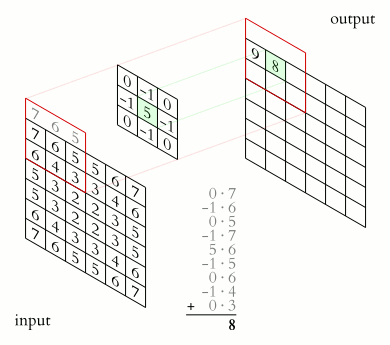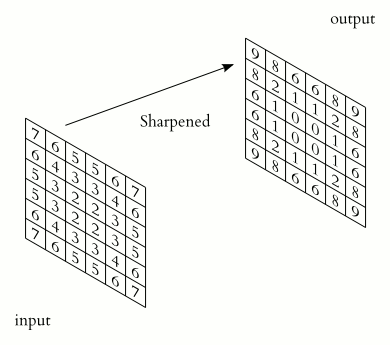
类似于一维情况,使用星号表示卷积,而维度体现在星号的数量上,维卷积就写为个星号。下面是维信号的卷积的表示法:
对于离散值的信号,这个卷积可以直接如下这样计算:
结果的离散多维卷积所支撑的输出区域,基于两个输入信号所支撑的大小和区域来决定。

对于离散序列和一个参数,无周期函数和的“周期卷积”是为:
这个函数有周期,它有最多个唯一性的值。和的非零范围都是的特殊情况叫做圆周卷积:
离散圆周卷积可简约为矩阵乘法,这里的积分变换的核函数是循环矩阵:
性质
各种卷积算子都满足下列性质:
- 数乘结合律
- 复数共轭
- 微分有关
- 积分有关
- 如果,并且,则有:
如果和是可积分函数,则它们在整个空间上的卷积的积分,简单的就是它们积分的乘积[14]:
在一元函数情况下,和的卷积的导数有着:
这里的是微分算子。更一般的说,在多元函数的情况下,对偏导数也有类似的公式:
这就有了一个特殊结论,卷积可以看作“光滑”运算:和的卷积可微分的次数,是和的总数。
这些恒等式成立的严格条件,为和是绝对可积分的,并且至少二者之一有绝对可积分()弱导数,这是Young卷积不等式的结论。
卷积定理
卷积定理指出[15],在适当的条件下,两个函数(或信号)的卷积的傅里叶变换,是它们的傅里叶变换的逐点乘积。更一般的说,在一个域(比如时域)中的卷积等于在其他域(比如频域)逐点乘法。
设两个函数和,分别具有傅里叶变换和:
卷积定理声称:
应用逆傅里叶变换产生推论:
这里的算符指示逐点乘法。
这一定理对拉普拉斯变换、双边拉普拉斯变换、Z变换、梅林变换和Hartley变换等各种傅里叶变换的变体同样成立。在调和分析中还可以推广到在局部紧致的阿贝尔群上定义的傅里叶变换。
对于周期为的函数和,可以被表达为二者的周期求和:
逐点乘积的周期也是,它的傅里叶级数系数为:
周期卷积的周期也是,周期卷积的卷积定理为:
对于作为两个连续函数采样的序列和,它们具有离散时间傅里叶变换和:
这里的算子指示离散时间傅里叶变换(DTFT)。
离散卷积的卷积定理为:
对于周期为的序列和:
相较于离散时间傅里叶变换和的周期是,它们是按间隔采样和,并在个采样上进行了逆离散傅里叶变换(DFT-1或IDFT)的结果。
离散周期卷积的周期也是。离散周期卷积定理为:
这里的算子指示长度的离散傅里叶变换(DFT)。
它有着推论:
对于其非零时段小于等于的和,离散圆周卷积的卷积定理为:
推广
卷积的概念还可以推广到数列、测度以及广义函数上去。函数是定义在上的可测函数(measurable function),与存在卷积并记作。如果函数不是定义在上,可以把函数定义域以外的值都规定成零,这样就变成一个定义在上的函数。
若G是有某m 测度的群(例如豪斯多夫空间上哈尔测度下局部紧致的拓扑群),对于G上m-勒贝格可积的实数或复数函数f和g,可定义它们的卷积:
离散卷积的计算方法
计算卷积有三种主要的方法,分别为
- 直接计算(Direct Method)
- 快速傅里叶变换(FFT)
- 分段卷积(sectioned convolution)
方法1是直接利用定义来计算卷积,而方法2和3都是用到了FFT来快速计算卷积。也有不需要用到FFT的作法,如使用数论变换。
- 作法:利用卷积的定义
- 若和皆为实数信号,则需要个乘法。
- 若和皆为更一般性的复数信号,不使用复数乘法的快速算法,会需要个乘法;但若使用复数乘法的快速算法,则可简化至个乘法。
- 因此,使用定义直接计算卷积的复杂度为。
- 概念:由于两个离散信号在时域(time domain)做卷积相当于这两个信号的离散傅里叶变换在频域(frequency domain)做相乘:
- ,可以看出在频域的计算较简单。
- 作法:因此这个方法即是先将信号从时域转成频域:
- ,于是
- ,最后再将频域信号转回时域,就完成了卷积的计算:
- 总共做了2次DFT和1次IDFT。
- 特别注意DFT和IDFT的点数要满足。
- 由于DFT有快速算法FFT,所以运算量为
- 假设点DFT的乘法量为,和为一般性的复数信号,并使用复数乘法的快速算法,则共需要个乘法。
总结
视角
- 概念:将切成好几段(section),每一段分别和做卷积后,再将结果相加。
- 作法:先将切成每段长度为的区段(),假设共切成S段:
- Section 1:
- Section 2:
- Section r:
- Section S:
- ,为各个section的和
- 。
- 因此,
- ,
- 每一小段作卷积则是采用方法2,先将时域信号转到频域相乘,再转回时域:
- 。
- 总共只需要做点FFT 次,因为只需要做一次FFT。
- 假设点DFT的乘法量为,和为一般性的复数信号,并使用复数乘法的快速算法,则共需要个乘法。
- 运算量:
- 运算复杂度:,和呈线性,较方法2小。
- 分为 Overlap-Add 和 Overlap-Save 两种方法。
分段卷积: Overlap-Add
欲做的分段卷积分, 长度为 , 长度为 ,
Step 1: 将每 分成一段
Step 2: 再每段 点后面添加 个零,变成长度
Step 3: 把 添加 个零,变成长度 的
Step 4: 把每个 的小段和 做快速卷积,也就是,每小段会得到长度 的时域信号
Step 5: 放置第 个小段的起点在位置 上,
Step 6: 会发现在每一段的后面 点有重叠,将所有点都相加起来,顾名思义 Overlap-Add,最后得到结果
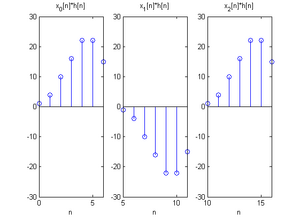
举例来说:
, 长度
, 长度
令
-
x[n]和h[n]
令 切成三段,分别为 , 每段填 个零,并将 填零至长度
-
分段x[n]
将每一段做
-
分段运算结果
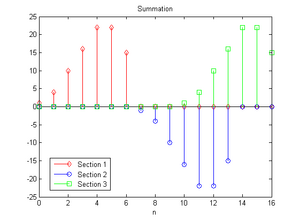
若将每小段摆在一起,可以注意到第一段的范围是 ,第二段的范围是 ,第三段的范围是 ,三段的范围是有重叠的
-
合并分段运算结果
最后将三小段加在一起,并将结果和未分段的卷积做比较,上图是分段的结果,下图是没有分段并利用快速卷积所算出的结果,验证两者运算结果相同。
-
结果比较图
分段卷积: Overlap-Save
欲做的分段卷积分, 长度为 , 长度为 ,
Step 1: 将 前面填 个零
Step 2: 第一段 , 从新的 中 取到 总共 点当做一段,因此每小段会重复取到前一小段的 点,取到新的一段全为零为止
Step 3: 把 添加 个零,变成长度 的
Step 4: 把每个 的小段和 做快速卷积,也就是,每小段会得到长度 的时域信号
Step 5: 对于每个 小段,只会保留末端的 点,因此得名 Overlap-Save
Step 6: 将所有保留的点合再一起,得到最后结果
举例来说:
, 长度
, 长度
令
-
x[n]和h[n]
将 前面填 个零以后,按照 Step 2 的方式分段,可以看到每一段都重复上一段的 点
-
分段x[n]
再将每一段做 以后可以得到
-
分段运算结果
保留每一段末端的 点,摆在一起以后,可以注意到第一段的范围是 ,第二段的范围是 ,第三段的范围是 ,第四段的范围是 ,四段的范围是没有重叠的
-
合并分段运算结果
将结果和未分段的卷积做比较,下图是分段的结果,上图是没有分段并利用快速卷积所算出的结果,验证两者运算结果相同。
-
结果比较图
至于为什么要把前面 丢掉?
以下以一例子来阐述:
, 长度 ,
, 长度 ,
第一条蓝线代表 轴,而两条蓝线之间代表长度 ,是在做快速卷积时的周期
-
x[n]和h[n]
当在做快速卷积时,是把信号视为周期 ,在时域上为循环卷积分,
而在一开始前 点所得到的值,是 和 内积的值,
然而 这 个值应该要为零,以往在做快速卷积时长度为 时不会遇到这些问题,
而今天因为在做快速卷积时长度为 才会把这 点算进来,因此我们要丢弃这 点内积的结果
-
循环卷积
为了要丢弃这 点内积的结果,位移 点,并把位移以后内积合的值才算有效。
-
位移以后内积
以上三种方法皆可用来计算卷积,其差别在于所需总体乘法量不同。基于运算量以及效率的考量,在计算卷积时,通常会选择所需总体乘法量较少的方法。
以下根据和的长度()分成5类,并列出适合使用的方法:
- 为一非常小的整数 - 直接计算
- - 分段卷积
- - 快速傅里叶变换
- - 分段卷积
- 为一非常小的整数 - 直接计算
基本上,以上只是粗略的分类。在实际应用时,最好还是算出三种方法所需的总乘法量,再选择其中最有效率的方法来计算卷积。
Q1:当,适合用哪种方法计算卷积?
Ans:
- 方法1:所需乘法量为
- 方法2:,而2016点的DFT最少乘法数,所以总乘法量为
- 方法3:
- 若切成8块(),则。选,则总乘法量为,比方法1和2少了很多。
- 但是若要找到最少的乘法量,必须依照以下步骤
- (1)先找出:解 :
- (2)由算出点数在附近的DFT所需最少的乘法量,选择DFT的点数
- (3)最后由算出
- 因此,
- (1)由运算量对的偏微分为0而求出
- (2),所以选择101点DFT附近点数乘法量最少的点数或。
- (3-1)当,总乘法量为。
- (3-2)当,总乘法量为。
- 由此可知,切成20块会有较好的效率,而所需总乘法量为21480。
- 因此,当,所需总乘法量:分段卷积<快速傅里叶变换<直接计算。故,此时选择使用分段卷积来计算卷积最适合。
Q2:当,适合用哪种方法计算卷积?
Ans:
- 方法1:所需乘法量为
- 方法2:,选择1026点DFT附近点数乘法量最少的点数,。
- 因此,所需乘法量为
- 方法3:
- (1)由运算量对的偏微分为0而求出
- (2),所以选择7点DFT附近点数乘法量最少的点数或或。
- (3-1)当,总乘法量为。
- (3-2)当,总乘法量为。
- (3-3)当,总乘法量为。
- 由此可知,切成171块会有较好的效率,而所需总乘法量为5476。
- 因此,当,所需总乘法量:分段卷积<直接计算<快速傅里叶变换。故,此时选择使用分段卷积来计算卷积最适合。
- 虽然当是个很小的正整数时,大致上适合使用直接计算。但实际上还是将3个方法所需的乘法量都算出来,才能知道用哪种方法可以达到最高的效率。
Q3:当,适合用哪种方法计算卷积?
Ans:
- 方法1:所需乘法量为
- 方法2:,选择1026点DFT附近点数乘法量最少的点数,。
- 因此,所需乘法量为
- 方法3:
- (1)由运算量对的偏微分为0而求出
- (2),所以选择1623点DFT附近点数乘法量最少的点数。
- (3)当,总乘法量为。
- 由此可知,此时切成一段,就跟方法2一样,所需总乘法量为44232。
- 因此,当,所需总乘法量:快速傅里叶变换 = 分段卷积<直接计算。故,此时选择使用分段卷积来计算卷积最适合。
应用

卷积在科学、工程和数学上都有很多应用:
参见
引用
延伸阅读
外部链接
Wikiwand - on
Seamless Wikipedia browsing. On steroids.











![{\displaystyle [0,\infty ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/52088d5605716e18068a460dec118214954a68e9)


















































![{\displaystyle \tau \notin [0,1.5]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/838205ce42d577093b941bc0a0fe5bcfef0b8f9c)

















![{\displaystyle [0,T]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/35ccef2d3dc751e081375d51c111709d8a1d7ac6)





![{\displaystyle f[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b176b3dbcced447341ad5ab70001ef0e3231062e)
![{\displaystyle g[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3c5e1d771a2385e9aeb71838a40425bb07c89525)
![{\displaystyle (f*g)[n]\ \ \triangleq \ \sum _{m=-\infty }^{\infty }{f[m]g[n-m]}=\sum _{m=-\infty }^{\infty }f[n-m]\,g[m]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2bd9a55083d6a0d0aa8bda67d179ebc0c7970166)

![{\displaystyle (f*g)[n]=\sum _{m=-M}^{M}f[n-m]g[m]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/f0a31f12e6771e6a8b1868f15214e43c8714c1d9)





![{\displaystyle (h*x_{_{N}})[n]\ \triangleq \ \sum _{m=-\infty }^{\infty }h[m]\underbrace {x_{_{N}}[n-m]} _{\sum _{k=-\infty }^{\infty }x[n-m-kN]}\ =\ \sum _{m=0}^{N-1}\left(\sum _{k=-\infty }^{\infty }{h}[m-kN]\right)x_{_{N}}[n-m]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/14cb0408cb58e39c596cab8ee9f1f63cb6e2fa3d)
![{\displaystyle [0,N-1]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5d4099dcd12fea62ad089a8d26d2a14c54fc88f5)
![{\displaystyle (h*x_{_{N}})[n]=\sum _{m=0}^{N-1}h[m]x_{_{N}}[n-m]=\sum _{m=0}^{N-1}h[m]x[(n-m)_{\bmod {N}}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ac37f1cfe50298bfdefdcd870a5627ef30db1cee)















=f(n+1)-f(n)}](http://wikimedia.org/api/rest_v1/media/math/render/svg/10ef9708b32ccda9a3be9ff9c1f8865c4107cf59)
















![{\displaystyle {\begin{aligned}G[k]&\triangleq {\mathcal {F}}\{g_{_{P}}\}[k]={\frac {1}{P}}\int _{P}g_{_{P}}(x)e^{-i2\pi kx/P}\,dx,\quad k\in \mathbb {Z} \\H[k]&\triangleq {\mathcal {F}}\{h_{_{P}}\}[k]={\frac {1}{P}}\int _{P}h_{_{P}}(x)e^{-i2\pi kx/P}\,dx,\quad k\in \mathbb {Z} \end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3ff5ff5748d540ed77192958f5ec50cbe83ff9b2)

![{\displaystyle {\mathcal {F}}\{g_{_{P}}\cdot h_{_{P}}\}[k]=(G*H)[k]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ec23600fe822e18dc005e7025b45caeb30a17f48)

![{\displaystyle {\mathcal {F}}\{g_{_{P}}*h\}[k]=\ P\cdot G[k]\ H[k]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/6d08db60e83b8282a9c6351dc2b556632ad6c336)
![{\displaystyle h[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/89981bbbb05ffd469eeadb828c18359965985e46)
![{\displaystyle {\begin{aligned}G(s)&\triangleq {\mathcal {F}}\{g\}(s)=\sum _{n=-\infty }^{\infty }g[n]\cdot e^{-i2\pi sn}\;,\quad s\in \mathbb {R} \\H(s)&\triangleq {\mathcal {F}}\{h\}(s)=\sum _{n=-\infty }^{\infty }h[n]\cdot e^{-i2\pi sn}\;,\quad s\in \mathbb {R} \end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0173c3574eda0d0a0ab15d8aef57be616c6efd03)

![{\displaystyle g_{_{N}}[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/30368575be97a3a4a9213a5bace7faff1a4a6371)
![{\displaystyle h_{_{N}}[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/50abe51c291125077df860525b4c6c1c8d767595)
![{\displaystyle {\begin{aligned}g_{_{N}}[n]\ &\triangleq \sum _{m=-\infty }^{\infty }g[n-mN],\quad m,n\in \mathbb {Z} \\h_{_{N}}[n]\ &\triangleq \sum _{m=-\infty }^{\infty }h[n-mN],\quad m,n\in \mathbb {Z} \end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4a06f5589438df8b4574b428b5869c5178b9d2e7)


![{\displaystyle (g_{_{N}}*h)[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b3f3e5554f1c3fe2b5f2edeff4e779ccedb445a6)
![{\displaystyle {\mathcal {F}}\{g_{_{N}}*h\}[k]=\ \underbrace {{\mathcal {F}}\{g_{_{N}}\}[k]} _{G(k/N)}\cdot \underbrace {{\mathcal {F}}\{h_{_{N}}\}[k]} _{H(k/N)},\quad k,n\in \mathbb {Z} }](http://wikimedia.org/api/rest_v1/media/math/render/svg/88f84f790337809a2e0ba2a745b25083a4f3129c)
![{\displaystyle (g_{_{N}}*h)[n]=\ {\mathcal {F}}^{-1}\{{\mathcal {F}}\{g_{_{N}}\}\cdot {\mathcal {F}}\{h_{_{N}}\}\}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ab487693fbf66da441eb710125e5ceff2194398e)
![{\displaystyle (g_{_{N}}*h)[n]=\ {\mathcal {F}}^{-1}\{{\mathcal {F}}\{g\}\cdot {\mathcal {F}}\{h\}\}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a0defba14a548128651067acefb5121ba77e020c)



![{\displaystyle f[n]*g[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/53f78eb841159a85c00fe9a4331825a77341e67c)
![{\displaystyle y[n]=f[n]*g[n]=\sum _{m=0}^{M-1}f[n-m]g[m]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1081139aae46ebd7421e11ec20351dc12688cedd)




![{\displaystyle y[n]=f[n]*g[n]\leftrightarrow Y[f]=F[f]G[f]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/27f83ca717dff1b21da43e56127c50874843b8b0)
![{\displaystyle F[f]=DFT_{P}(f[n]),G[f]=DFT_{P}(g[n])}](http://wikimedia.org/api/rest_v1/media/math/render/svg/af332366ed1070784c006329adcd40833e64c44d)
![{\displaystyle Y[f]=DFT_{P}(f[n])DFT_{P}(g[n])}](http://wikimedia.org/api/rest_v1/media/math/render/svg/93ec9e3130dcd720d4d6b1930bd492f29fee0faf)
![{\displaystyle y[n]=IDFT_{P}{DFT_{P}(f[n])DFT_{P}(g[n])}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/adc12d1e8c9712ca85bf040d7e8573842c545588)





\to f_{1}[n],f_{2}[n],f_{3}[n],...,f_{S}[n](S=\left\lceil {\frac {N}{L}}\right\rceil )}](http://wikimedia.org/api/rest_v1/media/math/render/svg/6b2758eba65ad177619e0d9198cc913abf649b9a)
![{\displaystyle f_{1}[n]=f[n],n=0,1,...,L-1}](http://wikimedia.org/api/rest_v1/media/math/render/svg/22401ad12747eb80e3ec79d0c5b189b3c186d912)
![{\displaystyle f_{2}[n]=f[n+L],n=0,1,...,L-1}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ccb4f0b33490a5fc67f57cb6d353087f35c3db5d)

![{\displaystyle f_{r}[n]=f[n+(r-1)L],n=0,1,...,L-1}](http://wikimedia.org/api/rest_v1/media/math/render/svg/f0d987ef3bab08edc0d97642435c8f97a1383304)
![{\displaystyle f_{S}[n]=f[n+(S-1)L],n=0,1,...,L-1}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b30b353213c930583b0b65c5598ea334fdfee777)
![{\displaystyle f[n]=\sum _{r=1}^{S}f_{r}[n+(r-1)L]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/8ad8dbc7f1039ba3824c87225b58895e27a85453)
![{\displaystyle y[n]=f[n]*g[n]=\sum _{r=1}^{S}\sum _{m=0}^{M-1}f_{r}[n+(r-1)L-m]g[m]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e15254f6bff4b4db4f6899f0bb3e450f75e3625d)
![{\displaystyle y[n]=IDFT(\sum _{r=1}^{S}\sum _{m=0}^{M-1}DFT_{P}(f_{r}[n+(r-1)L-m])DFT_{P}(g[m])),P\geq M+L-1}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b3c1ccb338a07511f8c82bbe1478beb62fafdea6)


![{\displaystyle {\frac {N}{L}}3(L+M-1)[\log _{2}(L+M-1)+1]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e4b5d72adc35b450cfcc40c0d13720fa6d6bd070)

![{\displaystyle x[n]*h[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7c97358d336f2e21de7913bc46fac6477eef3bc6)
![{\displaystyle x[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/864cbbefbdcb55af4d9390911de1bf70167c4a3d)



![{\displaystyle h'[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7af9a0c1d0c9753adba0e2e13fc2c45e8d5698f7)
![{\displaystyle IDFT_{L+M-1}\{{DFT_{L+M-1}(x[n])DFT_{L+M-1}(h'[n])}\}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/71884e63653a1501f77c376b182141bd9d8e86ce)



![{\displaystyle x[n]=[1,2,3,4,5,-1,-2,-3,-4,-5,1,2,3,4,5]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/98580fd364a838db6ecc3c27068105c31f81d9a9)

![{\displaystyle h[n]=[1,2,3]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/67fdc55efaef23389bacd0b58cf59865377f46f4)



![{\displaystyle x_{0}[n],x_{1}[n],x_{2}[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1d11383cb60875adb6faaedbf729e5956982bff0)









![{\displaystyle IDFT_{L}\{{DFT_{L}(x[n])DFT_{L}(h'[n])}\}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7c639c720d3a6a4922220ac66a9c31d6e8eb7987)

![{\displaystyle x[n]=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/f54af19067aacc4ba29d8c5a4e661d92c3f2ab24)










![{\displaystyle x[n]=[1,2,3,4,5,6,7,8,9,10]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/197c03fad73159099a753aa21015d7a410c619ba)

![{\displaystyle h[n]=[1,2,3,4,5]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/01382de68d6838f4a938ab33a5ad465fa1ae6d0f)



![{\displaystyle h[0],h[6],h[7],h[8],h[9]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3c2e1f7ce57e74223a3049d5d803bd8af91b8019)
![{\displaystyle x[0],x[6],x[7],x[8],x[9]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5f004d095726b6a642d26dd6dc4bef9660ec8c17)
![{\displaystyle h[6],h[7],h[8],h[9]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3ccee59494bedbceae16aa4bce150fbcef8b2cf1)

![{\displaystyle h[-n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2160e2740fe612954bc0c6d78203d595d29076e3)














![{\displaystyle {\frac {\partial {{\frac {N}{L}}3(L+M-1)[\log _{2}(L+M-1)+1]}}{\partial L}}=0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5212be896bcbc7febbe5e992d9650c2b0ea09c6a)


































