二面体群

在数学中，二面体群 ${\displaystyle D_{2n}}$ 是正 ${\displaystyle n}$ 边形的对称群，具有 ${\displaystyle 2n}$ 个元素。某些书上则记为 ${\displaystyle D_{n}}$。除了 ${\displaystyle n=2}$ 的情形外，${\displaystyle D_{2n}}$ 都是非交换群。

雪花有正六边形的二面体对称。

群论
群
基本概念 子群 · 正规子群 · 商群 · 群同态 · 像 · (半)直积 · 直和 单群 · 有限群 · 无限群 · 拓扑群 · 群概形 · 循环群 · 幂零群 · 可解群 · 圈积 离散群 有限单群分类 循环群 Zn 交错群 An 李型群 散在群 马蒂厄群 M11..12,M22..24 康威群 Co1..3 扬科群 J1..4 费歇尔群（英语：Fischer group）F22..24 子魔群（英语：sub monster group） B 魔群 M 其他有限群 对称群, Sn 二面体群, Dn 无限群 整数, Z 模群, PSL(2,Z) 和 SL(2,Z) 连续群 李群 一般线性群 GL(n) 特殊线性群 SL(n) 正交群 O(n) 特殊正交群 SO(n) 酉群 U(n) 特殊酉群 SU(n) 辛群 Sp(n) G2 F4 E6 E7 E8 劳仑兹群 庞加莱群 无限维群 共形群 微分同胚群 环路群 量子群 O(∞) SU(∞) Sp(∞) 代数群 椭圆曲线 线性代数群（英语：Linear algebraic group） 阿贝尔簇（英语：Abelian variety）
查 论 编

生成元与关系

抽象言之，首先考虑 ${\displaystyle n}$ 阶循环群 ${\displaystyle C_{n}}$。反射 ${\displaystyle \tau :x\mapsto x^{-1}}$ 是 ${\displaystyle C_{n}}$ 上的自同构，而且 ${\displaystyle \tau ^{2}={\rm {id}}}$。定义二面体群为半直积

${\displaystyle D_{2n}=C_{n}\rtimes \{e,\tau \}}$

任取 ${\displaystyle C_{n}}$ 的生成元 ${\displaystyle \sigma }$，${\displaystyle D_{2n}}$ 由 ${\displaystyle \sigma ,\tau }$ 生成，其间的关系是

${\displaystyle \sigma ^{n}=e,\tau ^{2}=e,\tau \sigma \tau =\sigma ^{-1}\,}$

${\displaystyle D_{2n}}$ 的元素均可唯一地表成 ${\displaystyle \sigma ^{k}\tau ^{h}}$，其中 ${\displaystyle 0\leq k<n}$，${\displaystyle h=0,1\,}$。

几何诠释

n=5 的情形：反射对称

n=5 的情形：旋转对称

二面体群也可以诠释为二维正交群 ${\displaystyle O(2)}$ 中由

${\displaystyle \sigma :={\begin{pmatrix}\cos {2\pi \over n}&-\sin {2\pi \over n}\\\sin {2\pi \over n}&\cos {2\pi \over n}\end{pmatrix}}}$ （旋转 ${\displaystyle {\frac {2\pi }{n}}}$ 弧度）

${\displaystyle \tau :={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}}$ （对 x 轴反射）

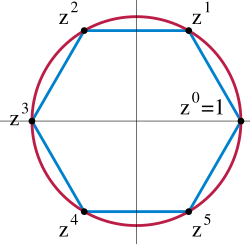
生成的子群。由此不难看出 ${\displaystyle D_{2n}}$ 是正 n 边形的对称群。

性质

• ${\displaystyle D_{2n}}$ 的中心在 ${\displaystyle n}$ 为奇数时是 ${\displaystyle \{e\}}$，在 ${\displaystyle n}$ 为偶数时是 ${\displaystyle \{e,\sigma ^{n/2}\}}$。
• 当 ${\displaystyle n}$ 为奇数时，${\displaystyle D_{4n}}$ 同构于 ${\displaystyle D_{2n}}$ 与二阶循环群的直积。同构可由下式给出：

${\displaystyle \sigma ^{k+\epsilon n}\tau ^{h}\mapsto (\sigma ^{k}\tau ^{h},\epsilon )}$

其中 ${\displaystyle h,\epsilon =0,1}$，${\displaystyle 0\leq k<n}$。

• 当 ${\displaystyle n}$ 为奇数时，${\displaystyle D_{2n}}$ 的所有反射（即：二阶元素）彼此共轭；当 ${\displaystyle n}$ 为偶数，则反射元在共轭作用下分解成两个轨道；从几何方面解释，二者差意在于反射面是否通过正 ${\displaystyle n}$ 边形的顶点。
• 若 ${\displaystyle m|n}$，则 ${\displaystyle D_{2m}\leq D_{2n}}$，由此可导出 ${\displaystyle D_{2n}}$ 共有 ${\displaystyle d(n)+\sigma (n)}$ 个子群，其中的算术函数 ${\displaystyle d(n)}$ 与 ${\displaystyle \sigma (n)}$ 分别代表 ${\displaystyle n}$ 的正因数个数与正因数之和。

表示

当 ${\displaystyle n}$ 为奇数时，${\displaystyle D_{n}}$ 有两个一维不可约表示：

${\displaystyle \tau \mapsto (-1)^{k},\;\sigma \mapsto 1\quad (k=0,1)}$

当 ${\displaystyle n}$ 为偶数时，${\displaystyle D_{n}}$ 有四个一维不可约表示：

${\displaystyle e}$

${\displaystyle \sigma }$

${\displaystyle \sigma ^{2}}$

${\displaystyle \sigma ^{3}}$

${\displaystyle \sigma ^{4}}$

${\displaystyle \sigma ^{5}}$

${\displaystyle \sigma ^{6}}$

${\displaystyle \sigma ^{7}}$

${\displaystyle \tau }$

${\displaystyle \sigma \tau }$

${\displaystyle \sigma ^{2}\tau }$

${\displaystyle \sigma ^{3}\tau }$

${\displaystyle \sigma ^{4}\tau }$

${\displaystyle \sigma ^{5}\tau }$

${\displaystyle \sigma ^{6}\tau }$

${\displaystyle \sigma ^{7}\tau }$

正八边形的停车标志在${\displaystyle D_{8}}$的群作用下的结果

${\displaystyle \tau \mapsto (-1)^{k},\sigma \mapsto (-1)^{h}\quad (k,h=0,1)}$

其余不可约表示皆为二维，共有 ${\displaystyle \lfloor n/2\rfloor }$ 个，形如下式：

${\displaystyle \sigma \mapsto {\begin{pmatrix}\omega ^{h}&0\\0&\omega ^{-h}\end{pmatrix}}\;\tau \mapsto {\begin{pmatrix}0&-1\\-1&0\end{pmatrix}}}$

其中 ${\displaystyle \omega }$ 是任一 n 次本原单位根，${\displaystyle h}$ 过 ${\displaystyle \mathbb {Z} /n\mathbb {Z} }$。由 ${\displaystyle h_{1},h_{2}}$ 给出的表示相等价当且仅当 ${\displaystyle h_{1}+h_{2}\equiv 0\mod n}$。

文献