線圖

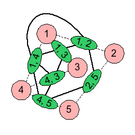
在圖論中，圖${\displaystyle G}$所對應的線圖是一張能夠反映${\displaystyle G}$中各邊鄰接性的圖，記作${\displaystyle L(G)}$。簡單來說，${\displaystyle L(G)}$將${\displaystyle G}$中的每條邊各自抽象成一個頂點；如若原圖中兩條邊相鄰，那麼就給線圖中對應頂點之間連接一條邊。因為線圖將原圖的邊化作了頂點，所以也可以將其視作原圖的一種對偶。

哈斯勒·惠特尼證明了：假定圖${\displaystyle G}$是連通的，那麼除了一種特殊情況外，我們總能根據線圖${\displaystyle L(G)}$的結構還原出${\displaystyle G}$的結構^[1]。以該定理為中介，可以證明線圖的許多其它性質。線圖總是無爪圖，即線圖的所有導出子圖均不是${\displaystyle K_{1,3}}$。

正式定義

圖${\displaystyle G}$的線圖${\displaystyle L(G)}$定義如下：

• ${\displaystyle L(G)}$的一個頂點對應${\displaystyle G}$的一邊

• ${\displaystyle L(G)}$的頂點相鄰若且唯若它們在${\displaystyle G}$對應的邊相鄰（有公共頂點）。

該定義也可以用圖論的語言表述如下：設${\displaystyle G=(V,E)}$，那麼${\displaystyle L(G)=(E,{\tilde {E}})}$，且${\displaystyle (e_{1},e_{2})\in {\tilde {E}}\iff e_{1}\cap e_{2}\neq \emptyset }$。

例子

下面的例子演示了由原圖生成線圖的流程。

• 
  原圖
• 
  製作線圖的過程
• 
  結果

性質

有些圖總不是線圖

由原圖轉移過來的性質

根據線圖的定義，若性質／概念P僅取決於原圖${\displaystyle G}$中邊的鄰接性，那麼P便可以轉移（或者說對偶）到線圖${\displaystyle L(G)}$上去變成性質／概念P'，刻畫線圖頂點的鄰接屬性。例如，圖${\displaystyle G}$中的一個匹配指的是圖中一組不相交的邊，把這一概念平移到線圖上去，就等價於線圖的一組不相鄰的頂點——用術語來說即線圖上的一個獨立集。

下面就列舉了原圖和線圖之間的若干聯繫：

• 若原圖是連通的，線圖也是。
• 若兩個圖同構，那麼它們的線圖也同構。
• 若${\displaystyle G}$的頂點數和邊數分別為${\displaystyle n}$和${\displaystyle m}$，那麼${\displaystyle L(G)}$的頂點數和邊數分別是${\displaystyle m}$和${\textstyle \sum _{v}{\binom {\deg(v)}{2}}}$。
• ${\displaystyle \chi _{E}(G)=\chi _{V}(L(G))}$，即原圖的邊色數等於線圖的點色數。
• ${\displaystyle G}$中的一個匹配對應了${\displaystyle L(G)}$中的一個獨立集，且其大小相等。於是，${\displaystyle G}$中最大匹配的大小等於${\displaystyle L(G)}$最大獨立集的大小。藉助這一關係，可以通過求解後者來求解前者，但反之不總是可行，因為並非所有圖都能表示為某個${\displaystyle G}$的線圖。在計算機科學中，最大匹配問題和最大獨立集問題是兩個重要的問題。前者已經被高效解決（Edmonds' Blossom Algorithm）；而後者則是NP完全問題，被普遍認為無法高效求解。
• 若${\displaystyle G}$存在歐拉迴路，則${\displaystyle L(G)}$存在哈密頓迴路，但反之不然。

惠特尼同構定理

惠特尼同構定理^[1]闡述了以下事實：設有連通圖${\displaystyle G_{1}}$和${\displaystyle G_{2}}$且它們均不是三角形${\displaystyle K_{3}}$或爪形${\displaystyle K_{1,3}}$。如果${\displaystyle L(G_{1})\cong L(G_{2})}$，那麼${\displaystyle G_{1}\cong G_{2}}$。也就是說，除了極特殊的情形，圖${\displaystyle G}$的結構可以由線圖${\displaystyle L(G)}$的結構中唯一地恢復出來。

其它性質

任何的線圖都是無爪的，亦即不包含${\displaystyle K_{1,3}}$作為導出子圖。因此，任意含有偶數個頂點的連通線圖都存在完美匹配。

線圖${\displaystyle L(G)}$的鄰接矩陣${\displaystyle A_{m\times m}}$的全部特徵值都不小於-2。這是因為${\displaystyle A=J^{\operatorname {T} }J-2I}$，其中${\displaystyle J_{n\times m}}$是原圖${\displaystyle G}$的關聯矩陣（incidence matrix）。又由於矩陣${\displaystyle J^{\operatorname {T} }J}$是半正定的，所以${\displaystyle A}$的任何特徵值${\displaystyle \lambda }$均滿足${\displaystyle \lambda +2\geq 0}$。

等價刻畫

九種排除在線圖之外的導出子圖

Beineke給出了線圖的一種等價刻畫：${\displaystyle H}$是某圖的線圖若且唯若${\displaystyle H}$不包含九種類型的導出子圖（見右圖）。^[2]

如果${\displaystyle H}$的最小度至少為5，那麼只有左邊一列和右邊一列是必要的。換言之，此時，${\displaystyle H}$是某圖的線圖若且唯若${\displaystyle H}$不包含六種類型的導出子圖（見右圖的左邊一列和右邊一列）。

參考文獻

1. Whitney, Hassler. Congruent Graphs and the Connectivity of Graphs. American Journal of Mathematics. 1932-01, 54 (1): 150 [2020-10-23]. doi:10.2307/2371086. （原始內容存檔於2020-10-26）.
2. Beineke, Lowell W. Characterizations of derived graphs. Journal of Combinatorial Theory. 1970-09-01, 9 (2): 129–135 [2020-10-23]. ISSN 0021-9800. doi:10.1016/S0021-9800(70)80019-9. （原始內容存檔於2020-10-30） （英語）.