Loading AI tools
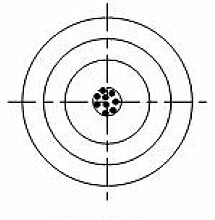
在測量學中,測量精度(measuring accuracy)[1][2]或精準度,是衡量測量結果的真實性與可靠性的指標,通常包含精密度[3](precision,或譯精確度)、準確度(accuracy)、正確度(trueness)及公差(tolerance)等含義。
此條目需要精通或熟悉相關主題的編者參與及協助編輯。 |
上述中,「準確度」被認為是由正確度和精密度組合而成,用于衡量觀測結果與其真值之間的接近程度;「正確度」指測量值的數學期望值與真實值之間的接近程度,反映了測量過程中系統誤差的大小;「精確度」指測量值與其數學期望值之間的離散程度,反映了測量過程中偶然誤差的大小。因此,準確度反映了偶然誤差和系統誤差的聯合影響[4]。
在中文語境下,「精度」常被用於指精密度或是精確度,「準度」則通常指準確度或是正確度的簡稱,「精準度」則是兩者複合的含糊用語。精度和準度的具體含意應根據語境進行判別,規範性文件則通常會迴避對「精度」的使用以免造成歧義[5][6]。

在1994年國際標準化組織發佈的關於測量精度概念的規範文件ISO 5725及其所對應的中華人民共和國國家標準GB/T 6379-2004 《測量方法與結果的準確度(正確度與精密度)》中,對測量精度的描述被分為準確度、正確度和精密度三個概念。該規範性文件的第一部分給出了對這三個概念的定義:
- 準確度(英語:accuracy):測試結果與接受參照值間的一致程度
- 正確度(英語:trueness):由大量測試結果得到的平均數與接受參照值間的一致程度
- 精密度(英語:precision):在規定條件下,獨立測試結果間的一致程度
與之相關的還有偏倚、重複性、再現性的概念:
- 偏倚(英語:bias):測試結果的期望值與接受參照值之差
- 重複性(英語:repeatability):在重複性條件下的精密度
- 再現性(英語:reproducibility):在再現性條件下的精密度
另外,對於準確度,ISO 5725註明「當用於一組測試結果時,由隨機誤差分量和系統誤差即偏倚分量組成」;對於重複性的註明是「正確度的度量通常用術語偏倚表示」以及「準確度曾被稱為『平均數的準確度』,這種用法不被推薦」;對於精密度的註明則是「精密度僅僅依賴於隨機誤差的分佈而與真值或規定值無關」「 精密度的度量通常以不精密度表達,其量值用測試結果的標準差來表示,精密度越低,標準差越大」。[7][8]
除GB/T 6379-2004以外,中華人民共和國國家計量技術規範JJF 1001-2001 《通用計量術語及定義》中亦以相近的描述定義準確度、正確度和精密度。[9]
中國大陸使用的測繪學領域規範性文件GB/T 14911-2008 《測繪基本術語》中僅定義了「準確度」與「精密度」:[10]
- 準確度(英語:accuracy):在一定測量條件下,對某一次的多次測量中,測量值的估值與其真值的偏離程度
- 精密度(英語:precision):在一定測量條件下,對某一次的多次測量中,各測量值間的離散程度
可見,測繪學中的「精密度」與ISO 5725及GB/T 6379-2004的概念相近,但前者的「準確度」則更接近於後者「正確度」的概念。而對於後者的「準確度」,測繪學有使用「精確度」一詞來代稱的情況。[4]另外,測繪學中的「精度指標」通常是指平均誤差、中誤差、極限誤差與相對誤差等衡量精密度的指標。[11][12]在不存在系統誤差時,測繪學中的「精確度」即可由「精度(精密度)」代稱;而存在系統誤差時,測繪學中的「精確度」則應由「精度(精密度)」和「準確度(正確度)」共同衡量。[5]

假設某一觀測量的真實值為 ,對其進行 次觀測,可以得到由 個觀測值組成的觀測向量
這些觀測量的測量誤差 是其真實值與觀測值之差:
以概率論中的中心極限定理為依據,測量誤差通常被視作是數學期望值為 ,標準差為 的隨機變量,並且服從於相應的正態分佈:
基於這一假設,可以採用統計學的方法構造各類指標對測量誤差的分佈情況進行分析,以評價測量結果的準確度、精密度和正確度。又由於偶然誤差和系統誤差具有不同的統計特性,即偶然誤差的數學期望值為零,但系統誤差不然。因此在進行測量結果的分析時,也常會將偶然誤差與系統誤差分別分析,即選用不同的精度指標來評價精密度和正確度。
偶然誤差是指在大小和符號上表現出偶然性,但總體上符合一定統計規律的誤差,其數學期望值為零。精密度即是對偶然誤差統計的描述。
其估計值由下列公式計算
通過方差是中誤差的平方的關係,亦可得到偶然誤差的方差及其估計值。
對於正態分佈,誤差分佈於與平均值距離一倍及二倍、三倍中誤差之間的概率分別為
在遠離平均值時,誤差出現的概率相當接近於零,可以在假設檢定中將其排除,而選定的排除「該誤差是偶然誤差」這一假設的極限值即為極限誤差。在測量學中,常以二倍或三倍中誤差作為極限誤差。
平均誤差即平均絕對誤差,對於一定觀測條件下的某組獨立的偶然誤差來說,是其絕對值的數學期望值:[4][13][14]
相應的估計值為
根據正態分佈的概率分佈函數,可以得出平均誤差 與中誤差 之間的數學關係:
即有
或然誤差 是使區間 內的累積概率分佈為 的值,即:[4][15]
且可解得
觀測量 中存在的系統誤差是指觀測量的真實值 與其數學期望值 之間的差值:
將其進行分解,可以得出以方差和系統誤差的平方和表示的均方誤差:
因此,均方誤差被認為同時包含了對偶然誤差和系統誤差的定量描述,可以衡量測量學中的「精確度」。
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.








![{\displaystyle \operatorname {E} [\Delta ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/87021a5a34b6680ab936ace389240bd911291dcc)

![{\displaystyle f(\Delta )={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {(\Delta -\operatorname {E} [\Delta ])^{2}}{2\sigma ^{2}}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b9aeee476f4c8750cad89de61d956fe415a2b2a0)
![{\displaystyle \operatorname {E} [\Delta ]=0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0bd4cf249d29da246e967f6bb5ca71db9e093b2d)
![{\displaystyle \sigma ={\sqrt {\operatorname {E} [\Delta ^{2}]-\operatorname {E} [\Delta ]^{2}}}={\sqrt {\operatorname {E} [\Delta ^{2}]}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/509ef858a73d84a1d6c92ebbd82e7ef4966bb3a5)


![{\displaystyle \theta =\operatorname {E} [\left\vert \Delta \right\vert ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0606b0b41e5cd7c23dfaa99bbe85aafe3f1b12d9)










![{\displaystyle \operatorname {E} [X]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/44dd294aa33c0865f58e2b1bdaf44ebe911dbf93)
![{\displaystyle \varepsilon ={\tilde {X}}-\operatorname {E} [X]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/97db5c06596218e19eb8ef594877b41e82f400d8)
![{\displaystyle \operatorname {MSE} [X]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/8865403232144105d39824cdf9ccae31ca8b8837)
![{\displaystyle \operatorname {MSE} [X]=\operatorname {E} [(X-{\tilde {X}})^{2}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/88b2eeca9c247a704c07ca19c81379f458997dd2)
![{\displaystyle {\begin{aligned}\operatorname {MSE} [X]&=\operatorname {E} [(X-{\tilde {X}})^{2}]\\[4pt]&=\operatorname {E} [[(X-\operatorname {E} [X])+(\operatorname {E} [X]-{\tilde {X}})]^{2}]\\[4pt]&=\operatorname {E} [(X-\operatorname {E} [X])^{2}+2(X-\operatorname {E} [X])(\operatorname {E} [X]-{\tilde {X}})+(\operatorname {E} [X]-{\tilde {X}})^{2}]\\[4pt]&=\operatorname {E} [(X-\operatorname {E} [X])^{2}]+2\operatorname {E} [(X-\operatorname {E} [X])(\operatorname {E} [X]-{\tilde {X}})]+\operatorname {E} [(\operatorname {E} [X]-{\tilde {X}})^{2}]\\[4pt]&=\sigma _{X}^{2}+2(\operatorname {E} [X]-\operatorname {E} [X])(\operatorname {E} [X]-{\tilde {X}})+\varepsilon ^{2}\\[4pt]&=\sigma _{X}^{2}+\varepsilon ^{2}\\[4pt]\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1c1c02b8f4fbe9586267f22ab5b2e63c048702b3)