德拜模型是普朗克黑體輻射定律的固體版本,後者把電磁輻射視為盒中的光子氣體,而德拜模型把原子的振動視為盒中的聲子(盒子就是這塊固體)。它們大部分的計算步驟都是相同的,因為聲子氣和光子氣都是有線性色散關係的玻色氣體。
考慮一個邊長為 的立方體。從盒中粒子一文可知,盒中的(沿某一邊長方向傳播的)聲波由於共振效應,其波長只能為:
的立方體。從盒中粒子一文可知,盒中的(沿某一邊長方向傳播的)聲波由於共振效應,其波長只能為:

其中 是整數。一個聲子的能量是:
是整數。一個聲子的能量是:

其中 是普朗克常數,
是普朗克常數, 是聲子的頻率。近似認為頻率與波長成反比,則有:
是聲子的頻率。近似認為頻率與波長成反比,則有:

其中 是固體中的聲速。推廣到三維的情況(沿任意方向傳播的聲子):
是固體中的聲速。推廣到三維的情況(沿任意方向傳播的聲子):

其中 為聲子的動量。頻率與波長成反比的近似(即聲速恆定)對於低能量聲子是準確的,但對於高能量聲子則不然(參見聲子)。這是德拜模型的局限之一,導致其對中間溫度的預言不正確,而對低溫和高溫都很精確。
為聲子的動量。頻率與波長成反比的近似(即聲速恆定)對於低能量聲子是準確的,但對於高能量聲子則不然(參見聲子)。這是德拜模型的局限之一,導致其對中間溫度的預言不正確,而對低溫和高溫都很精確。
下面來計算盒中的總能量:

其中 是盒中能量為
是盒中能量為 的聲子的數目。換句話說,總能量等於某能量的聲子數目乘以其能量再對各能量求和。在三維空間中,我們有:
的聲子的數目。換句話說,總能量等於某能量的聲子數目乘以其能量再對各能量求和。在三維空間中,我們有:

這是德拜模型和普朗克黑體輻射定律的不同之處。與盒中的電磁輻射不一樣,由於聲子不能有無限大的頻率,所以盒中聲子只有有限個能量狀態。它的頻率由它的傳播介質——固體的原子晶格所約束。考慮以下的橫向聲子的插圖:
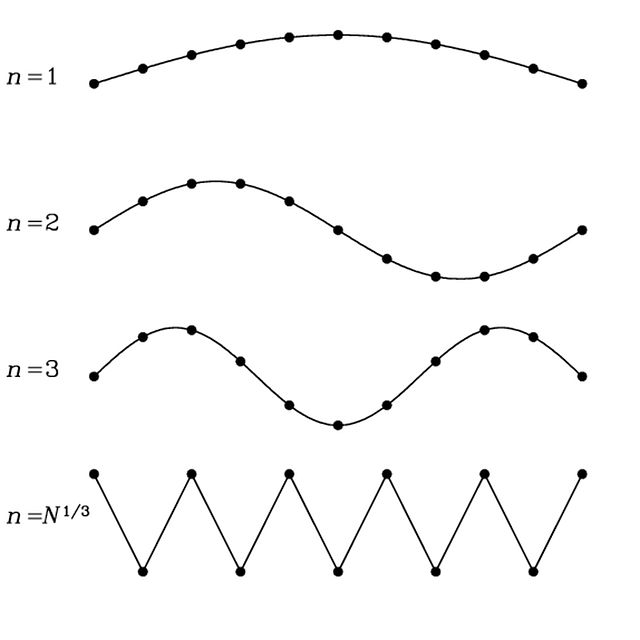
可以合理假設聲子的最小波長是原子間距的兩倍,如最下一圖所示。固體中有 個原子,我們的固體是正方體,因此每一條邊有
個原子,我們的固體是正方體,因此每一條邊有![{\displaystyle {\sqrt[{3}]{N}}}](//wikimedia.org/api/rest_v1/media/math/render/svg/2632439311fdaac0db5c94be22a66bc4759c3b3e) 個原子,原子間距為
個原子,原子間距為![{\displaystyle L/{\sqrt[{3}]{N}}}](//wikimedia.org/api/rest_v1/media/math/render/svg/68ce3128288fa487eb59b377703ca3c31b6ac01d) ,從而最小波長為:
,從而最小波長為:
![{\displaystyle \lambda _{\rm {min}}={2L \over {\sqrt[{3}]{N}}}\,,}](//wikimedia.org/api/rest_v1/media/math/render/svg/67ce39568ba1619356396b79fafe20ab2a5b958f)
最大的模數 (對於光子是無限大)為:
(對於光子是無限大)為:
![{\displaystyle n_{\rm {max}}={\sqrt[{3}]{N}}\,.}](//wikimedia.org/api/rest_v1/media/math/render/svg/52e26b34255058c420ca488f519532157f051097)
這設置了三重能量求和的上限:
![{\displaystyle U=\sum _{n_{x}}^{\sqrt[{3}]{N}}\sum _{n_{y}}^{\sqrt[{3}]{N}}\sum _{n_{z}}^{\sqrt[{3}]{N}}E_{n}\,{\bar {N}}(E_{n})\,.}](//wikimedia.org/api/rest_v1/media/math/render/svg/fec6d96639ee52ea7d4e59bc75e719fe094fd5ce)
對於緩慢變化的、表現良好的函數,求和可以用積分來代替(又稱為托馬斯-費米近似):
![{\displaystyle U\approx \int _{0}^{\sqrt[{3}]{N}}\int _{0}^{\sqrt[{3}]{N}}\int _{0}^{\sqrt[{3}]{N}}E(n)\,{\bar {N}}\left(E(n)\right)\,dn_{x}\,dn_{y}\,dn_{z}\,.}](//wikimedia.org/api/rest_v1/media/math/render/svg/4f378b750c04cde69b47b010798779902e74825b)
至此,我們還沒有提到 :能量為
:能量為 的聲子的數目。聲子服從玻色-愛因斯坦統計。它們的分佈由著名的玻色-愛因斯坦公式給出:
的聲子的數目。聲子服從玻色-愛因斯坦統計。它們的分佈由著名的玻色-愛因斯坦公式給出:

由於一個聲子有三個可能的偏振態(一個縱向、兩個橫向,大致攜帶相同的能量),需把以上公式乘以3:

實際上我們可以定義等效聲速 ,也就是說,德拜溫度
,也就是說,德拜溫度 (見下文)與
(見下文)與 成正比。更加精確地講,
成正比。更加精確地講, ,其中我們區分了縱向和橫向的聲波速度(貢獻分別為1/3和2/3)。德拜溫度或有效聲速是晶體的硬度的一種衡量。
,其中我們區分了縱向和橫向的聲波速度(貢獻分別為1/3和2/3)。德拜溫度或有效聲速是晶體的硬度的一種衡量。
把此式代入能量積分,得:
![{\displaystyle U=\int _{0}^{\sqrt[{3}]{N}}\int _{0}^{\sqrt[{3}]{N}}\int _{0}^{\sqrt[{3}]{N}}E(n)\,{3 \over e^{E(n)/kT}-1}\,dn_{x}\,dn_{y}\,dn_{z}\,.}](//wikimedia.org/api/rest_v1/media/math/render/svg/2b05660b876347cc0556fce9c94b050d78867006)
這比光子的情況容易得多,因為(在半經典式的處理中)光子的頻率(也即這個三重積分)是無上界的。但如上面圖所示,這一點對於聲子不成立。為了近似計算這個三重積分,德拜使用了球坐標系:

並用八分之一球(球在一個卦限內的部分)來近似代替立方體:

其中 是球的半徑,通過保持立方體和八分之一球中的粒子數目相同來得出。立方體的體積是
是球的半徑,通過保持立方體和八分之一球中的粒子數目相同來得出。立方體的體積是 :
:

因此:
![{\displaystyle R={\sqrt[{3}]{6N \over \pi }}\,.}](//wikimedia.org/api/rest_v1/media/math/render/svg/3f9d4e2bc889e4df97cb5eb25a732323e6d7dbd1)
用球的積分來代替立方體積分這一近似是德拜模型不準確性的另一來源。
先積分掉角向部分:

再利用變量代換 :
:

為簡化表達式,可以定義德拜溫度 ——它的因次與溫度相同,因物質而異:
——它的因次與溫度相同,因物質而異:
![{\displaystyle T_{D}\ {\stackrel {\mathrm {def} }{=}}\ {hc_{s}R \over 2Lk}={hc_{s} \over 2Lk}{\sqrt[{3}]{6N \over \pi }}={hc_{s} \over 2k}{\sqrt[{3}]{{6 \over \pi }{N \over V}}}}](//wikimedia.org/api/rest_v1/media/math/render/svg/411d5aa9ab5603b7ea4354a1a15d081145b5d11d)
於是比內能為:

其中 是(第三)德拜函數。
是(第三)德拜函數。
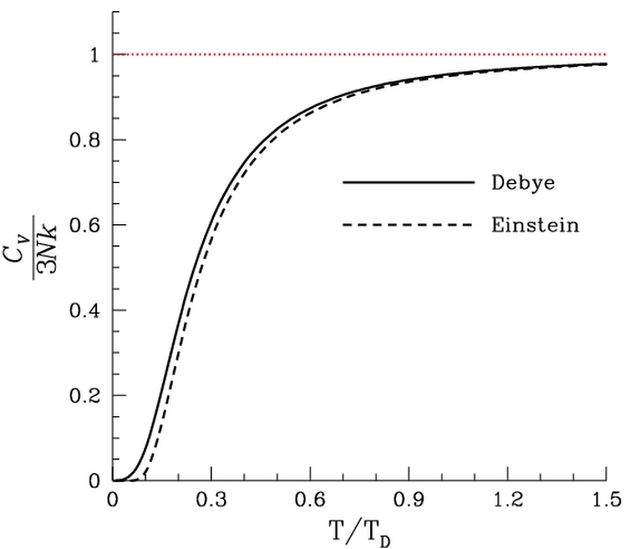
對 微分,我們便得到無因次熱容:
微分,我們便得到無因次熱容:

這個公式給出了任何溫度下德拜模型的結果。下面更簡單的公式給出了低溫和高溫極限下的漸近表現。前面已經提到,這兩個漸進表現是精確的,而中間溫度的表現則不然。其根本原因在於,低溫和高溫近似下,德拜模型都給出了其一,低頻下精確的色散關係 ,其二,精確的狀態密度(單位頻率間隔內的聲子數目)
,其二,精確的狀態密度(單位頻率間隔內的聲子數目) 。
。



















![{\displaystyle {\sqrt[{3}]{N}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2632439311fdaac0db5c94be22a66bc4759c3b3e)
![{\displaystyle L/{\sqrt[{3}]{N}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/68ce3128288fa487eb59b377703ca3c31b6ac01d)
![{\displaystyle \lambda _{\rm {min}}={2L \over {\sqrt[{3}]{N}}}\,,}](http://wikimedia.org/api/rest_v1/media/math/render/svg/67ce39568ba1619356396b79fafe20ab2a5b958f)
![{\displaystyle n_{\rm {max}}={\sqrt[{3}]{N}}\,.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/52e26b34255058c420ca488f519532157f051097)
![{\displaystyle U=\sum _{n_{x}}^{\sqrt[{3}]{N}}\sum _{n_{y}}^{\sqrt[{3}]{N}}\sum _{n_{z}}^{\sqrt[{3}]{N}}E_{n}\,{\bar {N}}(E_{n})\,.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/fec6d96639ee52ea7d4e59bc75e719fe094fd5ce)
![{\displaystyle U\approx \int _{0}^{\sqrt[{3}]{N}}\int _{0}^{\sqrt[{3}]{N}}\int _{0}^{\sqrt[{3}]{N}}E(n)\,{\bar {N}}\left(E(n)\right)\,dn_{x}\,dn_{y}\,dn_{z}\,.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4f378b750c04cde69b47b010798779902e74825b)








![{\displaystyle U=\int _{0}^{\sqrt[{3}]{N}}\int _{0}^{\sqrt[{3}]{N}}\int _{0}^{\sqrt[{3}]{N}}E(n)\,{3 \over e^{E(n)/kT}-1}\,dn_{x}\,dn_{y}\,dn_{z}\,.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2b05660b876347cc0556fce9c94b050d78867006)




![{\displaystyle R={\sqrt[{3}]{6N \over \pi }}\,.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3f9d4e2bc889e4df97cb5eb25a732323e6d7dbd1)




![{\displaystyle T_{D}\ {\stackrel {\mathrm {def} }{=}}\ {hc_{s}R \over 2Lk}={hc_{s} \over 2Lk}{\sqrt[{3}]{6N \over \pi }}={hc_{s} \over 2k}{\sqrt[{3}]{{6 \over \pi }{N \over V}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/411d5aa9ab5603b7ea4354a1a15d081145b5d11d)


























