布拉菲晶格

在幾何學以及晶體學中，布拉菲晶格（又譯布拉菲點陣）(Bravais lattices)是為了紀念法國物理學家奧古斯特·布拉菲 (Auguste Bravais （1850）),^[1]而命名的，布拉菲晶格是由一組離散平移操作生成的無限離散點陣列，在三維空間中的描述為

${\displaystyle \mathbf {R} =n_{1}\mathbf {a} _{1}+n_{2}\mathbf {a} _{2}+n_{3}\mathbf {a} _{3},}$

7種晶系及其三維布拉菲晶格

其中n_i為任意整數，a_i為原始平移向量或原始向量，它們位於不同的方向（不一定相互垂直），並跨越網格。對於給定的布拉菲晶格，原始向量的選擇並不是唯一的。任何布拉菲晶格的一個基本特徵是，對於任何方向的選擇，當從所選方向觀察時，從每個離散晶格點所看到的晶格都是完全相同的。

布拉菲晶格概念用於正式定義晶體排列及其（有限）邊界。晶體由每個晶格點上的一個或多個原子（稱為基點或母題motif）組成。晶基可能由原子、分子或固體物質的聚合物串組成，晶格提供了晶基的位置。

如果兩個布拉菲晶格具有同構空間對稱群，則通常認為它們是等價的。 從這個意義上講，在2維空間中存在5種可能的布拉菲晶格，在3維空間中存在14種可能的布拉菲晶格。 布拉菲晶格的14個可能的對稱群是230個空間群中的14個。 在空間群分類的背景下，布拉菲晶格也稱為"布拉菲類"、"布拉菲算術類"或"布拉菲聚類"(Bravais flocks)^[2]。

在3維空間

鑽石立方晶格的 2×2×2 單元格

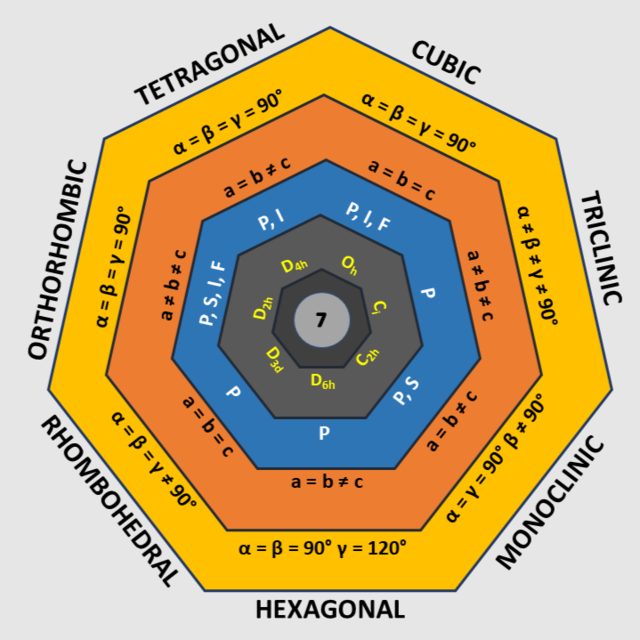
三維布拉菲晶格只有14種可能。這14種布拉菲晶格可分成7種晶系，每種晶系又可依中心原子在晶胞中的位置不同再分成6種晶格：

• 簡單（P）：晶格點只在晶格的八個頂點處
• 體心（I）：除八個頂點處有晶格點外，晶胞中心還有一個晶格點
• 面心（F）：除八個頂點處有晶格點外，在六個面的中央還有一個晶格點
• 底心（A，B或C）：除八個頂點處有晶格點外，在晶胞的一組平行面（A，B或C）的每個面中央還有一個晶格點

7種不同晶系與每種晶系的6種不同晶格共有7 × 6 = 42種組合，但是有些組合其實是相同的，都能組成14種布拉菲晶格。例如，單斜晶系的體心晶格可以通過單斜晶系的底心（C）晶格選擇不同的晶軸得到，所以這兩種其實是同一種；同樣，所有的底心（A）、底心（B）晶格都相當於底心（C）或簡單（P）晶格。因此，去除相同的組合，可以得到14種不同的布拉菲晶格，列於下表（晶格圖下方是代表該布拉菲晶格的皮爾遜符號，表中空白的格表示於已有的晶格重複）：

晶系	點陣常數特徵	14種布拉菲晶格
		簡單（P）	底心（C）	體心（I）	面心（F）
三斜晶系	a≠b≠c，α≠β≠γ≠90°
單斜晶系	a≠b≠c，α=γ=90°≠β
斜方晶系 （正交晶系）	a≠b≠c，α=β=γ=90°
四方晶系	a=b≠c，α=β=γ=90°
三方晶系 （棱方晶系）	a=b=c，α=β=γ≠90°
六方晶系	a=b≠c，α=β=90º，γ=120°
等軸晶系 （立方晶系）	a=b=c，α=β=γ=90°

每一個單位晶格的體積可以由${\displaystyle \mathbf {a} \cdot \mathbf {b} \times \mathbf {c} }$計算得知。其中${\displaystyle \mathbf {a} ,\mathbf {b} }$,和${\displaystyle \mathbf {c} }$是晶格向量。各種布拉菲晶格的體積如下：

晶系	體積
三斜晶系	${\displaystyle abc{\sqrt {1-\cos ^{2}\alpha -\cos ^{2}\beta -\cos ^{2}\gamma +2\cos \alpha \cos \beta \cos \gamma }}}$
單斜晶系	${\displaystyle abc\sin \alpha }$
斜方晶系	${\displaystyle abc}$
四方晶系	${\displaystyle a^{2}c}$
三方晶系	${\displaystyle a^{3}{\sqrt {1-3\cos ^{2}\alpha +2\cos ^{3}\alpha }}}$
六方晶系	${\displaystyle {\frac {{\sqrt {3\,}}\,a^{2}c}{2}}}$
等軸晶系	${\displaystyle a^{3}}$

在4維空間

在四維空間中，共有64個布拉菲晶格。其中，23個是簡單晶格 (primitive) ，41個是中心晶格 (centered)。有10個布拉菲晶格分成"對映體對"(enantiomorphic pair)。^[3]

參見

• 晶體慣態
• 晶系
• translational symmetry
• lattice (group)
• classification of lattices
• 密勒指數
• 威廉·勞倫斯·布拉格
• X射線晶體學
• 奧古斯特·布拉菲

參考文獻

1. Aroyo, Mois I.; Müller, Ulrich; Wondratschek, Hans. Historical Introduction. International Tables for Crystallography. 2006, A1 (1.1): 2–5 [2008-04-21]. CiteSeerX 10.1.1.471.4170 . doi:10.1107/97809553602060000537. （原始內容存檔於2013-07-04）.
2. Bravais class. Online Dictionary of Crystallography. IUCr. [8 August 2019]. （原始內容存檔於2008-05-13）.
3. Brown, Harold; Bülow, Rolf; Neubüser, Joachim; Wondratschek, Hans; Zassenhaus, Hans, Crystallographic groups of four-dimensional space, New York: Wiley-Interscience [John Wiley & Sons], 1978, ISBN 978-0-471-03095-9, MR 0484179

外部連結

• Contemporary Bravis Lattice Structures^{[永久失效連結]} Designed by Tom Barber
• Catalogue of Lattices (by Nebe and Sloane)
• Smith, Walter Fox. The Bravais Lattices Song. 2002.