哈密頓圖

漢米頓圖（中國大陸作哈密頓圖，台灣作漢米頓圖）又稱漢密頓圖，是指存在哈密頓環的無向圖，由哈密頓爵士提出。

十二面體中的哈密頓迴路

定義

下列定義，既適用於無向圖，亦適用於有向圖。

哈密頓路徑

圖的一條路，經過每個頂點恰好一次。

哈密頓環

在一條哈密頓路的基礎上，再有一條邊將其首尾連接，所構成的圈。注意，若有一個哈密頓圈，則移除其任一條邊，皆可得到一條哈密頓路，但反之則不然，即給定一條哈密頓路，不一定能延伸成哈密頓圈，因為該路徑的首尾兩頂點之間，不一定有邊相連。

哈密頓圖

有哈密頓圈的圖。

半哈密頓圖

有哈密頓路，但無哈密頓圈的圖。

哈密頓連通圖

一幅圖，以其任意兩個頂點為起終點，皆存在一條哈密頓路。

哈密頓分解

將邊集分劃成若干個哈密頓圈。

亞哈密頓圖

亞哈密頓圖（英語：Hypohamiltonian graph）並非哈密頓圖，但只要移除任何一個頂點，就會變成哈密頓圖。

• 
  非哈密頓圖
• 
  半哈密頓圖
• 
  哈密頓圖

性質

哈密爾頓圖的必要條件： 若G=(V,E) 是一個哈密爾頓圖，則對於V的每一個非空子集S，均有W(G－S) ≤|S|。其中|S|是S中的頂點數，W(G－S)表示圖G擦去屬於S中的頂點後，剩下子圖的連通分支的個數。

充分條件

對歐拉圖而言，有某個充要條件，可用作簡單判定一幅圖是否歐拉圖（歐拉定理）。然而，對於哈密頓圖，並無相應的結果。

不過，仍有一系列越來越鬆的判別條件，能夠斷定一幅圖必定為哈密頓圖。^[1]此類定理，最早見於蓋布瑞·狄拉克（英語：Gabriel Andrew Dirac）1952年的研究，其想法直觀，即只要有「足夠多」邊，就能迫得圖有哈密頓圈。用頂點的度推出存在哈密頓圈的定理之中，目前最優的，是1976年邦迪與赫瓦塔爾的定理。

以上是有關無向圖的部分。對於有向圖，相應的定理舉例有Ghouila–Houiri。

狄拉克定理

蓋布瑞·狄拉克（英語：Gabriel Andrew Dirac）於1952年^[2]證明以下定理：^[3]

${\displaystyle n}$個頂點的簡單圖（${\displaystyle n\geq 3}$）中，若每個頂點的度皆至少為${\displaystyle {\frac {n}{2}}}$，則必為哈密頓圖。

歐爾定理

主條目：奧爾定理

設 ${\displaystyle G=(V,E)}$ 是一個無向簡單圖，${\displaystyle |V|=n}$，${\displaystyle n\geq 3}$。若對於任意兩個不相鄰的頂點 ${\displaystyle u,v\in V}$，都有 ${\displaystyle u}$ 和 ${\displaystyle v}$ 的度，即 ${\displaystyle d(u)}$ 與 ${\displaystyle d(v)}$ 滿足 ${\displaystyle d(u)+d(v)\geq n}$，那麼，${\displaystyle G}$ 是哈密爾頓圖。

此條件由挪威圖論數學家奧斯丁·歐爾在1960年給出。

波紹定理

波紹·拉約什（英語：Lajos Pósa (mathematician)）證明了幾條有關哈密頓圈的定理。以下具體引用一條1962年的定理^[4][5]，有關連邊少的頂點：

一幅${\displaystyle n}$個頂點的完全圖（${\displaystyle n\geq 3}$），若滿足：

1. 對所有滿足${\displaystyle 1\leq k<{\frac {n-1}{2}}}$的整數${\displaystyle k}$，度不大於${\displaystyle k}$的頂點個數，嚴格小於${\displaystyle k}$；
2. 度不大於${\displaystyle {\frac {n-1}{2}}}$的頂點個數，小於或等於${\displaystyle {\frac {n-1}{2}}}$；

則必為哈密頓圖。

注意${\displaystyle n}$為偶時，條件2已包含於條件1，所以只在${\displaystyle n}$為奇數時，條件2才需要分開列出。

應用波紹定理的例子

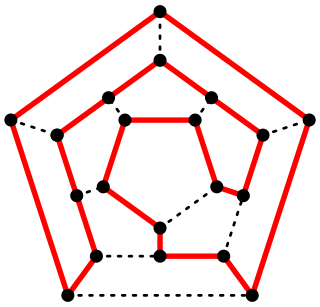
作為例子，考慮附圖中，具有${\displaystyle 6}$個頂點的圖。其為哈密頓圖：已經將頂點排列好，使哈密頓圈${\displaystyle H}$（以紅色標示）正好是外圈。

• 狄拉克定理不足以證明該圖為哈密頓圖。若要應用狄拉克定理，則所有頂點的度皆要至少為${\displaystyle 3}$，然而圖中有頂點的度僅為${\displaystyle 2}$。
• 奧爾定理同樣不敷使用，因為圖中標出的兩個不相鄰頂點${\displaystyle a,b}$的度，和僅為${\displaystyle d(a)+d(b)=3+2=5}$，但奧爾定理的條件中，至少要有${\displaystyle 6}$。
• 另一方面，波紹定理能夠斷定該圖必為哈密頓圖，因為只有${\displaystyle 0}$個度為${\displaystyle 1}$的頂點，以及${\displaystyle 1}$個度為${\displaystyle 2}$的頂點，故已滿足條件1（因為${\displaystyle 0<1}$且${\displaystyle 0+1<2}$）。

例子

赫歇爾圖（英語：Herschel graph）

• 超過2個頂點的完全圖是哈密頓圖。${\displaystyle n}$階無向完全圖${\displaystyle K_{n}}$上，不同的（無向）哈密頓圈有${\displaystyle {\frac {(n-1)!}{2}}}$個。而若考慮方向，則有${\displaystyle (n-1)!}$個有向哈密頓圈。
• ${\displaystyle n}$個頂點的圖當中，最少邊數的哈密頓圖是循環圖${\displaystyle C_{n}}$。任何循環圖皆為哈密頓圖。
• 循環賽圖（英語：Tournament (graph theory)）有奇數條（有向）哈密頓路徑。任意（多於兩個頂點的）循環賽圖為哈密頓圖當且僅當其為強連通。^[6]
• 任何以柏拉圖立體（凸正多面體）的邊與頂點構成的圖（「1-骨架（英語：n-skeleton）」）皆為哈密頓圖。^[7][8]
• 同樣，稜柱與反稜柱的1-骨架也是哈密頓圖。
• 13種阿基米德立體的1-骨架皆為哈密頓圖，但13種卡塔蘭立體當中，僅有7個的1-骨架是哈密頓圖。^[9][10].
• 赫歇爾圖（英語：Herschel graph）（附圖）是眾多不具哈密頓圈的凸多面體1-骨架當中，最小的一個。^[11]
• 哈密頓圖的線圖仍是哈密頓圖。^[12]:408
• 歐拉圖的線圖也是哈密頓圖。

哈密頓路徑問題

主條目：哈密頓路徑問題

尋找哈密頓路徑是一個典型的NP-完全問題。後來人們也證明了，找一條哈密頓路的近似比為常數的近似算法也是NP-完全的。

尋找哈密頓路的確定算法雖然很難有多項式時間的，但是這並不意味着只能進行時間複雜度為${\displaystyle O(n\times n!)}$暴力搜索。利用狀態壓縮動態規劃^{[來源請求]}，可以將時間複雜度降低到${\displaystyle O(2^{n}\cdot n^{3})}$，具體算法是建立方程f[i][S][j]，表示經過了i個節點，節點都是集合S的，到達節點j時的最短路徑。每次都按照點j所連的節點進行轉移。

參見

• 哈密頓路徑
• 哈密頓路徑問題

參考文獻

1. Melissa DeLeon. Department of Mathematics and Computer Science, Seton Hall University , 編. A Study of Sufficient Conditions for Hamiltonian Cycles (PDF). [2021-09-19]. （原始內容存檔 (PDF)於2012-12-22） （英語）.
2. Dirac, Gabriel Andrew. Some theorems on abstract graphs. Proc. London Math. Soc. 3. 1952, 2: 6––81. MR 0047308. doi:10.1112/plms/s3-2.1.69 （英語）.
3. Ronald Graham. Handbook of Combinatorics. MIT Press. 1995. ISBN 978-0-262-57170-8 （英語）.
4. Pósa, Lajos. A theorem concerning hamilton lines. Magyar Tud. Akad. Mat. Kutató ́Int. Közl. 1962, 7: 225–226 （英語）.
5. Nash-Williams, Crispin. On Hamiltonian circuits in finite graphs (PDF). Proc. Amer. Math. Soc. 1966, 17: 466–467 [2021-09-19]. （原始內容存檔 (PDF)於2022-02-17） （英語）.
6. Graham 1995，第29 & 31頁 harvnb模板錯誤: 無指向目標: CITEREFGraham1995 (幫助).
7. Gardner, M. "Mathematical Games: About the Remarkable Similarity between the Icosian Game and the Towers of Hanoi." Sci. Amer. 196, 150–156, May 1957. [2021-09-03]. （原始內容存檔於2016-10-22）.
8. Weisstein, Eric W. (編). Wolfram MathWorld (首頁). at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英語）.
9. Weisstein, Eric W. (編). Wolfram MathWorld (首頁). at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英語）.
10. Weisstein, Eric W. (編). Wolfram MathWorld (首頁). at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英語）.
11. Weisstein, Eric W. (編). Wolfram MathWorld (首頁). at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英語）.
12. Xiong, Liming; Liu, Zhanhong. Hamiltonian iterated line graphs [哈密頓的疊代線圖]. Discrete Mathematics. 2002, 256: 407–422. doi:10.1016/S0012-365X(01)00442-3 （英語）.