包絡

物理學和工程學中，震盪信號的包絡是一條勾勒出極值的光滑曲線。^[1]因此，包絡將恆定振幅的概念推廣為瞬時振幅。下圖展示了在上包絡與下包絡之間振盪的調製正弦曲線。包絡函數可以是時間、空間、角度或任何變量的函數。

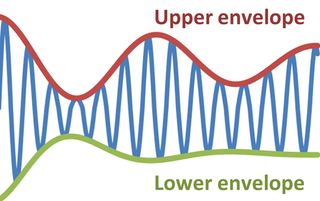調製正弦曲線的包絡

拍頻波

由兩個振幅相同、波長和頻率幾乎相同的正弦波相加產生的調製波。

在空間x和時間t中產生包絡函數的常見情況是波長和頻率幾乎相同的兩個波的疊加：^[2]

${\displaystyle {\begin{aligned}F(x,\ t)&=\sin \left[2\pi \left({\frac {x}{\lambda -\Delta \lambda }}-(f+\Delta f)t\right)\right]+\sin \left[2\pi \left({\frac {x}{\lambda +\Delta \lambda }}-(f-\Delta f)t\right)\right]\\[6pt]&\approx 2\cos \left[2\pi \left({\frac {x}{\lambda _{\rm {mod}}}}-\Delta f\ t\right)\right]\ \sin \left[2\pi \left({\frac {x}{\lambda }}-f\ t\right)\right]\end{aligned}}}$

其中使用了兩個正弦波相加的三角函數，以及近似值Δλ ≪ λ：

${\displaystyle {\frac {1}{\lambda \pm \Delta \lambda }}={\frac {1}{\lambda }}\ {\frac {1}{1\pm \Delta \lambda /\lambda }}\approx {\frac {1}{\lambda }}\mp {\frac {\Delta \lambda }{\lambda ^{2}}}.}$

此處調製波長λ_mod來自下式：^[2][3]

${\displaystyle \lambda _{\rm {mod}}={\frac {\lambda ^{2}}{\Delta \lambda }}\ .}$

調製波長是包絡波長的兩倍，因為餘弦波的每半個波長都控制着正弦波的正負值。同樣，拍頻是包絡波的頻率，是調製波頻率的兩倍，即2Δf。^[4]

如果這種波是聲波，耳朵聽到的是與f有關的頻率，振幅隨拍頻的變化而變化。^[4]

相速度與群速度

紅色方塊以相速度移動，綠色圓圈以群速度傳播。

除2π之外，上述正弦波的參數是：

${\displaystyle \xi _{C}=\left({\frac {x}{\lambda }}-f\ t\right)\ ,}$

${\displaystyle \xi _{E}=\left({\frac {x}{\lambda _{\rm {mod}}}}-\Delta f\ t\right)\ ,}$

下標C、E分別指載波和包絡。同樣的振幅F來自相同的ξ_C、ξ_E值，在適當相關的x、t選擇下，每個本身都可能返回到相同的值。這種不變性意味着可以在空間中追蹤波形，並找到固定振幅的位置在時間中傳播時的速度；要使載波參數保持不變，條件為：

${\displaystyle \left({\frac {x}{\lambda }}-f\ t\right)=\left({\frac {x+\Delta x}{\lambda }}-f(t+\Delta t)\right)\ ,}$

這表明，要保持恆定振幅，距離Δx與時間間隔Δt的關係是相速度 v_p

${\displaystyle v_{\rm {p}}={\frac {\Delta x}{\Delta t}}=\lambda f\ .}$

另一方面，同樣的考慮表明包絡線是群速度 v_g:^[5]

${\displaystyle v_{\rm {g}}={\frac {\Delta x}{\Delta t}}=\lambda _{\rm {mod}}\Delta f=\lambda ^{2}{\frac {\Delta f}{\Delta \lambda }}\ .}$

引入波向量k，可得更常見的群速度表達式：

${\displaystyle k={\frac {2\pi }{\lambda }}\ .}$

注意到，對於微小變化Δλ而言，相應的波向量小變化Δk為：

${\displaystyle \Delta k=\left|{\frac {dk}{d\lambda }}\right|\Delta \lambda =2\pi {\frac {\Delta \lambda }{\lambda ^{2}}}\ ,}$

於是群速度可重寫為：

${\displaystyle v_{\rm {g}}={\frac {2\pi \Delta f}{\Delta k}}={\frac {\Delta \omega }{\Delta k}}\ ,}$

其中ω是以弧度/秒為單位的頻率：ω = 2πf。在所有介質中，頻率和波向量都與色散關係ω = ω(k)有關，群速度可以寫成：

${\displaystyle v_{\rm {g}}={\frac {d\omega (k)}{dk}}\ .}$

與GaAs晶格振動對應的某些波的色散關係ω=ω(k)。^[6]

在經典真空等介質中，電磁波的色散關係為：

${\displaystyle \omega =c_{0}k}$

其中c₀是經典真空中的光速。這種情況下，相速度和群速度都是c₀。

在所謂色散介質中，色散關係可能是波向量的複雜函數，相速度和群速度也不盡相同。例如，對於GaAs中原子振動（聲子）表現出的幾種波，不同波向量k方向的色散關係如圖所示。一般而言，相速度和群速度的方向可能不同。^[7]

函數近似

參見：K·p微擾論

根據包絡函數計算的GaAs-GaAlAs異質結中160Ǻ GaAs量子阱最低兩個量子態的電子概率。^[8]

凝聚態物理學中，晶體中移動電荷載流子的能量本徵函數可表為布洛赫波：

${\displaystyle \psi _{n\mathbf {k} }(\mathbf {r} )=e^{i\mathbf {k} \cdot \mathbf {r} }u_{n\mathbf {k} }(\mathbf {r} )\ ,}$

其中n是帶的編號（如導帶或價帶），r是空間位置，k是波矢。指數是正弦變化函數，對應一個緩慢變化的包絡，調製波函數u_{n, k}的快速變化部分，描述波函數在晶格原子核心附近的行為。包絡只限於晶體布里淵區限定範圍內的k值，這就限制了它隨位置r變化的速度。

用量子力學確定載流子行為時，通常使用包絡近似法。其中薛定諤方程被簡化到僅指包絡的行為，邊界條件直接應用於包絡函數，而非完整的波函數。^[9]例如，被困在雜質附近的載流子波函數受包絡函數F支配，函數是布洛赫函數的疊加：

${\displaystyle \psi (\mathbf {r} )=\sum _{\mathbf {k} }F(\mathbf {k} )e^{i\mathbf {k\cdot r} }u_{\mathbf {k} }(\mathbf {r} )\ ,}$

其中包括F(k)的傅立葉分量由近似薛定諤方程求得。^[10]在某些應用中，周期部分u_k被帶緣附近的值取代，如k=k₀，接着：^[9]

${\displaystyle \psi (\mathbf {r} )\approx \left(\sum _{\mathbf {k} }F(\mathbf {k} )e^{i\mathbf {k\cdot r} }\right)u_{\mathbf {k} =\mathbf {k} _{0}}(\mathbf {r} )=F(\mathbf {r} )u_{\mathbf {k} =\mathbf {k} _{0}}(\mathbf {r} )\ .}$

繞射圖樣

雙峰繞射圖樣具有單縫包絡線。

多縫繞射圖樣的包絡由單縫繞射圖樣決定，後者的包絡線如下：^[11]

${\displaystyle I_{1}=I_{0}\sin ^{2}\left({\frac {\pi d\sin \alpha }{\lambda }}\right)/\left({\frac {\pi d\sin \alpha }{\lambda }}\right)^{2}\ ,}$

其中α是繞射角，d是狹縫寬度，λ是波長。對多個狹縫，圖樣為^[11]

${\displaystyle I_{q}=I_{1}\sin ^{2}\left({\frac {q\pi g\sin \alpha }{\lambda }}\right)/\sin ^{2}\left({\frac {\pi g\sin \alpha }{\lambda }}\right)\ ,}$

其中q為狹縫數量，g是光柵常數。第一個因子即單縫結果I₁，調製着第二個變化更快的因子，取決於狹縫數量與間距。

估計

包絡檢波器是從信號中提取包絡的電子電路。

在數碼訊號處理中，可用希爾伯特變換或滑動平均RMS振幅估計包絡。^[12]

另見

• 解析信號#復包絡/基帶

• 包絡線
• 包絡追蹤
• 瞬時頻率
• 調變
• 振動 (數學)

參考文獻

1. C. Richard Johnson, Jr; William A. Sethares; Andrew G. Klein. Figure C.1: The envelope of a function outlines its extremes in a smooth manner. Software Receiver Design: Build Your Own Digital Communication System in Five Easy Steps. Cambridge University Press. 2011: 417. ISBN 978-0521189446.
2. Blair Kinsman. Wind Waves: Their Generation and Propagation on the Ocean Surface Reprint of Prentice-Hall 1965. Courier Dover Publications. 2002: 186. ISBN 0486495116.
3. Mark W. Denny. Air and Water: The Biology and Physics of Life's Media. Princeton University Press. 1993: 289. ISBN 0691025185. 含有內容需登入查看的頁面 (link)
4. Paul Allen Tipler; Gene Mosca. Physics for Scientists and Engineers, Volume 1 6th. Macmillan. 2008: 538. ISBN 978-1429201247.
5. Peter W. Milonni; Joseph H. Eberly. §8.3 Group velocity. Laser Physics 2nd. John Wiley & Sons. 2010: 336. ISBN 978-0470387719.
6. Peter Y. Yu; Manuel Cardona. Fig. 3.2: Phonon dispersion curves in GaAs along high-symmetry axes. Fundamentals of Semiconductors: Physics and Materials Properties 4th. Springer. 2010: 111. ISBN 978-3642007095.
7. V. Cerveny; Vlastislav Červený. §2.2.9 Relation between the phase and group velocity vectors. Seismic Ray Theory. Cambridge University Press. 2005: 35. ISBN 0521018226.
8. G Bastard; JA Brum; R Ferreira. Figure 10 in Electronic States in Semiconductor Heterostructures. Henry Ehrenreich; David Turnbull (編). Solid state physics: Semiconductor Heterostructures and Nanostructures. 1991: 259. ISBN 0126077444.
9. Christian Schüller. §2.4.1 Envelope function approximation (EFA). Inelastic Light Scattering of Semiconductor Nanostructures: Fundamentals And Recent Advances. Springer. 2006: 22. ISBN 3540365257.
10. For example, see Marco Fanciulli. §1.1 Envelope function approximation. Electron Spin Resonance and Related Phenomena in Low-Dimensional Structures. Springer. 2009: 224 ff. ISBN 978-3540793649.
11. Kordt Griepenkerl. Intensity distribution for diffraction by a slit and Intensity pattern for diffraction by a grating. John W Harris; Walter Benenson; Horst Stöcker; Holger Lutz (編). Handbook of physics. Springer. 2002: 306 ff. ISBN 0387952691.
12. Envelope Extraction - MATLAB & Simulink. MathWorks. 2021-09-02 [2021-11-16]. （原始內容存檔於2023-10-19）.