位能

位能（potential energy，中國大陸譯勢能^{[註 1]}，港台譯位能）是儲存於一物理系統內的一種能量，是一個用來描述物體在保守力場中作功能力大小的物理量。保守力作功與路徑無關，故可定義一個僅與位置有關的函數，使得保守力沿任意路徑所作的功，可表達為這兩點函數值的差，這個函數便是位能。

古代攻城用的重力拋石機，利用平衡重鎚的重力位能，將石頭拋向敵城。

亞洲最大的天荒坪抽水蓄能電站將電力用位能的形式儲存

從物理意義上來說，位能表示物體在特定位置上所儲存的能量，描述作功能力的大小。在適當的情況下，位能可以轉化為例如動能、內能等其他能量。

位能

位能的保守力定義

主條目：保守力

如果分別作用於兩個質點上的作用力與反作用力作功與具體路徑無關，只取決於相互作用質點初末位置，那麼這樣的一對力就叫作保守力。不滿足這個條件的則稱為非保守力。可以證明保守場的幾個等價條件^[2]，於是我們得到保守力的性質有：

1. 保守力沿給定兩點間作功與路徑無關；
2. 保守力沿任意環路作功為零；
3. 保守力可以表示為一個純量函數的（負）梯度；

推廣到多質點體系和連續分佈物體，如果一封閉系統中任意兩個質點之間的作用力都是保守力，則稱該系統為保守體系。保守體系的位形，即在保守體系中各質點的相對位置發生變化時，其間的相互作用力作功，作功之和只與各質點相對位置有關。將保守體系在保守力作用下的這種與相對位置相聯繫的作功的能力定義為一個函數，稱為該保守體系的勢能函數或位能函數，簡稱勢能或位能^[3]。這樣，體系從一種位形變為另一種位形時對外界所作的功等於後者與前者的位能之差，從而賦予了位能函數以直觀的物理意義。

除此之外，我們還可以將位能的定義從現在的基礎上拓展。比如熱學中氣體分子間的相互作用位能，它是大量分子位能的和，實際不是用相對位置（位形）來描述的，而是用體積、溫度、壓強等熱學參量。又如，在一些特定的約束條件下，某些平時是非保守力的力也成為了保守力^[4]，或者幾種力的淨力恰巧成為了一個保守力。

廣義位能

主條目：廣義位能

對於一個理想、完整體系，有拉格朗日方程式

${\displaystyle {\frac {\mbox{d}}{{\mbox{d}}t}}{\frac {\partial T}{\partial {\dot {q}}_{\alpha }}}-{\frac {\partial T}{\partial q_{\alpha }}}=Q_{\alpha }\qquad \alpha =1,2,\cdots ,s}$

其中，T為體系動能，q_α為廣義坐標的α分量，Q_α為廣義力淨力的α分量，s為廣義坐標數。在傳統的位能定義下，保守力淨力可以寫為

${\displaystyle F_{i}=-{\frac {\partial V}{\partial x_{i}}}\qquad i=1,2,3}$

其中，V為體系位能。用廣義坐標寫為

${\displaystyle Q_{\alpha }=-{\frac {\partial V}{\partial q_{\alpha }}}\qquad \alpha =1,2,\cdots ,s}$

代入拉格朗日方程式便可得到

${\displaystyle {\frac {\mbox{d}}{{\mbox{d}}t}}{\frac {\partial (T-V)}{\partial {\dot {q}}_{\alpha }}}-{\frac {\partial (T-V)}{\partial q_{\alpha }}}=0\qquad \alpha =1,2,\cdots ,s}$

若廣義力Q_α並不能表示成關於任意函數V的上述函數，卻能找到另一個函數U，使得Q_α可以表示為

${\displaystyle Q_{\alpha }=-{\frac {\partial U}{\partial q_{\alpha }}}+{\frac {\mbox{d}}{{\mbox{d}}t}}{\frac {\partial U}{\partial {\dot {q}}_{\alpha }}}\qquad \alpha =1,2,\cdots ,s}$

則代入拉格朗日方程式仍有

${\displaystyle {\frac {\mbox{d}}{{\mbox{d}}t}}{\frac {\partial (T-U)}{\partial {\dot {q}}_{\alpha }}}-{\frac {\partial (T-U)}{\partial q_{\alpha }}}=0\qquad \alpha =1,2,\cdots ,s}$

這時U具有與V相似的數學形式，但已經不再與保守力有關。我們把U叫做廣義位能^[5]。

廣義位能最主要的應用在於帶電粒子在電磁場中的運動上。帶有電荷q，以速度v移動的粒子在電場E和磁場B中受到勞侖茲力

${\displaystyle {\boldsymbol {F}}=q({\boldsymbol {E}}+{\boldsymbol {v}}\times {\boldsymbol {B}})}$

再輔以麥克斯韋方程組，定義電勢φ與向量勢A，可以得到一個滿足上述條件的函數^[6]

${\displaystyle U=q(\phi -{\boldsymbol {A}}\cdot {\boldsymbol {v}})}$

在下面的介紹中，不經特殊說明，我們只涉及傳統意義上的位能，不涉及廣義位能。

性質

位能為能量的一種，具有能量因次，在國際單位制下的單位是焦耳（J），另外在涉及到粒子物理時常用到電子伏特（eV），高斯單位制下為爾格（erg）。位能一般使用「E_p」^[3]表示，也常使用「W」^[7]「U」和「V」^[8]。

位能是一個純量函數，當一個物體與多個物體共有位能或共有多種位能時，這個物體所具有的總位能為所有位能的代數和。

由定義可知，位能取決於兩個或多個物體的相對位形，是兩個或多個物體所共有的。然而，在兩物體A、B組成的保守體系中，如果我們以其中一個物體A作為參考系，則位能僅取決於另一物體B的相對位置。這時，在不引起混淆的情況下，我們常把「A、B具有的位能」稱作是「B的位能」。比如，在電場中的電荷具有靜電勢能，或者是在一個天體附近的另一個天體具有重力位能。除此之外，有時候保守體系中只存在一個物體，位能來自於物體內部各部分間的相對位移，這時候我們也說，位能是這個物體所具有的。比如，彈簧，或者是具有體分佈電荷的絕緣體球。

需要注意的是，即使在同一保守力場中的同一處，不同物體的位能也一般不同，比如在重力作用範圍內，物體的重力位能不僅取決於其高度，還取決於其質量。

物理意義

三峽水力發電站。用大壩將水高高蓄起，然後在大壩處飛瀉而下，帶動發電機。雖然經過一系列複雜的轉換，然而電能的根本來源是水的重力位能。

當物體從高位能處來到低位能處時，該物體位能減少，而保守力向外作等量功使其它某種能量增加。從中我們可以發現，位能可以表示一個物體所儲存的能量的多少。如，放在高處的物體相比放在放在低處的物體而言具有更多的重力位能，當它從空中向下墜落的時候，重力位能減少，轉化為動能；而當它沿粗糙斜面下滑時，重力位能同時轉化為動能和內能。

具有更多位能的物體有能力對外界作出更多的功。^[9]故，當物體在保守力的作用下從a處沿任意路徑移動到b處時，位能變化量為保守力作功的相反值，即

${\displaystyle E_{p}(b)-E_{p}(a)=-W_{a\to b}=-\int _{a}^{b}{\boldsymbol {F}}_{con}\cdot {\mbox{d}}{\boldsymbol {r}}}$

通常我們並不在意位能的絕對大小，而是關心其變化量，這從位能的定義可以明顯看出；實際上，談一個物體究竟擁有多少絕對位能是沒有意義的。不過，有時為了計算或者敘述方便，我們也取一個位能零點O，規定O處位能E_p(O)=0，這樣質點在a點的位能大小為

${\displaystyle E_{p}(a)=-W_{O\to a}=-\int _{O}^{a}{\boldsymbol {F}}_{con}\cdot {\mbox{d}}{\boldsymbol {r}}}$

原則上位能零點可任意取，一般依方便而定；如果可能，一般選F_con=0點為位能零點。^[10]

位能為保守力關於位移的積分，相對地，保守力為相應位能函數關於位移的負梯度，即

${\displaystyle {\boldsymbol {F}}_{con}=-\nabla E_{p}}$

使用廣義坐標描述時，可寫為

${\displaystyle E_{p}(b)-E_{p}(a)=-W_{a\to b}=-\sum _{\alpha =1}^{s}\int _{a}^{b}Q_{\alpha }{\mbox{d}}q_{\alpha }}$

${\displaystyle Q_{\alpha }=-\sum _{\alpha =1}^{s}{\frac {\partial E_{p}}{\partial q_{\alpha }}}}$

描述位能隨位置變化的圖稱為位能圖。若位能為僅與一個坐標（或廣義坐標）有關的函數，這時位能圖成為位能曲線，可以在平面直角坐標系上表示出來，這時負梯度退化為負導數，

${\displaystyle F_{con}=-{\frac {\partial E_{p}}{\partial x}}}$

在下面介紹平衡及各種位能的時候會有位能曲線的範例。

機械能

主條目：機械能

位能E_p與動能E_k之和稱為機械能。

${\displaystyle E=E_{k}+E_{p}}$

外力的功與非保守內力的功之和等於質點系機械能的增量，這就是質點系的功能原理。用數學方式表達出來為

${\displaystyle W_{ex}+W_{nci}=E(b)-E(a)}$

在x方向上運動的一個機械能守恆的粒子，遭遇到勢阱與勢壘

其中，${\displaystyle W_{ex}}$為外力作功，${\displaystyle W_{nci}}$為非保守內力作功。若${\displaystyle W_{ex}=0}$，${\displaystyle W_{nci}=0}$，則質點系機械能守恆，這就是機械能守恆定律。這時，質點系與外界無能量交換，內部也無機械能與非機械能的轉化，只有動能與位能的相互轉換。

在構建理想模型時，機械能守恆定律應用得十分廣泛，特別是當一質點處在連心力場時，其機械能守恆；又因為動能E_k>0，在已知總能量的情況下，可以了解到質點理論上的行動範圍（滿足E_k<E的區域）。

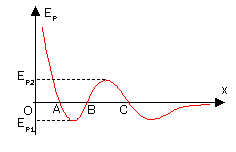
設在x方向上有如圖位能曲線，則我們把AB間位能最低處叫作勢阱（C右方也有一個勢阱），BC間位能最高處叫作勢壘，對應的有勢阱深度與勢壘高度。我們設定粒子機械能守恆，那麼：

假設一個粒子從無窮遠處靠近，其機械能為E=0，那麼在C點處其動能為零，再向左走動能為負，速度將為虛數，經典力學中這是不允許的。因此它最多只能到達C處。隨着粒子機械能（即初動能）的增大，其運動範圍的左端將會延伸，當其機械能達到或超過E_p2時，它將可以翻過勢壘。

再假設一個粒子，初始時在AB間。若它機械能為0，那麼它可以在AB間運動，其最大動能為E_{k max}=E_p1。當其機械能不斷增大，達到E_p2時，它將可以翻越勢壘，到達B右方空間（當然，其在A左方的空間也會延伸）。

粒子在A點不穩定平衡，在B點穩定平衡，在C點隨遇平衡。

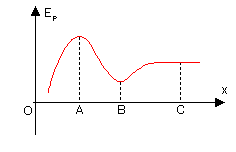
位能圖、勢壘等概念是討論單個質點在保守外場中運動的有力工具，在物理學多個領域中的應用都十分廣泛。^[11]

物體在位能場中的平衡

只受保守力作用的物體，總有向總位能更低處運動的趨勢。當物體所處位置不受力作用或淨力為零時，即${\displaystyle {\frac {\partial E_{p}}{\partial x}}=0}$，則稱物體處於平衡。右圖A、B、C三點皆處於平衡。

當物體偏離平衡位置時，若受淨力背向平衡位置，則物體有離開平衡位置的趨勢，則稱物體處於不穩定平衡。位能曲線上，不穩定平衡即滿足${\displaystyle {\frac {\partial ^{2}E_{p}}{\partial x^{2}}}<0}$的點。右圖A點處於不穩定平衡。

當物體偏離平衡位置時，若受淨力指向平衡位置，則物體有回到平衡位置的趨勢，則稱物體處於穩定平衡。位能曲線上，穩定平衡即滿足${\displaystyle {\frac {\partial ^{2}E_{p}}{\partial x^{2}}}>0}$的點。右圖B點處於穩定平衡。

馬鞍面，即雙曲拋物面。從馬鞍面原點出發，在x方向上為穩定平衡，在y方向上為不穩定平衡。

當物體在平衡位置附近時淨力恆為零，則稱物體處於隨遇平衡。位能曲線上，隨遇平衡即滿足${\displaystyle {\frac {\partial ^{2}E_{p}}{\partial x^{2}}}=0}$的點。右圖C點處於隨遇平衡。

以上只是一種粗略的分析方法，實際上，在二維或高維空間中情況會更加複雜，比如，在不同的方向上具有不同的平衡種類^[12]。一個最簡單的例子是，若物體被約束在馬鞍形位能曲面上，位於中心時，在x方向上為穩定平衡，在y方向上為不穩定平衡。

勢

主條目：位勢

在物理中有時會提到勢，請不要與位能相混淆。勢通常表述為位能與一個物理量的比值，如電勢（一個粒子靜電勢能與其電荷量的比值），重力勢（一個物體重力位能與其質量的比值）。一個確定保守力場中，一個物體的位能與該物體有關，但勢的分佈與該物體無關^[13]。

需要與位能區分開的是，物體並不一定總是向勢更低的地方運動。一個正電荷會趨向於達到電勢更低的地方，但一個負電荷會趨向於達到電勢更高的地方，但那裏都分別是它們位能更低處。

勢也包括一些位能所不包括的內容，如磁向量勢。

幾種常見位能

下面介紹幾種常見位能。

在下面的介紹中，我們常考慮一個兩質點組成的保守體系，兩質點間受且僅受相應的一種保守力。兩質點的位能是一種最簡單、最理想的模型，然而也是實際模型的基礎。實際的問題理論上都可以由兩質點位能的函數加以積分得到。

引力位能

引力和引力位能隨r變化的示意圖

主條目：萬有引力

• 注意：在臺灣將萬有引力統稱為「重力」，然而在大陸地區將萬有引力稱作「引力」，而將「重力」作為萬有引力的一種特殊簡化情形。這裏為了分別介紹兩種情況，不致混淆，暫採用大陸命名方法。

根據牛頓萬有引力定律，對於兩質點m₀、m，質點m受到的萬有引力為

${\displaystyle {\boldsymbol {F}}({\boldsymbol {r}})=-Gmm_{0}{\cfrac {{\boldsymbol {r}}-{\boldsymbol {r_{0}}}}{|{\boldsymbol {r}}-{\boldsymbol {r_{0}}}|^{3}}}}$

其中G是萬有引力常數，m₀、m是兩質點的質量，r₀、r分別為兩質點的位置向量。重力場中的物體會具有重力位能。對於兩個質點，定義無窮遠處為位能零點，則質點m在r處的引力位能為

${\displaystyle E_{G}({\boldsymbol {r}})=-Gmm_{0}{\frac {1}{|{\boldsymbol {r}}-{\boldsymbol {r_{0}}}|}}}$

在實際問題中，對於已知重力勢分佈φ=φ(r)，質點m在r處的重力位能為

${\displaystyle E_{G}({\boldsymbol {r}})=m\phi ({\boldsymbol {r}})}$

重力位能

主條目：萬有引力 § 重力的量與單位

重力和重力位能隨h變化的示意圖

重力位能是引力位能在一種特殊情況下的簡化形式。可以證明^[14]，對一球對稱分佈物體在其外一質點產生的引力，上面兩質點間的作用力公式仍適用，其中m₀為該物體總質量，r₀為其球心位矢。當 |r-r₀| 在不太大範圍內變動時，對作用力公式取零級近似，作用力不變，則引力退化為重力。^[15]由此可見，重力的近似要求很嚴格。然而由於在日常生活中這個條件很容易滿足，而且極簡便，符合人們的日常生活經驗，故仍有研究價值，單列一項。

在這種情況下，重力大致^[16]只與星體性質與物體質量有關，而與位置無關，方向鉛直向下^[17]。將重力加速度定為常數g，則物體重力大小為

${\displaystyle F(h)=mg}$

其中m為物體質量，g為重力加速度常數。則物體在h處的重力位能為

${\displaystyle E_{p}(h)=mgh}$。

其中h為物體的高度。

重力位能並沒有嚴格的位能零點定義，完全依計算方便而定，不過比較常用的是以地面或桌面為位能零點。

在地球上g的值約為9.8 ms^-2，在不同地區稍有不同。這個值已經包括了和地球自轉所需的向心力造成的差別。一般計算中g可近似的取作標準重力加速度，即g=g_n=9.80665 ms^{-2 [18]}。

彈性位能

彈簧的彈力和彈性位能隨x變化的示意圖

主條目：虎克定律

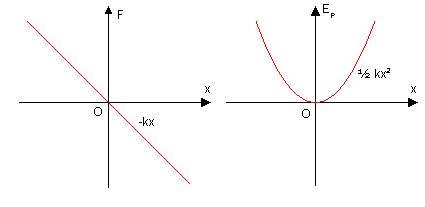
彈簧、鋼片、金屬絲等滿足虎克定律的物體，在彈性限度內應力與應變成正比。下面以彈簧為例。在彈性限度內，彈簧彈力與長度變化量的關係為

${\displaystyle {\boldsymbol {F}}({\boldsymbol {x}})=kx}$

其中，k為彈簧彈性係數，x為彈簧長度變化（即固定一端時另一端相對平衡位置的位移）。則其彈性位能為

${\displaystyle E_{p}(x)={\frac {1}{2}}kx^{2}}$

彈性位能為對應物體自身所擁有，一般選擇彈簧原長時（x=0）為位能零點。

電勢能

主條目：電勢能

一個質子受到的另一個質子的靜電力和電勢能隨r變化的示意圖

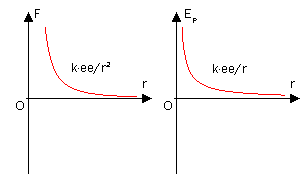
在靜電學裏，根據庫倫定律，對於兩靜止點電荷q、q₀，點電荷q受到的靜電力為

${\displaystyle {\boldsymbol {F}}({\boldsymbol {r}})={\frac {qq_{0}}{4\pi \epsilon _{0}}}{\cfrac {{\boldsymbol {r}}-{\boldsymbol {r_{0}}}}{|{\boldsymbol {r}}-{\boldsymbol {r_{0}}}|^{3}}}}$

其中ε₀是電常數，r₀、r分別為兩點電荷的位置向量。靜電場中的點電荷會具有電勢能。對於兩個點電荷，定義無窮遠處為位能零點，則點電荷q在r處的電勢能為

${\displaystyle W({\boldsymbol {r}})={\frac {qq_{0}}{4\pi \epsilon _{0}}}{\frac {1}{|{\boldsymbol {r}}-{\boldsymbol {r_{0}}}|}}}$。

在實際問題中，對於已知電勢分佈φ=φ(r)，點電荷q在r處的電勢能為

${\displaystyle E_{G}({\boldsymbol {r}})=q\phi ({\boldsymbol {r}})}$

電勢能基於靜電場的定律庫侖定律。在變化電磁場中，粒子受力不再為保守力，不再能單獨用一個純量勢函數描述，需要使用純量勢φ與向量勢A共同描述^[19]。

分子位能

蘭納-瓊斯勢中，分子間作用力和分子位能隨r變化的示意圖

分子力實際上來源於多個方面，精確的計算與各分子內部結構有很大關係，會變得十分複雜。對於無極性分子，兩分子間作用力可近似用以下半經驗公式表示：^[20]

${\displaystyle F(r)={\frac {\lambda }{r^{s}}}-{\frac {\mu }{r^{t}}}}$

其中正表示排斥力，負表示牽引力；r為兩分子間距，λ、μ、s、t為常數，隨兩分子不同而不同，且s>t。這種力的特點是

• 在某一個值r₀以內，分子裏表現為排斥力並且隨r減小而急劇上升；
• 在r₀以外表現為牽引力，分子力逐漸增大，到某最大值後減小；
• 力程短，在r約為r₀十倍時已幾乎為零。

由此，對無極性分子間的相互作用位能有以下幾個常用曲線。一個典型且常用的模型是蘭納-瓊斯勢^[21]，該位能僅與兩分子間距有關，具有球對稱性，其函數解析式為

蘇則朗勢。

${\displaystyle E_{p}(r)=E_{p0}\left[\left({\frac {r_{0}}{r}}\right)^{12}-2\left({\frac {r_{0}}{r}}\right)^{6}\right]}$

其中，r為兩分子距離，E_p0為分子位能的勢阱（位能最低處的位能絕對值），r₀為勢阱處兩分子間距。E_p0與r₀需要對於具體分子通過實驗確定。

對蘭納-瓊斯勢在排斥力部分簡化，成為蘇則朗勢（Sutherland potential），即

${\displaystyle E_{p}(r)={\begin{cases}\infty &r\leq d\\-E\left({\frac {d}{r}}\right)^{6}&r>d\end{cases}}}$

其中E、d為常數，因分子而異。滿足蘇則朗勢的氣體稱為范德瓦爾斯氣體，分子力又稱作范德瓦爾斯力，滿足范德瓦爾斯方程式^[22]。

剛球勢。

對蘇則朗勢在重力部分再次簡化，成為剛球勢，即

${\displaystyle E_{p}(r)={\begin{cases}\infty &r\leq d\\0&r>d\end{cases}}}$

d=0時，分子位能完全忽略，變為質點勢，這時氣體稱作理想氣體^[23]，滿足理想氣體狀態方程式。

參見條目

• 能量
• 保守力
• 磁向量勢
• 拉格朗日方程式

註釋

1. 大氣科學中多稱「位能」^[1]。

參考文獻

1. 位能. 術語在線. 全國科學技術名詞審定委員會. （簡體中文）
2. 文麗，吳良大．《高等數學·第二冊：物理類（修訂版）》，P354。
3. 鄭永令，賈起民，方小敏．《力學（第二版）》，P157。
4. 見磁純量勢。
5. 以上證明見金尚年，馬永利．《理論力學（第二版）》，P48。
6. 金尚年，馬永利．《理論力學（第二版）》，P49。
7. 賈瑞皋，薛慶忠．《電磁學（第二版）》，P46。
8. 金尚年，馬永利．《理論力學（第二版）》，P18。
9. 用非保守力對物體作功可以增加物體的總位能，而若用保守力對物體作功，則物體一種位能增加而另一種位能減少，總位能不變。
10. 舒幼生．《力學（物理類）》，P86。
11. 趙凱華，羅蔚茵．《力學（第二版）》，P115。
12. 鄭永令，賈起民，方小敏．《力學（第二版）》，P163。
13. 準確地說，當該物體對周圍環境影響足夠小時。比如電場中一個電量很小的點電荷（被稱作試探電荷），當電量較大時會嚴重影響到周圍物體上的電荷分佈從而影響到勢分佈。關於試探電荷見電場#電場強度或賈起民，鄭永令，陳暨耀．《電磁學（第二版）》，P13。
14. 趙凱華，羅蔚茵．《力學（第二版）》，P337。
15. 實際對於重力的定義略稍複雜，參見萬有引力#兩者的微妙差別。
16. 對於計入離心力的重力定義，重力還與物體所處經緯度有關。參見萬有引力#兩者的微妙差別。另外，由於地球實際分佈非完全球對稱及地球實際略橢，也導致重力在各地有微小差異。
17. 由於離心力的原因，在一般情況下「鉛直向下」方向並不指向地心，然而重力方向仍然是與鉛直向下方向完全一致的。
18. 存档副本. [2010-01-12]. （原始內容存檔於2009-02-24）.
19. 使用拉格朗日方程式時也可以使用廣義位能U=q(φ+v·A)描述，見#廣義位能
20. 包科達．《熱物理學基礎》，P44。
21. 包科達．《熱物理學基礎》，P45。
22. 包科達．《熱物理學基礎》，P58。
23. 包科達．《熱物理學基礎》，P48。

延伸閱讀

• 舒幼生. 《力学（物理类）》. 北京: 北京大學出版社. 2005. ISBN 7-301-09401-9.

• 趙凱華，羅蔚茵. 《新概念物理教程·力学（第二版）》. 北京: 高等教育出版社. 2004. ISBN 7-04-015201-0.

• 文麗，吳良大. 《高等数学·第二册：物理类（修订版）》. 北京: 北京大學出版社. 2002. ISBN 7-301-07543-X.

• 鄭永令，賈起民，方小敏. 《力学（第二版）》. 北京: 高等教育出版社. 2002. ISBN 978-7-04-011084-5.

• 賈起民，鄭永令，陳暨耀. 《电磁学（第二版）》. 北京: 高等教育出版社. 2003. ISBN 7-04-008603-4.

• 金尚年，馬永利. 《理论力学（第二版）》. 北京: 高等教育出版社. 2002. ISBN 7-04-010808-9.

• 包科達. 《热物理学基础》. 北京: 高等教育出版社. 2001. ISBN 7-04-010154-8.