愛因斯坦模型

愛因斯坦模型是一種固體模型，基於三種假設：^[1]:131-132

• 晶格中的每一個原子都是三維量子諧振子；
• 原子不互相作用；
• 所有的原子都以相同的頻率振動（與德拜模型不同）。

阿爾伯特·愛因斯坦

第一個假設是相當準確的，而第二個假設則不是。如果原子真的不互相作用，那麼聲波就不會在固體內傳播。

歷史上的影響

原先的理論是由愛因斯坦在1907年提出的，具有很大的歷史相關性。由杜隆-泊替定律所預言的固體的熱容已經知道是與經典力學一致的。然而，低溫下的實驗觀察表明，熱容在絕對零度時趨於零，在高溫時單調增加到杜隆-泊替定律的預言。利用普朗克的量子化假設，愛因斯坦第一次能夠預言所觀察到的實驗趨勢。與光電效應在一起，這成為需要量子化的最重要的證據之一（值得注意的是，愛因斯坦是在現代量子力學的出現的許多年之前解決了量子諧振子問題）。儘管它成功了，但是愛因斯坦卻錯誤預言為指數趨近於零，而正確的表現則是遵守${\displaystyle T^{3}}$冪定律。這個缺陷後來由德拜模型在1912年糾正。^[2]:389ff

熱容（微正則系綜）

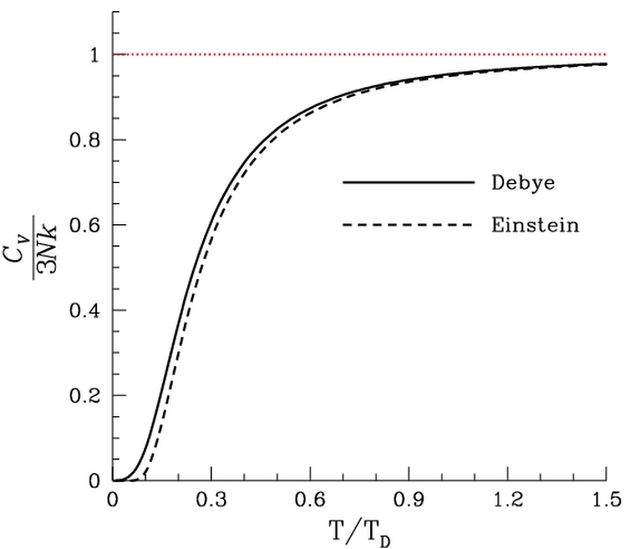
比較德拜、愛因斯坦分別對於熱容與溫度之間關係的預測。注意到在高溫時趨於3Nk的實驗值

恆定體積V的物體的熱容，通過內能U定義為：

${\displaystyle C_{V}=\left({\partial U \over \partial T}\right)_{V}.}$

${\displaystyle T}$是系統的溫度，可以從熵求出：

${\displaystyle {1 \over T}={\partial S \over \partial U}.}$

為了求出熵，考慮由${\displaystyle N}$個原子所組成的固體，每一個原子都有3個自由度。因此，總共有${\displaystyle 3N}$個量子諧振子（以下稱SHO）。

${\displaystyle N^{\prime }=3N}$

SHO的可能的能量為：

${\displaystyle E_{n}=\hbar \omega \left(n+{1 \over 2}\right)}$

或者說，能階是均勻分隔的，我們可以定義能量的量子：

${\displaystyle \varepsilon =\hbar \omega }$

它是SHO的能量可以增長的最小的，也是唯一的數量。接着，我們必須計算系統的多重性。也就是說，計算有多少種方法把${\displaystyle q}$個能量量子分佈在${\displaystyle N^{\prime }}$個SHO。我們可以想像把${\displaystyle q}$個石頭分佈在${\displaystyle N^{\prime }}$個盒子中：

或把一堆石頭分成${\displaystyle N^{\prime }-1}$份：

或把${\displaystyle q}$個石頭和${\displaystyle N^{\prime }-1}$個劃分排成一行：

最後一個圖最能說明問題。把${\displaystyle n}$ 樣東西排成一行，有${\displaystyle n!}$ 種方法。因此，把${\displaystyle q}$個石頭和${\displaystyle N^{\prime }-1}$個劃分排成一行的方法有${\displaystyle \left(q+N^{\prime }-1\right)!}$ 種，然而，如果把第2個劃分和第5個劃分互換位置，是沒有任何不同的。相同的理由對量子也成立。為了得出可能的不可區分的排列方法，我們必須把排列的總數除以不可區分的排列的數目。一共有${\displaystyle q!}$種相同的量子排列，以及${\displaystyle (N^{\prime }-1)!}$ 種相同的劃分排列。因此，系統的多重性為：

${\displaystyle \Omega ={\left(q+N^{\prime }-1\right)! \over q!(N^{\prime }-1)!}}$

正如上面所提及的，這就是把${\displaystyle q}$個能量量子放在${\displaystyle N^{\prime }-1}$個諧振子中的方法數目。系統的熵具有下列形式：

${\displaystyle S/k=\ln \Omega =\ln {\left(q+N^{\prime }-1\right)! \over q!(N^{\prime }-1)!}.}$

${\displaystyle N^{\prime }}$是一個很大的數，把它減去一總體上沒有任何影響：

${\displaystyle S/k\approx \ln {\left(q+N^{\prime }\right)! \over q!N^{\prime }!}}$

利用斯特靈公式的幫助，熵可以簡化：

${\displaystyle S/k\approx \left(q+N^{\prime }\right)\ln \left(q+N^{\prime }\right)-N^{\prime }\ln N^{\prime }-q\ln q.}$

固體的總能量為：

${\displaystyle U={N^{\prime }\varepsilon \over 2}+q\varepsilon .}$

我們現在來計算溫度：

${\displaystyle {1 \over T}={\partial S \over \partial U}={\partial S \over \partial q}{dq \over dU}={1 \over \varepsilon }{\partial S \over \partial q}={k \over \varepsilon }\ln \left(1+N^{\prime }/q\right)}$

把這個公式兩邊取倒數，以求出U：

${\displaystyle U={N^{\prime }\varepsilon \over 2}+{N^{\prime }\varepsilon \over e^{\varepsilon /kT}-1}.}$

兩邊關於溫度求導，以求出${\displaystyle C_{V}}$：

${\displaystyle C_{V}={\partial U \over \partial T}={N^{\prime }\varepsilon ^{2} \over kT^{2}}{e^{\varepsilon /kT} \over \left(e^{\varepsilon /kT}-1\right)^{2}}}$

或

${\displaystyle C_{V}=3Nk\left({\varepsilon \over kT}\right)^{2}{e^{\varepsilon /kT} \over \left(e^{\varepsilon /kT}-1\right)^{2}}}$

雖然固體的愛因斯坦模型準確預言高溫時的熱容，在低溫時與實驗值仍有明顯的差距。關於低溫時準確的熱容計算，參見德拜模型。

熱容（正則系綜）

熱容可以通過利用SHO的正則配分函數來獲得。

${\displaystyle Z=\sum _{n=0}^{\infty }e^{-E_{n}/kT}}$

其中

${\displaystyle E_{n}=\varepsilon \left(n+{1 \over 2}\right)}$

把該式代入配分函數的公式，得：

${\displaystyle {\begin{aligned}Z&{}=\sum _{n=0}^{\infty }e^{-\varepsilon \left(n+1/2\right)/kT}=e^{-\varepsilon /2kT}\sum _{n=0}^{\infty }e^{-n\varepsilon /kT}=e^{-\varepsilon /2kT}\sum _{n=0}^{\infty }\left(e^{-\varepsilon /kT}\right)^{n}\\&{}={e^{-\varepsilon /2kT} \over 1-e^{-\varepsilon /kT}}={1 \over e^{\varepsilon /2kT}-e^{-\varepsilon /2kT}}={1 \over 2\sinh \left({\varepsilon \over 2kT}\right)}.\end{aligned}}}$

這是一個SHO的配分函數。因為，統計上來說，固體的熱容、能量，以及熵，都是在它的原子（SHO）中均勻分佈的，因此我們可以利用這個配分函數來獲得這些物理量，然後直接把它們乘以${\displaystyle N^{\prime }}$以得出總量。接着，我們來計算每一個諧振子的平均能量：

${\displaystyle \langle E\rangle =u=-{1 \over Z}\partial _{\beta }Z}$

其中

${\displaystyle \beta ={1 \over kT}.}$

因此：

${\displaystyle u=-2\sinh \left({\varepsilon \over 2kT}\right){-\cosh \left({\varepsilon \over 2kT}\right) \over 2\sinh ^{2}\left({\varepsilon \over 2kT}\right)}{\varepsilon \over 2}={\varepsilon \over 2}\coth \left({\varepsilon \over 2kT}\right).}$

於是，一個諧振子的熱容為：

${\displaystyle C_{V}={\partial U \over \partial T}=-{\varepsilon \over 2}{1 \over \sinh ^{2}\left({\varepsilon \over 2kT}\right)}\left(-{\varepsilon \over 2kT^{2}}\right)=k\left({\varepsilon \over 2kT}\right)^{2}{1 \over \sinh ^{2}\left({\varepsilon \over 2kT}\right)}.}$

整個固體的熱容由${\displaystyle C_{V}=3NC_{V}}$給出：

${\displaystyle C_{V}=3Nk\left({\varepsilon \over 2kT}\right)^{2}{1 \over \sinh ^{2}\left({\varepsilon \over 2kT}\right)}.}$

它與前面推導的公式是相等的。

物理量${\displaystyle T_{E}=\varepsilon /k}$的因次是溫度，是晶體的一個特有的性質。它稱為「愛因斯坦溫度」。因此，愛因斯坦晶體模型預言晶體的能量和熱容是無因次比率${\displaystyle T/T_{E}}$的通用函數。類似地，德拜模型預言了比率${\displaystyle T/T_{D}}$的通用函數。