热门问题
时间线
聊天
视角
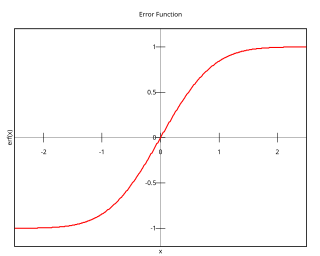
誤差函數
乙狀結構特殊函數,發生在概率,統計和偏微分方程中 来自维基百科,自由的百科全书
Remove ads
在數學中,誤差函數[註 1](英語:Error function)是一個特殊函數[註 2],符號。誤差函數在概率論,統計學以及偏微分方程中都有廣泛的應用。它的定義如下:[1][2]

Remove ads
分類
互補誤差函數,記為 erfc,在誤差函數的基礎上定義:
虛誤差函數,記為 erfi,定義為:
複誤差函數,記為w(z),也在誤差函數的基礎上定義:
Remove ads
詞源
誤差函數來自測度論,後來與測量誤差無關的其他領域也用到這一函數,但仍然使用誤差函數這一名字。
Remove ads
性質
誤差函數是奇函數:
對於任何 複數 z:
其中 表示 z的 複共軛。
複數平面上,函數 ƒ = exp(−z2) 和 ƒ = erf(z) 如圖所示。粗綠線表示 Im(ƒ) = 0,粗紅線表示 Im(ƒ) < 0, 粗藍線為 Im(ƒ) > 0。細綠線表示 Im(ƒ) = constant,細紅線表示 Re(ƒ) = constant<0,細藍線表示 Re(ƒ) = constant>0。
在實軸上, z → ∞時,erf(z) 趨於1,z → −∞時,erf(z) 趨於−1 。在虛軸上, erf(z) 趨於 ±i∞。
誤差函數是整函數,沒有奇異點(無窮遠處除外),泰勒展開收斂。
誤差函數泰勒級數:
對每個複數 z均成立。 上式可以用迭代形式表示:
誤差函數的導數:
誤差函數的 不定積分為:
Remove ads

逆誤差函數 可由 麥克勞林級數表示:
其中, c0 = 1 ,
即:
逆互補誤差函數定義為:
Remove ads
互補誤差函數的漸近展開,
其中 (2n – 1)!! 為 雙階乘,x為實數,該級數對有限 x發散。對於 ,有
其中餘項用以 大O符號表示為
- as .
餘項的精確形式為:
對於比較大的 x, 只需漸近展開中開始的幾項就可以得到 erfc(x)很好的近似值。[註 3]
Remove ads
互補誤差函數的連分式展開形式:[3]
Remove ads
初等函數近似表達式
- (最大誤差: 5·10−4)
其中, a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
- (最大誤差:2.5·10−5)
其中, p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
- (最大誤差: 3·10−7)
其中, a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
- (最大誤差: 1.5·10−7)
其中, p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
以上所有近似式適用範圍是: x ≥ 0. 對於負的 x, 誤差函數是奇函數這一性質得到誤差函數的值, erf(x) = −erf(−x).
另有近似式:
其中,
該近似式在0或無窮的鄰域非常準確,x整個定義域上,近似式最大誤差小於0.00035,取 a ≈ 0.147 ,最大誤差可減小到0.00012。[4]
逆誤差函數近似式:
Remove ads
數值近似
下式在整個定義域上,最大誤差可低至 :[5]
其中,
Remove ads
與其他函數的關係
誤差函數本質上與標準正態累積分佈函數是等價的,
可整理為如下形式:
的逆函數為正態分位函數,即概率單位函數,
誤差函數為標準正態分佈的尾概率Q函數的關係為,
誤差函數是米塔-列夫勒函數的特例,可以表示為合流超幾何函數,
為 符號函數.
Remove ads

灰線: E1(x) = (1 − e −x)/
紅線: E2(x) = erf(x)
綠線: E3(x)
藍線: E4(x)
金線: E5(x).
廣義誤差函數為:
其中,E0(x)為通過原點的直線, 。E2(x) 即為誤差函數 erf(x)。
x > 0時,廣義誤差函數可以用Γ函數和 不完全Γ函數表示,
因此,誤差函數可以用不完全Γ函數表示為:
Remove ads
互補誤差函數的迭代積分定義為:
可以展開成冪級數:
滿足如下對稱性質:
和
函數表
註釋
參見
參考文獻
外部連結
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads





















![{\displaystyle \mathrm {erfc} (x)={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\left[1+\sum _{n=1}^{\infty }(-1)^{n}{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{(2x^{2})^{n}}}\right]={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n-1)!!}{(2x^{2})^{n}}},\,}](http://wikimedia.org/api/rest_v1/media/math/render/svg/802266cbf19574e452c0f388f9585fbb5d831064)

















![{\displaystyle \Phi (x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{\tfrac {-t^{2}}{2}}\,\mathrm {d} t={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]={\frac {1}{2}}\,\operatorname {erfc} \left(-{\frac {x}{\sqrt {2}}}\right)}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9c1d0724a58c2d7643ac79237496d4f6de3b1e9a)














