米塔-列夫勒函數
来自维基百科,自由的百科全书
米塔-列夫勒函數(Mittag-Leffler function)是一個特殊函數,常用於分數微積分方程,定義如下
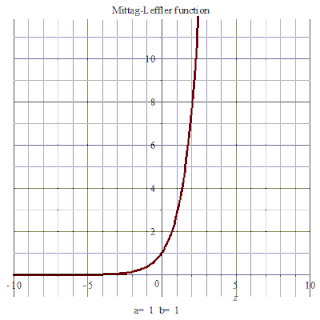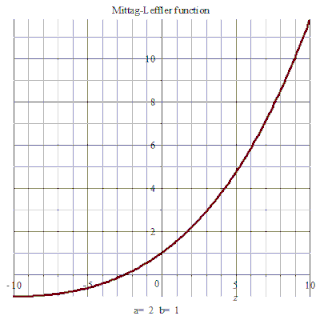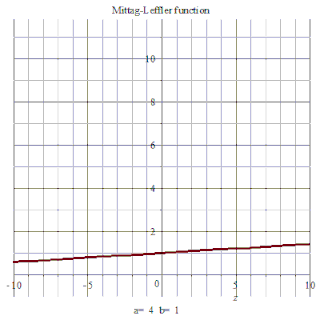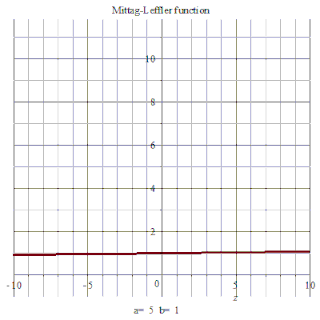


特例
對應 有
指數函數:
誤差函數:
雙曲餘弦:
對應 , :
- 有下列積分式
- ,
- ,
- .
參考文獻
- Mittag-Leffler, M.G.: Sur la nouvelle fonction E(x). C. R. Acad. Sci. Paris 137, 554–558 (1903)
- Mittag-Leffler, M.G.: Sopra la funzione E˛.x/. Rend. R. Acc. Lincei, (Ser. 5) 13, 3–5 (1904)
- Gorenflo R., Kilbas A.A., Mainardi F., Rogosin S.V., Mittag-Leffler Functions, Related Topics and Applications (Springer, New York, 2014) (頁面存檔備份,存於互聯網檔案館) 443 pages ISBN 978-3-662-43929-6
- Olver, F. W. J.; Maximon, L. C., 米塔-列夫勒函数, Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (編), NIST Handbook of Mathematical Functions, Cambridge University Press, 2010, ISBN 978-0521192255, MR2723248
- Igor Podlubny. chapter 1. Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, Some Methods of Their Solution and Some of Their Applications. Mathematics in Science and Engineering. Academic Press. 1998. ISBN 0-12-558840-2.
- Kai Diethelm. chapter 4. The analysis of fractional differential equations: an application-oriented exposition using differential operators of Caputo type. Lecture notes in mathematics. Heidelberg and New York: Springer-Verlag. 2010. ISBN 978-3-642-14573-5.
Wikiwand - on
Seamless Wikipedia browsing. On steroids.











