普朗克黑體輻射定律

在物理學中，普朗克黑體輻射定律（英語：Planck's law，Blackbody radiation law，也簡稱作普朗克定律或黑體輻射定律）是指在任意溫度${\displaystyle T\,}$下，從一個黑體中發射出的電磁輻射的輻射率與頻率彼此之間的關係。在這裏，輻射率是頻率${\displaystyle \nu }$的函數^[1]：

${\displaystyle I_{\nu }(\nu ,T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\frac {h\nu }{kT}}-1}}}$，

普朗克定律描述的黑體輻射在不同溫度下的頻譜

如果寫成波長的函數，則輻射率為^[1]

${\displaystyle I_{\lambda }(\lambda ,T)={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda kT}}-1}}}$；

其中，${\displaystyle I_{\nu }}$或${\displaystyle I_{\lambda }}$是輻射率，${\displaystyle \nu \,}$是頻率，${\displaystyle \lambda \,}$是波長，${\displaystyle T\,}$是黑體的溫度，${\displaystyle h\,}$是普朗克常數，${\displaystyle c\,}$是光速，${\displaystyle k\,}$是波茲曼常數。

注意這兩個函數具有不同的單位：第一個函數是描述單位頻率間隔內的輻射率，而第二個則是單位波長間隔內的輻射率。因而${\displaystyle I_{\nu }(\nu ,T)}$和${\displaystyle I_{\lambda }(\lambda ,T)}$並不等價。它們之間存在有如下關係：

${\displaystyle I_{\nu }(\nu ,T)\,d\nu =-I_{\lambda }(\lambda ,T)\,d\lambda }$。

通過單位頻率間隔和單位波長間隔之間的關係，這兩個函數可以相互轉換：

${\displaystyle d\nu =d\left({\frac {c}{\lambda }}\right)=c\,d\left({\frac {1}{\lambda }}\right)=-{\frac {c}{\lambda ^{2}}}\,d\lambda }$。

在低頻率極限，普朗克定律趨於瑞立-金斯定律，而在高頻率極限，普朗克定律趨於維恩近似。

馬克斯·普朗克於1900年發展出普朗克定律，並從實驗結果計算出所涉及的常數。後來，他又展示，當表達為能量分佈時，該分佈是電磁輻射在熱力學平衡下的唯一穩定分佈。^[2]當表達為能量分佈時，該分佈是熱力學平衡分佈家族的成員之一，其它成員為玻色–愛因斯坦分佈、費米–狄拉克分佈、麥克斯韋-波茲曼分佈等等。

概述

德國物理學家馬克斯·普朗克

電磁波波長和頻率的關係為^[3]

${\displaystyle \lambda ={c \over \nu }.}$

普朗克定律有時寫做能量密度頻譜的形式^[4]：

${\displaystyle u_{\nu }(\nu ,T)={4\pi \over c}I_{\nu }(\nu ,T)={\frac {8\pi h\nu ^{3}}{c^{3}}}~{\frac {1}{e^{\frac {h\nu }{kT}}-1}},}$

這是指單位頻率在單位體積內的能量，單位是焦耳／（立方米·赫茲）。對全頻域積分可得到與頻率無關的能量密度。一個黑體的輻射場可以被看作是光子氣體，此時的能量密度可由氣體的熱力學參數決定。

能量密度頻譜也可寫成波長的函數

${\displaystyle u_{\lambda }(\lambda ,T)={8\pi hc \over \lambda ^{5}}{1 \over e^{\frac {hc}{\lambda kT}}-1},}$

下表中給出了函數中每一個物理量的意義和單位：

物理量	含義	國際單位制	厘米-克-秒制
${\displaystyle I\,}$	輻射率，在單位時間內從單位表面積和單位立體角內以單位頻率間隔或單位波長間隔輻射出的能量	焦耳·秒-1·米-2·球面度 -1·赫茲-1，或焦耳·秒-1·米-2·球面度- 1·米-1	爾格·秒-1·厘米-2·赫茲-1·球面度-1
${\displaystyle \nu \,}$	頻率	赫茲 (Hz)	赫茲
${\displaystyle \lambda \,}$	波長	米 (m)	厘米（cm）
${\displaystyle T\,}$	黑體的溫度	開爾文 (K)	開爾文
${\displaystyle h\,}$	普朗克常數	焦耳·秒 (J·s)	爾格·秒（erg·s）
${\displaystyle c\,}$	光速	米/秒 (m/s)	厘米／秒（cm/s）
${\displaystyle e\,}$	自然對數的底，2.718281...	1	1
${\displaystyle k\,}$	波茲曼常數	焦耳／開爾文 (J/K)	爾格／開爾文 (erg/K)

推導

下面的推導並非普朗克的原始推導（來源^[4]），需要用到電動力學、量子力學和統計力學的有關概念。

考慮一個充滿了電磁輻射的邊長為${\displaystyle L\,}$的立方體：根據經典電動力學，在立方體壁表面的邊界條件為電場的平行分量和磁場的垂直分量都為零。類似於處於束縛態的粒子的波函數，立方體內部的電磁場也是滿足邊界條件的週期性本徵函數的線性疊加，在垂直於立方體壁表面的三個方向上各個本徵函數的波長分別為${\displaystyle \lambda _{1},}$ ${\displaystyle \lambda _{2}}$和${\displaystyle \lambda _{3},}$

${\displaystyle \lambda _{i}={\frac {2L}{n_{i}}},}$

這裏${\displaystyle n_{i}}$是非負整數。對於每一組${\displaystyle n_{i}}$值都有兩個線性無關的解（兩種不同的模）。根據量子力學中的諧振子理論，任意模式下的系統能階為

${\displaystyle E_{n_{1},n_{2},n_{3}}\left(r\right)=\left(r+{\frac {1}{2}}\right){\frac {hc}{2L}}{\sqrt {n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}}.\qquad {\mbox{(1)}}}$

這裏量子數${\displaystyle r\,}$可看作是立方體中的光子數，而兩種不同模式對應的是光子的兩種偏振態。注意到當光子數為零時能階不為零，這種電磁場的真空能量是一種量子效應，是產生卡西米爾效應的原因。下面我們計算在溫度${\displaystyle T\,}$下光子數為零時系統處於真空狀態下的內能。

根據統計力學，在特定模式下不同能階的機率分佈由下式給出

${\displaystyle P_{r}={\frac {e^{-\beta E\left(r\right)}}{Z\left(\beta \right)}}.}$

這裏

${\displaystyle \beta \ {\stackrel {\mathrm {def} }{=}}\ 1/\left(kT\right).}$

分母${\displaystyle Z(\beta )\,}$是系統在特定模式下的配分函數，它能夠使機率分佈${\displaystyle P_{r}\,}$歸一化。對正則系綜有

${\displaystyle Z\left(\beta \right)=\sum _{r=0}^{\infty }e^{-\beta E\left(r\right)}={\frac {e^{-{\frac {\beta \varepsilon }{2}}}}{1-e^{-\beta \varepsilon }}}.}$

這裏我們定義單個光子的能量為

${\displaystyle \varepsilon \ {\stackrel {\mathrm {def} }{=}}\ {\frac {hc}{2L}}{\sqrt {n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}},}$

系統的平均能量和配分函數的關係為

${\displaystyle \left\langle E\right\rangle =-{\frac {d\ln Z}{d\beta }}={\frac {\varepsilon }{2}}+{\frac {\varepsilon }{e^{\beta \varepsilon }-1}}.}$

這個公式是玻色-愛因斯坦統計的一個特例。由於光子是玻色子，任一能階對光子的數量沒有限制，系統的化學勢為零。

系統的總能量是平均能量${\displaystyle \left\langle E\right\rangle }$對所有可能的單光子態求和。考慮在熱力學極限下，立方體邊長${\displaystyle L\,}$趨於無窮大，這時單光子能量${\displaystyle \varepsilon }$近似成為連續值，我們將平均能量${\displaystyle \left\langle E\right\rangle }$對單光子的連續能量積分就可以得到系統的總能量，這就需要我們首先確定在任意給定的能量範圍內具有多少個光子態。假設處於能階${\displaystyle \varepsilon }$和${\displaystyle \varepsilon +d\varepsilon }$的單光子態總數為${\displaystyle g(\varepsilon )\,d\varepsilon }$（這裏${\displaystyle g(\varepsilon )}$是所謂光子的能態密度，其具體表達式還需另行計算），則系統的總能量為

${\displaystyle U=\int _{0}^{\infty }{\frac {\varepsilon }{e^{\beta \varepsilon }-1}}g(\varepsilon )\,d\varepsilon .\qquad {\mbox{(2)}}}$

為計算光子能態密度的表達式，我們將（1）式重寫成

${\displaystyle \varepsilon \ {\stackrel {\mathrm {def} }{=}}\ {\frac {hc}{2L}}n,}$

這裏${\displaystyle n\,}$是向量${\displaystyle {\vec {n}}=\left(n_{1},n_{2},n_{3}\right)}$的模

${\displaystyle n={\sqrt {n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}}.}$

每一個向量都對應有兩個光子態，換句話說，在給定的一個由向量${\displaystyle {\vec {n}}=\left(n_{1},n_{2},n_{3}\right)}$構成的希爾伯特空間中的光子態總數是這個空間體積的2倍。一個微小的能量區間${\displaystyle d\varepsilon }$對應着這個希爾伯特空間中一個薄球殼的厚度${\displaystyle dn=(2L/hc)d\varepsilon }$。由於向量${\displaystyle {\vec {n}}}$的分量不能為負值，能量區間實際上只能對應整個薄球殼總體積的1/8（這是因為向量有三個分量，每一個分量都為正數時的機率為1/8）。因而在能量區間${\displaystyle d\varepsilon }$上光子態總數${\displaystyle g(\varepsilon )\,d\varepsilon }$為

${\displaystyle g(\varepsilon )\,d\varepsilon =2{\frac {1}{8}}4\pi n^{2}\,dn={\frac {8\pi L^{3}}{h^{3}c^{3}}}\varepsilon ^{2}\,d\varepsilon .}$

將這個表達式代入（2）式，得到

${\displaystyle U=L^{3}{\frac {8\pi }{h^{3}c^{3}}}\int _{0}^{\infty }{\frac {\varepsilon ^{3}}{e^{\beta \varepsilon }-1}}\,d\varepsilon .\qquad {\mbox{(3)}}}$

注意到${\displaystyle L\,}$的三次方是立方體體積，因此可直接得到能量密度的表達式，將它寫成頻率的頻譜函數${\displaystyle u(\nu ,T)}$

${\displaystyle {\frac {U}{L^{3}}}=\int _{0}^{\infty }u(\nu ,T)\,d\nu ,}$

其中

${\displaystyle u(\nu ,T)={8\pi h\nu ^{3} \over c^{3}}{1 \over e^{h\nu /kT}-1}.}$

這裏${\displaystyle u(\nu ,T)}$即是黑體輻射的能量頻譜密度，其意義為單位頻率在單位體積內的能量。

如果寫成波長的函數，

${\displaystyle {\frac {U}{L^{3}}}=\int _{0}^{\infty }u(\lambda ,T)\,d\lambda ,}$

其中

${\displaystyle u(\lambda ,T)={8\pi hc \over \lambda ^{5}}{1 \over e^{hc/\lambda kT}-1}.}$

這是黑體輻射的能量密度頻譜的另一種形式，其意義為單位波長在單位體積內的能量。在玻色或費米氣體情形下對這一函數積分需要用到多對數函數展開。但這裏可以用初等函數的辦法得到一個近似形式，數學上做代換

${\displaystyle \varepsilon =kTx,}$

積分變量從而可寫成如下形式

${\displaystyle u(T)={\frac {8\pi (kT)^{4}}{(hc)^{3}}}J,}$

其中${\displaystyle J}$的表達式為

${\displaystyle J=\int _{0}^{\infty }{\frac {x^{3}}{e^{x}-1}}\,dx={\frac {\pi ^{4}}{15}}.}$

這一積分結果將後文附錄中做說明。因而得到立方體中電磁場的總能量為

${\displaystyle {U \over V}={\frac {8\pi ^{5}(kT)^{4}}{15(hc)^{3}}},}$

其中${\displaystyle V=L^{3}\,}$是立方體體積（注意：這個表達式不是斯特凡-波茲曼定律，它的含義並不是理想黑體在單位時間內從單位表面積輻射出的總能量，參見斯特凡-波茲曼定律條目）。由於輻射各向同性，並且以光速傳播，能量的輻射率（單位時間單位立體角所對應輻射行進截面積及單位頻率下輻射的能量）為

${\displaystyle I(\nu ,T)={\frac {u(\nu ,T)\,c}{4\pi }},}$

從而得到普朗克黑體輻射定律

${\displaystyle I(\nu ,T)={\frac {2h\nu ^{3}}{c^{2}}}~{\frac {1}{e^{h\nu /kT}-1}}.}$

歷史

參見：光子、能量均分定理和紫外災變

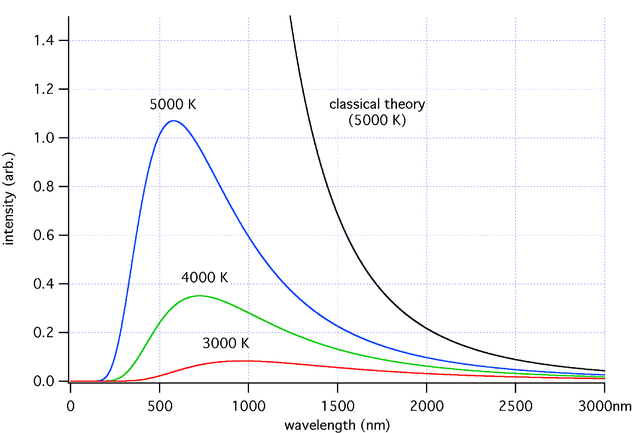
普朗克定律（綠）、維因近似（藍）和瑞立-金斯定律（紅）在頻域下的比較，可見維因近似在高頻區域和普朗克定律相符，瑞立-金斯定律在低頻區域和普朗克定律相符。

馬克斯·普朗克於1900年建立了黑體輻射定律的公式，並於1901年發表^[5]。其目的是改進由威廉·維因提出的維因近似（至於描述黑體輻射的另一公式：由瑞立勳爵和金斯爵士提出的瑞立-金斯定律，其建立時間要稍晚於普朗克定律。由此可見瑞立-金斯公式所導致的「紫外災變」並不是普朗克建立黑體輻射定律的動機，參見後文敘述）。維因近似在短波範圍內和實驗數據相當符合，但在長波範圍內偏差較大；而瑞立-金斯公式則正好相反。普朗克得到的公式則在全波段範圍內都和實驗結果符合得相當好。在推導過程中，普朗克考慮將電磁場的能量按照物質中帶電振子的不同振動模式分佈。得到普朗克公式的前提假設是這些振子的能量只能取某些基本能量單位的整數倍，這些基本能量單位只與電磁波的頻率${\displaystyle \nu \,}$有關，並且和頻率${\displaystyle \nu \,}$成正比。

${\displaystyle E=h\nu .\,}$

這即是普朗克的能量量子化假說，這一假說的提出比愛因斯坦為解釋光電效應而提出的光子概念還要至少早五年。然而普朗克並沒有像愛因斯坦那樣假設電磁波本身即是具有分立能量的量子化的波束，他認為這種量子化只不過是對於處在封閉區域所形成的腔（也就是構成物質的原子）內的微小振子而言的，用半經典的語言來說就是束縛態必然導出量子化。普朗克沒能為這一量子化假設給出更多的物理解釋，他只是相信這是一種數學上的推導手段，從而能夠使理論和經驗上的實驗數據在全波段範圍內符合。不過最終普朗克的量子化假說和愛因斯坦的光子假說都成為了量子力學的基石。

很多有關量子理論的大眾科普讀物，甚至某些物理學課本，在討論普朗克黑體輻射定律的歷史時都犯了嚴重的錯誤。儘管這些錯誤概念在四十多年前就已經被物理學史的研究者們指出，事實證明它們依然難以被消除。部分原因可能在於，普朗克最初量子化能量的動機並不是能用三言兩語就能夠道清的，這裏面的原因在現代人看來相當複雜，因而不易被外人所理解^[6]。丹麥物理學家Helge Kragh曾發表過一篇文章清晰地闡述了這種錯誤是如何發生的^[7]。

「紫外災變」：在經典統計理論中，能量均分定理預言黑體輻射的強度在紫外區域會發散至無窮大，這和事實嚴重違背

首先是儘管普朗克給出了量子化的電磁波能量表達式，普朗克並沒有將電磁波量子化，這在他1901年的論文以及這篇論文對他早先文獻的引用中就可以看到^[5]。他還在他的著作《熱輻射理論》（Theory of Heat Radiation）中平淡無奇地解釋說量子化公式中的普朗克常數（現代量子力學中的基本常數）只是一個適用於赫茲振盪器的普通常數。真正從理論上提出光量子的第一人是於1905年成功解釋光電效應的愛因斯坦，他假設電磁波本身就帶有量子化的能量，攜帶這些量子化的能量的最小單位叫光量子。1924年薩特延德拉·納特·玻色發展了光子的統計力學，從而在理論上推導了普朗克定律的表達式。

另一錯誤概念是，普朗克發展這一定律的動機並不是試圖解決「紫外災變」。「紫外災變」這一名稱是保羅·埃倫費斯特於1911年提出的，從時間上看這比普朗克定律的提出要晚十年之久。紫外災變是指將經典統計力學的能量均分定理應用於一個空腔中的黑體輻射（又叫做空室輻射或具空腔輻射）時，系統的總能量在紫外區域將變得發散並趨於無窮大，這顯然與實際不符。普朗克本人從未認為能量均分定理永遠成立，從而他根本沒有覺察到在黑體輻射中有任何「災變」存在——不過僅僅過了五年之後，這一問題隨着愛因斯坦、瑞立勳爵和金斯爵士的發現而就變得尖銳起來。

附錄

參見：黎曼ζ函數和Γ函數

有一個簡便方法計算下面的積分

${\displaystyle J=\int _{0}^{\infty }{\frac {x^{3}}{e^{x}-1}}\,dx}$

我們可以首先用${\displaystyle x^{n}\,}$替換式中的${\displaystyle x^{3}\,}$，計算一般形式下的積分

${\displaystyle \int _{0}^{\infty }{\frac {x^{n}}{e^{x}-1}}\,dx=\int _{0}^{\infty }{\frac {x^{n}e^{-x}}{1-e^{-x}}}\,dx}$

由於分母總是小於1，我們可以將它按${\displaystyle e^{-x}}$展開寫成收斂的幾何級數

${\displaystyle {\frac {1}{1-e^{-x}}}=\sum _{k=0}^{\infty }e^{-kx}.}$

這就是幾何級數的求和公式。等號左邊的表達式正是右邊的${\displaystyle 1+e^{-x}+e^{-2x}+e^{-3x}+\cdots .}$求和結果，右邊的幾何級數公比為${\displaystyle e^{-x}}$.

從而得到

${\displaystyle \int _{0}^{\infty }x^{n}e^{-x}\sum _{k=0}^{\infty }e^{-kx}\,dx.}$

表達式乘以${\displaystyle e^{-x}}$後相當於將${\displaystyle e^{-x}+e^{-2x}+e^{-3x}+\cdots }$變成${\displaystyle e^{-2x}+e^{-3x}+e^{-4x}+\cdots }$，因而我們將求和符號中的序號加1，並消去原先的${\displaystyle e^{-x}}$:

${\displaystyle \int _{0}^{\infty }x^{n}\sum _{k=1}^{\infty }e^{-kx}\,dx.}$

通過變量替換${\displaystyle u=kx}$，我們得到${\displaystyle x^{n}={\frac {u^{n}}{k^{n}}}}$以及${\displaystyle dx={\frac {du}{k}}}$，積分式進一步寫成

${\displaystyle \int _{0}^{\infty }{\frac {u^{n}}{k^{n}}}\sum _{k=1}^{\infty }e^{-u}{\frac {du}{k}}}$

即

${\displaystyle \int _{0}^{\infty }u^{n}\sum _{k=1}^{\infty }{\frac {1}{k^{n+1}}}e^{-u}du.}$

形如上式的積分是收斂的，我們將求和的部分移到積分之外：

${\displaystyle \sum _{k=1}^{\infty }{\frac {1}{k^{n+1}}}\int _{0}^{\infty }u^{n}e^{-u}\,du.}$

前面的求和係數正是黎曼ζ函數${\displaystyle \zeta (n+1)}$，而後面的積分正是Γ函數${\displaystyle \Gamma (n+1)}$。從而我們得到一個一般的關係式：

${\displaystyle \int _{0}^{\infty }{\frac {x^{n}}{e^{x}-1}}\,dx=\zeta (n+1)\Gamma {\left(n+1\right)}.}$

或等價為

${\displaystyle \int _{0}^{\infty }{\frac {x^{n-1}}{e^{x}-1}}\,dx=\zeta {\left(n\right)}\Gamma {\left(n\right)}.}$

對於我們所需要的積分，積分式的分子為${\displaystyle x^{3}}$，因此代入上面等式中得到

${\displaystyle J=\zeta {\left(4\right)}\Gamma {\left(4\right)}={\frac {\pi ^{4}}{90}}\times 6={\frac {\pi ^{4}}{15}}.}$

這裏我們用到了

${\displaystyle \zeta {\left(4\right)}=\sum _{n=1}^{\infty }{\frac {1}{n^{4}}}=\pi ^{4}/90}$

和${\displaystyle \Gamma (n+1)=n!}$。（參見黎曼ζ函數和Γ函數的有關性質）。

參考文獻

1. Rybicki & Lightman 1979，第22頁
2. Planck 1914，第42頁
3. (Rybicki & Lightman 1979，第1頁)
4. Brehm, J.J. and Mullin, W.J., "Introduction to the Structure of Matter: A Course in Modern Physics," (Wiley, New York, 1989) ISBN 0-471-60531-X.
5. Planck, Max, "On the Law of Distribution of Energy in the Normal Spectrum 互聯網檔案館的存檔，存檔日期2008-04-18.". Annalen der Physik, vol. 4, p. 553 ff (1901)
6. 關於究竟是什麼動機致使普朗克建立了量子化的能量這一歷史爭論，請參看
   Kuhn, Thomas. Black-Body Theory and the Quantum Discontinuity: 1894-1912. Clarendon Press, Oxford. 1978. ISBN 0-226-45800-8.
   Galison, Peter. Kuhn and the Quantum Controversy. British Journal for the Philosophy of Science. 1981, 32 (1): 71–85.
7. Kragh, Helge Max Planck: The reluctant revolutionary （頁面存檔備份，存於互聯網檔案館） Physics World, December 2000.

目錄

• Adkins, C. J. Equilibrium Thermodynamics 3rd. Cambridge University Press. 1983. ISBN 0-521-25445-0.
• Bohr, N. On the constitution of atoms and molecules (PDF). Philosophical Magazine. 1913, 26 (153): 1–25 [2018-06-12]. doi:10.1080/14786441308634993. （原始內容存檔 (PDF)於2017-08-09）.
• Bohren, C. F.; Clothiaux, E. E. Fundamentals of Atmospheric Radiation. Wiley-VCH. 2006. ISBN 3-527-40503-8.
• Boltzmann, L. Über die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung, respective den Sätzen über das Wärmegleichgewicht. Sitzungsberichte Mathematisch-Naturwissenschaftlichen Classe der kaiserlichen Akademie der Wissenschaften in Wien. 1878, 76 (2): 373–435.
• Born, M.; Wolf, E. Principles of Optics 7th. Cambridge University Press. 1999. ISBN 0-521-64222-1.
• Born, M.; Jordan, P. Zur Quantenmechanik. Zeitschrift für Physik. 1925, 34: 858–888. Bibcode:1925ZPhy...34..858B. doi:10.1007/BF01328531. Translated in part as "On quantum mechanics" in van der Waerden, B. L. Sources of Quantum Mechanics. North-Holland Publishing. 1967: 277–306.
• Bose, Satyendra Nath. Plancks Gesetz und Lichtquantenhypothese. Zeitschrift für Physik. 1924, 26: 178–181. Bibcode:1924ZPhy...26..178B. doi:10.1007/BF01327326 （德語）.
• Brehm, J. J.; Mullin, W. J. Introduction to the Structure of Matter. John Wiley & Sons. 1989. ISBN 0-471-60531-X.
• Brillouin, L. Relativity Reexamined. Academic Press. 1970. ISBN 978-0-12-134945-5.
• Caniou, J. Passive Infrared Detection: Theory and Applications. Springer. 1999. ISBN 978-0-7923-8532-5.
• Chandrasekhar, S. Radiative Transfer Revised reprint. Dover Publications. 1960 [1950]. ISBN 978-0-486-60590-6.
• Cotton, A. The present status of Kirchhoff's law. The Astrophysical Journal. 1899, 9: 237–268. Bibcode:1899ApJ.....9..237C. doi:10.1086/140585.
• Crova, A. P. P. Étude des radiations émises par les corps incandescents. Mesure optique des hautes températures. Annales de chimie et de physique. Série 5. 1880, 19: 472–550 [2018-06-12]. （原始內容存檔於2020-05-20）.
• Dougal, R. C. The presentation of the Planck radiation formula (tutorial). Physics Education. 1976, 11 (6): 438–443. Bibcode:1976PhyEd..11..438D. doi:10.1088/0031-9120/11/6/008.
• Ehrenfest, P. Welche Züge der Lichtquantenhypothese spielen in der Theorie der Wärmestrahlung eine wesentliche Rolle?. Annalen der Physik. 1911, 36 (11): 91–118. Bibcode:1911AnP...341...91E. doi:10.1002/andp.19113411106.
• Ehrenfest, P.; Kamerlingh Onnes, H. Simplified deduction of the formula from the theory of combinations which Planck uses as the basis of his radiation theory. Proceedings of the Royal Dutch Academy of Sciences in Amsterdam. 1914, 17 (2): 870–873. Bibcode:1914KNAB...17..870E.
• Einstein, A. Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt. Annalen der Physik. 1905, 17 (6): 132–148 [2018-06-12]. Bibcode:1905AnP...322..132E. doi:10.1002/andp.19053220607. （原始內容存檔於2017-07-22）. Translated in Arons, A. B.; Peppard, M. B. Einstein's proposal of the photon concept: A translation of the Annalen der Physik paper of 1905 (PDF). American Journal of Physics. 1965, 33 (5): 367 [2018-06-12]. Bibcode:1965AmJPh..33..367A. doi:10.1119/1.1971542. （原始內容 (PDF)存檔於2016-03-04）.
• Einstein, A. Zur Quantentheorie der Strahlung. Mitteilungen der Physikalischen Gesellschaft Zürich. 1916, 18: 47–62. and a nearly identical version Einstein, A. Zur Quantentheorie der Strahlung. Physikalische Zeitschrift. 1917, 18: 121–128. Bibcode:1917PhyZ...18..121E. Translated in ter Haar, D. The Old Quantum Theory. Pergamon Press. 1967: 167–183. LCCN 66029628. See also [1].
• Einstein, A. The Collected Papers of Albert Einstein 3. English translation by Beck, A. Princeton University Press. 1993. ISBN 0-691-10250-3.
• Feynman, R. P.; Leighton, R. B.; Sands, M. The Feynman Lectures on Physics, Volume 1. Addison-Wesley. 1963. ISBN 0-201-02010-6.
• Fischer, T. Topics: Derivation of Planck's Law. ThermalHUB. 1 November 2011 [2015-06-19]. （原始內容存檔於2020-11-25）.
• Goody, R. M.; Yung, Y. L. Atmospheric Radiation: Theoretical Basis 2nd. Oxford University Press. 1989. ISBN 978-0-19-510291-8.
• Guggenheim, E. A. Thermodynamics. An Advanced Treatment for Chemists and Physicists 5th revised. North-Holland Publishing Company. 1967.
• Haken, H. Light Reprint. Amsterdam: North-Holland Publishing. 1981. ISBN 0-444-86020-7.
• Hapke, B. Theory of Reflectance and Emittance Spectroscopy. Cambridge University Press, Cambridge UK. 1993. ISBN 0-521-30789-9.
• Heisenberg, W. Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. Zeitschrift für Physik. 1925, 33: 879–893. Bibcode:1925ZPhy...33..879H. doi:10.1007/BF01328377. Translated as "Quantum-theoretical Re-interpretation of kinematic and mechanical relations" in van der Waerden, B. L. Sources of Quantum Mechanics. North-Holland Publishing. 1967: 261–276.
• Heisenberg, W. The Physical Principles of the Quantum Theory. Eckart, C.; Hoyt, F. C. (transl.). University of Chicago Press. 1930.
• Hermann, A. The Genesis of Quantum Theory. Nash, C.W. (transl.). MIT Press. 1971. ISBN 0-262-08047-8. a translation of Frühgeschichte der Quantentheorie (1899–1913), Physik Verlag, Mosbach/Baden, 1969.
• Hettner, G. Die Bedeutung von Rubens Arbeiten für die Plancksche Strahlungsformel. Naturwissenschaften. 1922, 10 (48): 1033–1038. Bibcode:1922NW.....10.1033H. doi:10.1007/BF01565205.
• Jammer, M. The Conceptual Development of Quantum Mechanics second. Tomash Publishers/American Institute of Physics. 1989. ISBN 0-88318-617-9.
• Jauch, J. M.; Rohrlich, F. The Theory of Photons and Electrons. The Relativistic Quantum Field Theory of Charged Particles with Spin One-half second printing of second. pringer. 1980 [1955]. ISBN 0-387-07295-0.
• Jeans, J. H. The Distribution of Molecular Energy. Philosophical Transactions of the Royal Society A. 1901, 196 (274–286): 397. Bibcode:1901RSPTA.196..397J. JSTOR 90811. doi:10.1098/rsta.1901.0008.
• Jeans, J. H. XI. On the partition of energy between matter and æther. Philosophical Magazine. 1905a, 10 (55): 91. doi:10.1080/14786440509463348.
• Jeans, J. H. On the Application of Statistical Mechanics to the General Dynamics of Matter and Ether. Proceedings of the Royal Society Ａ. 1905b, 76 (510): 296. Bibcode:1905RSPSA..76..296J. JSTOR 92714. doi:10.1098/rspa.1905.0029.
• Jeans, J. H. A Comparison between Two Theories of Radiation. Nature. 1905c, 72 (1865): 293. Bibcode:1905Natur..72..293J. doi:10.1038/072293d0.
• Jeans, J. H. On the Laws of Radiation. Proceedings of the Royal Society A. 1905d, 76 (513): 545. Bibcode:1905RSPSA..76..545J. JSTOR 92704. doi:10.1098/rspa.1905.0060.
• Jeffreys, H. Scientific Inference 3rd. Cambridge University Press. 1973. ISBN 978-0-521-08446-8.
• Kangro, H. Early History of Planck's Radiation Law. Taylor & Francis. 1976. ISBN 0-85066-063-7.
• Karplus, R.; Neuman, M. The Scattering of Light by Light. Physical Review. 1951, 83 (4): 776–784. Bibcode:1951PhRv...83..776K. doi:10.1103/PhysRev.83.776.
• Kirchhoff, G. R. Über die Fraunhofer'schen Linien. Monatsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin. 1860a: 662–665.
• Kirchhoff, G. R. Über den Zusammenhang zwischen Emission und Absorption von Licht und Wärme. Monatsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin. 1860b: 783–787.
• Kirchhoff, G. R. Über das Verhältniss zwischen dem Emissionsvermögen und dem Absorptionsvermögen der Körper für Wärme and Licht. Annalen der Physik und Chemie. 1860c, 109 (2): 275–301. Bibcode:1860AnP...185..275K. doi:10.1002/andp.18601850205. Translated by Guthrie, F. as Kirchhoff, G. R. On the relation between the radiating and absorbing powers of different bodies for light and heat. Philosophical Magazine. Series 4. 1860, 20: 1–21.
• Kirchhoff, G. R., Über das Verhältniss zwischen dem Emissionsvermögen und dem Absorptionsvermögen der Körper für Wärme und Licht, Gessamelte Abhandlungen, Johann Ambrosius Barth: 571–598, 1862
• Kittel, C.; Kroemer, H. Thermal Physics 2nd. W. H. Freeman. 1980. ISBN 0-7167-1088-9.
• Klein, M. J. Max Planck and the beginnings of the quantum theory. Archive for History of Exact Sciences. 1962, 1 (5): 459–479. doi:10.1007/BF00327765.
• Kragh, H. Quantum Generations. A History of Physics in the Twentieth Century. Princeton University Press. 1999. ISBN 0-691-01206-7.
• Kragh, H. Max Planck: The reluctant revolutionary. Physics World. December 2000 [2018-06-12]. （原始內容存檔於2012-04-01）.
• Kramm, Gerhard; Mölders, N. Planck's Blackbody Radiation Law: Presentation in Different Domains and Determination of the Related Dimensional Constant. Journal of the Calcutta Mathematical Society. 2009, 5 (1–2): 27–61. Bibcode:2009arXiv0901.1863K. arXiv:0901.1863 .
• Kuhn, T. S. Black–Body Theory and the Quantum Discontinuity. Oxford University Press. 1978. ISBN 0-19-502383-8.
• Landsberg, P. T. Thermodynamics with Quantum Statistical Illustrations. Interscience Publishers. 1961.
• Landsberg, P. T. Thermodynamics and Statistical Mechanics. Oxford University Press. 1978. ISBN 0-19-851142-6.
• Lewis, G. N. The Conservation of Photons. Nature. 1926, 118 (2981): 874. Bibcode:1926Natur.118..874L. doi:10.1038/118874a0.
• Loudon, R. The Quantum Theory of Light 3rd. Oxford University Press. 2000 [2018-06-12]. ISBN 0-19-850177-3. （原始內容存檔於2020-05-20）.
• Lowen, A. N.; Blanch, G. Tables of Planck's radiation and photon functions. Journal of the Optical Society of America. 1940, 30 (2): 70. Bibcode:1940JOSA...30...70L. doi:10.1364/JOSA.30.000070.
• Lummer, O.; Kurlbaum, F. Der electrisch geglühte "absolut schwarze" Körper und seine Temperaturmessung. Verhandlungen der Deutschen Physikalischen Gesellschaft. 1898, 17: 106–111.
• Lummer, O.; Pringsheim, E. 1. Die Vertheilung der Energie in Spectrum des schwarzen Körpers und des blanken Platins; 2. Temperaturbestimmung fester glühender Körper. Verhandlungen der Deutschen Physikalischen Gesellschaft. 1899, 1: 215–235.
• Lummer, O.; Kurlbaum, F. Der elektrisch geglühte "schwarze" Körper. Annalen der Physik. 1901, 310 (8): 829–836. Bibcode:1901AnP...310..829L. doi:10.1002/andp.19013100809.
• Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics. Cambridge University Press. 1995. ISBN 0-521-41711-2.
• Mehra, J.; Rechenberg, H. The Historical Development of Quantum Theory 1. Springer-Verlag. 1982. ISBN 0-387-90642-8. |issue=被忽略 (幫助)
• Messiah, A. Quantum Mechanics. Temmer, G. G. (transl.). John Wiley & Sons. 1958.
• Michelson, V. A. Theoretical essay on the distribution of energy in the spectra of solids. Philosophical Magazine. Series 5. 1888, 25 (156): 425–435. doi:10.1080/14786448808628207.
• Mihalas, D.; Weibel-Mihalas, B. Foundations of Radiation Hydrodynamics. Oxford University Press. 1984. ISBN 0-19-503437-6.
• Milne, E. A. Thermodynamics of the Stars. Handbuch der Astrophysik. 1930, 3 (1): 63–255.
• Mohr, P. J.; Taylor, B. N.; Newell, D. B. CODATA Recommended Values of the Fundamental Physical Constants: 2010 (PDF). Reviews of Modern Physics. 2012, 84 (4): 1527–1605 [2018-06-12]. Bibcode:2012RvMP...84.1527M. arXiv:1203.5425 . doi:10.1103/RevModPhys.84.1527. （原始內容存檔 (PDF)於2018-06-12）.
• Paltridge, G. W.; Platt, C. M. R. Radiative Processes in Meteorology and Climatology. Elsevier. 1976. ISBN 0-444-41444-4.
• Paschen, F. Über Gesetzmäßigkeiten in den Spectren fester Körper und über ein neue Bestimmung der Sonnentemperatur. Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen (Mathematisch-Physikalische Klasse). 1895: 294–304.
• Pauli, W. Enz, C. P. , 編. Wave Mechanics. Margulies, S.; Lewis, H. R. (transl.). MIT Press. 1973. ISBN 0-262-16050-1.
• Planck, M. Über eine Verbesserung der Wien'schen Spectralgleichung. Verhandlungen der Deutschen Physikalischen Gesellschaft. 1900a, 2: 202–204. Translated in ter Haar, D. On an Improvement of Wien's Equation for the Spectrum. The Old Quantum Theory (PDF). Pergamon Press. 1967: 79–81 [2018-06-12]. LCCN 66029628. （原始內容 (PDF)存檔於2016-10-10）.
• Planck, M. Zur Theorie des Gesetzes der Energieverteilung im Normalspectrum. Verhandlungen der Deutschen Physikalischen Gesellschaft. 1900b, 2: 237–245. Translated in ter Haar, D. The Old Quantum Theory (PDF). Pergamon Press: 82. 1967 [2014-02-08]. LCCN 66029628. （原始內容 (PDF)存檔於2016-09-20）.
• Planck, M. Entropie und Temperatur strahlender Wärme. Annalen der Physik. 1900c, 306 (4): 719–737. Bibcode:1900AnP...306..719P. doi:10.1002/andp.19003060410.
• Planck, M. Über irreversible Strahlungsvorgänge. Annalen der Physik. 1900d, 306 (1): 69–122. Bibcode:1900AnP...306...69P. doi:10.1002/andp.19003060105.
• Planck, M. Über das Gesetz der Energieverteilung im Normalspektrum. Annalen der Physik. 1901, 4 (3): 553. Bibcode:1901AnP...309..553P. doi:10.1002/andp.19013090310. Translated in Ando, K. On the Law of Distribution of Energy in the Normal Spectrum (PDF). [2011-10-13]. （原始內容 (PDF)存檔於6 October 2011）.
• Planck, M. Vorlesungen über die Theorie der Wärmestrahlung. Johann Ambrosius Barth. 1906. LCCN 07004527.
• Planck, M. The Theory of Heat Radiation. Masius, M. (transl.) 2nd. P. Blakiston's Son & Co. 1914. OL 7154661M.
• Planck, M. Eight Lectures on Theoretical Physics. Wills, A. P. (transl.). Dover Publications. 1915. ISBN 0-486-69730-4.
• Planck, M. Zur Geschichte der Auffindung des physikalischen Wirkungsquantums. Naturwissenschaften. 1943, 31 (14–15): 153–159. Bibcode:1943NW.....31..153P. doi:10.1007/BF01475738.
• Rayleigh, Lord. LIII. Remarks upon the law of complete radiation. Philosophical Magazine. Series 5. 1900, 49 (301): 539. doi:10.1080/14786440009463878.
• Rayleigh, Lord. The Dynamical Theory of Gases and of Radiation. Nature. 1905, 72 (1855): 54–55. Bibcode:1905Natur..72...54R. doi:10.1038/072054c0.
• Razavy, M. Heisenberg's Quantum Mechanics. World Scientific. 2011. ISBN 978-981-4304-10-8.
• Rubens, H.; Kurlbaum, F. Über die Emission langer Wellen durch den schwarzen Körper. Verhandlungen der Deutschen Physikalischen Gesellschaft. 1900a, 2: 181.
• Rubens, H.; Kurlbaum, F. Über die Emission langwelliger Wärmestrahlen durch den schwarzen Körper bei verschiedenen Temperaturen. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin. 1900b: 929–941. Translated in Rubens, H.; Kurlbaum, F. On the heat-radiation of long wave-length emitted by black bodies at different temperatures. The Astrophysical Journal. 1901, 14: 335–348. Bibcode:1901ApJ....14..335R. doi:10.1086/140874.
• Rybicki, G. B.; Lightman, A. P. Radiative Processes in Astrophysics. John Wiley & Sons. 1979 [2018-06-12]. ISBN 0-471-82759-2. （原始內容存檔於2021-03-09）.
• Sharkov, E. A. Black-body radiation. Passive Microwave Remote Sensing of the Earth (PDF). Springer. 2003 [2018-06-12]. ISBN 978-3-540-43946-2. （原始內容存檔 (PDF)於2021-02-17）.
• Schiff, L. I. Quantum Mechanics. McGraw-Hill. 1949.
• Schirrmacher, A. Experimenting theory: the proofs of Kirchhoff's radiation law before and after Planck. Münchner Zentrum für Wissenschafts und Technikgeschichte. 2001.
• Schwinger, J. Englert, B.-G. , 編. Quantum Mechanics: Symbolism of Atomic Measurements. Springer. 2001. ISBN 3-540-41408-8.
• Scully, M. O.; Zubairy, M. S. Quantum Optics. Cambridge University Press. 1997. ISBN 0-521-43458-0.
• Siegel, D. M. Balfour Stewart and Gustav Robert Kirchhoff: two independent approaches to "Kirchhoff's radiation law". Isis. 1976, 67 (4): 565–600. doi:10.1086/351669.
• Siegel, R.; Howell, J. R. Thermal Radiation Heat Transfer, Volume 1 4th. Taylor & Francis. 2002 [2018-06-12]. ISBN 978-1-56032-839-1. （原始內容存檔於2020-05-20）.
• Sommerfeld, A. Atomic Structure and Spectral Lines. Brose, H. L. (transl.) from 3rd German. Methuen Publishing. 1923 [2018-06-12]. （原始內容存檔於2020-05-20）.
• Stehle, P. Order, Chaos, Order. The Transition from Classical to Quantum Physics. Oxford University Press. 1994. ISBN 0-19-507513-7.
• Stewart, B. An account of some experiments on radiant heat. Transactions of the Royal Society of Edinburgh. 1858, 22: 1–20.
• ter Haar, D. The Old Quantum Theory. Pergamon Press. 1967. LCCN 66-029628.
• Thornton, S. T.; Rex, A. F. Modern Physics. Thomson Learning. 2002. ISBN 0-03-006049-4.
• Tisza, L. Generalized Thermodynamics. MIT Press. 1966.
• Tommasini, D.; Ferrando, F.; Michinel, H.; Seco, M. Detecting photon-photon scattering in vacuum at exawatt lasers. Physical Review A. 2008, 77: 042101. Bibcode:2008PhRvA..77a2101M. arXiv:quant-ph/0703076 . doi:10.1103/PhysRevA.77.012101.
• Tyndall, J. Über leuchtende und dunkle Strahlung. Annalen der Physik und Chemie. 1865a, 200: 36–53. Bibcode:1865AnP...200...36T. doi:10.1002/andp.18652000103.
• Tyndall, J. Heat considered as a Mode of Motion. D. Appleton & Company. 1865b.
• Wien, W. Über die Energievertheilung im Emissionsspectrum eines schwarzen Körpers. Annalen der Physik und Chemie. 1896, 294 (8): 662–669. Bibcode:1896AnP...294..662W. doi:10.1002/andp.18962940803.
• Wilson, A. H. Thermodynamics and Statistical Mechanics. Cambridge University Press. 1957.

參見

• 黑體 (熱力學)
• 維因位移定律
• 維因近似
• 瑞立-金斯定律
• 盒中氣體

延伸閱讀

• Peter C. Milonni. The Quantum Vacuum. Academic Press. 1994.

外部連結

• Summary of Radiation
• Radiation of a Blackbody - interactive simulation to play with Planck's law
• Scienceworld entry on Planck's Law