蟲洞

蟲洞（英語：Wormhole），又稱愛因斯坦-羅森橋（英語：Einstein—Rosen bridge），是一種連接時空中不同點的理論結構，它基於愛因斯坦場方程式的特殊解。它們於1916年由路德維希·弗拉姆（英語：Ludwig Flamm）首次提出，並於1935年由阿爾伯特·愛因斯坦和內森·羅森再次提出。因此，它們也被稱為愛因斯坦-羅森橋。^[2] 蟲洞一詞是由約翰·阿奇博爾德·惠勒在1957年創造的，^[3] 而蟲洞這個名字有「蟲咬的洞」的意思，其舉例來自如果一隻蟲要蘋果表面移動，比起沿着表面爬，不如直接從果肉穿過距離更短。^[4]

若地面附近有一個蟲洞，它可能是這樣的^[1]

蟲洞可以想像成一條隧道，其兩端位於時空的不同點（可能是不同的位置和時間）。

蟲洞與廣義相對論是相容的，但蟲洞是否真的存在還有待觀察。許多科學家假設蟲洞只是第四空間維度的投影，類似於二維生物如何只能體驗三維物體的一部分^[5] 克萊因瓶提供了這種結構的一個眾所周知的類比，在三維渲染時顯示一個孔，而不是在四維或更高維度上。

理論上，一個蟲洞可能連接十億光年這樣的極遠距離，也可能連接幾米這樣的短距離，或者不同的時間點，甚至不同的宇宙。^[6]

1995年，馬特·維瑟（英語：Matt Visser）提出，如果在早期宇宙中生成負質量/負能量的宇宙弦，宇宙中可能存在許多蟲洞。^[7][8] 一些物理學家，例如法蘭克·迪普勒和基普·索恩，提出了如何人工製造蟲洞。^{[來源請求]}

可視化

被視覺化為2D的蟲洞

對於蟲洞的簡化概念，空間可以被想像為二維表面。蟲洞會出現在該表面上的一個洞，通向一個三維管道（圓柱體的內表面），然後重新出現在二維表面上的另一個位置，並有一個與入口類似的洞。實際的蟲洞與此類似，但空間維度增加了一維。例如，入口和出口點可以被視為三維空間中的球形孔，而不是二維平面上的圓形孔，通向類似於球體的四維「管道」。 ^{[需要引用]}

另一種蟲洞在二維環境的模擬

想像蟲洞的另一種方式是拿一張紙並在紙的一側畫兩個稍遠的點。這張紙代表時空連續體中的一個平面，而這兩個點代表要行進的距離，但理論上，蟲洞可以通過摺疊該平面（即紙張）使這兩個點接觸來連接這兩個點。這樣，由於兩點現在相切，穿越距離就會變得容易得多。 ^{[需要引用]}

發展過程

史瓦西蟲洞的「嵌入圖」

史瓦西蟲洞

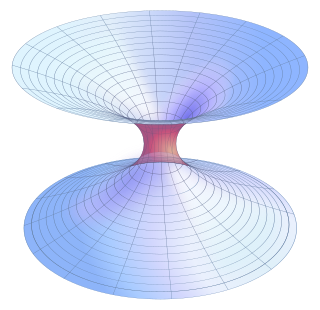
發現的第一種蟲洞解決方案是史瓦西蟲洞，它存在於描述永恆黑洞的史瓦西度規中，但人們發現它塌縮得太快，任何東西都無法從一端穿過到另一端。人們認為，只有使用具有負能量密度的奇異物質來穩定蟲洞，才有可能形成可以雙向穿越的蟲洞，又稱為可穿越蟲洞。 ^[9]後來，物理學家報告稱，微觀可穿越蟲洞可能是可能的，而且不需要任何奇異物質，而只需要帶電費米子物質，其質量足夠小，不會塌縮成帶電黑洞。 ^{[10] [11] [12]}儘管這種蟲洞（如果可能的話）可能僅限於資訊傳輸，但如果現實可以用蘭德爾-桑德拉姆模型 2 （一種與弦理論一致的基於膜的理論）廣泛描述，那麼人類可穿越的蟲洞可能存在。 ^[13]

愛因斯坦–羅森橋

愛因斯坦-羅森橋(或ER 橋) 以阿爾伯特·愛因斯坦和內森·羅森的名字命名， 是空間區域之間的連接，可以建模為愛因斯坦場方程式的真空解，現在被理解為史瓦西度量的最大擴展版本的內在部分，描述一個沒有電荷和旋轉的永恆黑洞。這裏，「最大程度延伸」指的是時空不應該有任何「邊緣」：對於自由落體粒子的任何可能軌跡（沿着時空中的測地線），這條路徑應該可以任意延伸到粒子的未來或過去。

為了滿足這一要求，事實證明，除了粒子從外部穿過事件視界時進入的黑洞內部區域之外，還必須有一個單獨的白洞內部區域，以便我們推斷外部觀察者看到的粒子從事件視界上升起的軌跡。 ^[14]正如最大延伸時空有兩個獨立的內部區域一樣，也存在兩個獨立的外部區域，有時被稱為兩個不同的「宇宙」，第二個宇宙使我們能夠推斷兩個內部區域中一些可能的粒子軌跡。這意味着黑洞內部區域可以包含來自任一宇宙的混合粒子（因此從一個宇宙落入的觀察者可能能夠看到從另一個宇宙落入的光），同樣，來自白洞內部區域的粒子可以逃逸到任一宇宙。所有四個區域都可以在使用克魯斯卡爾-塞凱列斯坐標的時空圖中看到。

在這個時空中，可以提出這樣的坐標系：如果選擇一個常數時間的超曲面（一組具有相同時間坐標的點，使得曲面上的每個點都有一個類空間分離，從而產生所謂的「類空間曲面」）並繪製一個描繪當時空間曲率的「嵌入圖」，則嵌入圖將看起來就像連接兩個外部區域的管道，稱為「愛因斯坦-羅森橋」。史瓦西度規描述的是從外部觀察者的角度永遠存在的理想黑洞；而由塌縮恆星在特定時間形成的更現實的黑洞則需要不同的度規。當墜落的恆星物質被添加到黑洞地理圖上時，它會移除對應於白洞內部區域的部分圖表，以及對應於另一個宇宙的部分圖表。

愛因斯坦-羅森橋由路德維希·弗拉姆於 1916 年發現， ^[15]就在史瓦西發表他的解法幾個月後。後來，阿爾伯特·愛因斯坦和他的同事內森·羅森重新發現了愛因斯坦-羅森橋，並於 1935 年發表了他們的成果。 ^[16] 1962 年，約翰·阿奇博爾德·惠勒 (John Archibald Wheeler)和羅拔·W·富勒 (Robert W. Fuller)發表了一篇論文^[17] ，指出這種類型的蟲洞如果連接同一宇宙的兩個部分，則是不穩定的，並且它會很快切斷，使得從一個外部區域落入的光（或任何速度比光慢的粒子）無法到達另一個外部區域。

根據廣義相對論，足夠緻密的質量的重力塌縮會形成一個奇異的史瓦西黑洞。然而，在愛因斯坦-嘉當-夏馬-基布爾重力理論中，它形成了一個規則的愛因斯坦-羅森橋。該理論通過消除仿射聯絡對稱性的約束並將其反對稱部分扭轉張量視為動態變量，擴展了廣義相對論。扭轉自然地解釋了物質的量子力學、內在角動量（自旋）。扭轉和狄拉克旋量之間的最小耦合會產生排斥性的自旋-自旋相互作用，這在極高密度的費米子物質中非常重要。這種相互作用阻止了重力奇異點（例如黑洞）的形成。相反，塌縮的物質會達到巨大但有限的密度並反彈，形成橋的另一側。 ^[18]

儘管史瓦西蟲洞無法雙向穿越，但它的存在啟發了基普·索恩想像通過用奇異物質（具有負質量/能量的物質）將史瓦西蟲洞的「喉嚨」打開，從而形成可穿越的蟲洞。 ^[19]

其他不可穿越的蟲洞包括勞侖茲蟲洞（由約翰·阿奇博爾德·惠勒於 1957 年首次提出）、在用勞侖茲流形描繪的廣義相對論時空流形中創建時空泡沫的蟲洞^[20] ，以及歐幾里得蟲洞（以歐幾里得流形命名，歐幾里得流形是黎曼流形的一種結構）。

可穿越的蟲洞

卡西米爾效應表明，量子場論允許空間某些區域的能量密度相對於普通物質的真空能量為負，並且理論上已經證明，量子場論允許能量在給定點任意為負的狀態。 ^[21]許多物理學家，如史蒂芬·霍金、 ^[22]基普·索恩、 ^[23]等人， ^{[24] [25] [26]}認為，這種效應可能使可穿越蟲洞成為穩定。 ^[27]在廣義相對論和量子力學的背景下，唯一已知的、理論上預測會形成蟲洞的自然過程是由胡安·馬爾達西那和倫納德·蘇士侃在他們的ER = EPR猜想中提出的。量子泡沫假說有時被用來表明微小蟲洞可能在普朗克尺度上自發出現和消失， ^{[28] :494–496[29]}此類蟲洞的穩定版本已被提議作為暗物質的候選者。 ^{[30] [31]}還有人提出，如果在大爆炸前後出現了一個由負質量宇宙弦保持開放的微小蟲洞，那麼它可能會在宇宙膨脹的作用下膨脹到宏觀尺寸。 ^[32]

模擬可穿越蟲洞的圖像，連接圖賓根大學物理研究所前的廣場和法國北部濱海布洛涅附近的沙丘。該圖像是使用 Morris-Thorne 蟲洞度量中的 4D光線追蹤計算得出的，但尚未模擬重力對光波長的影響。 ^{[註 1]}

勞侖茲可穿越蟲洞可以讓人非常快速地從宇宙的一部分旅行到同一宇宙的另一部分，或者從一個宇宙旅行到另一個宇宙。廣義相對論中可穿越蟲洞的可能性最早由 Homer Ellis 在 1973 年的一篇論文中證明^[33] ，隨後 K.A. Bronnikov 在同年發表的一篇論文中獨立證明了這^[34] 。埃利斯分析了埃利斯排水孔的拓撲結構和測地線，表明它是測地線完整的、無水平面的、無奇異點的，並且在兩個方向上完全可穿越。排水孔是愛因斯坦真空時空場方程式的解流形，通過包含與具有反正統極性（負而不是正）的里奇張量最小耦合的純量場進行了修改。 （埃利斯特別拒絕將純量場稱為「奇異的」，因為它具有反正統的耦合性，他認為這樣做的論據缺乏說服力。）該解決方案取決於兩個參數： m ，它決定了其重力場的強度，以及n ，它決定了其空間橫截面的曲率。當m設置為等於 0 時，排水孔的重力場消失。剩下的就是埃利斯蟲洞，一種非重力、純幾何、可穿越的蟲洞。

1988 年，基普·索恩和他的研究生邁克·莫里斯分別發現了埃利斯蟲洞，並主張將其作為教授廣義相對論的工具。 ^[35]因此，他們提出的這種由奇異物質球殼支撐的可穿越蟲洞也被稱為莫里斯-索恩蟲洞。

後來，其他類型的可穿越蟲洞被發現是廣義相對論方程式的可解，其中包括馬特·維瑟 (Matt Visser) 在 1989 年的一篇論文中分析的一種，其中可以製作一條穿過蟲洞的路徑，而穿越路徑不會經過奇異物質區域。然而，在純高斯-博內重力（廣義相對論的一種修正，涉及額外空間維度，有時會在膜宇宙學的背景下進行研究）中，蟲洞的存在並不需要奇異物質 —— 甚至在沒有物質的情況下它們也可以存在。 ^[36]維瑟與克雷默等人合作提出了一種由負質量宇宙弦保持開放的類型， ^[32]他們認為這種蟲洞可以在早期宇宙中自然形成。

蟲洞連接時空中的兩點，這意味着原則上它們可以實現時間旅行，也可以實現空間旅行。 1988年，莫里斯（Morris）、索恩（Thorne）和尤爾特塞弗（Yurtsever）研究出如何通過加速蟲洞的兩個入口之一，將穿越空間的蟲洞轉換為穿越時間的蟲洞。 ^[23]然而，根據廣義相對論，不可能利用蟲洞回到早於蟲洞首次被轉換成時間「機器」的時間。在此之前，它不可能被注意到或被利用。 ^{[28] :504}

宇宙間的旅行

解決蟲洞時間旅行悖論的一個可能方法依賴於量子力學的多重世界詮釋。

1991 年，大衛·多伊奇（David Deutsch）證明，量子理論在具有封閉類時曲線的時空中是完全一致的（即所謂的密度矩陣可以不受不連續性的影響）。 ^[37]後來，人們發現，這種封閉類時曲線模型可能存在內部不一致性，因為它會導致一些奇怪的現象，比如區分非正交量子態，區分適當混合和非適當混合。 ^{[38] [39]}因此，半經典計算表明的虛擬粒子在蟲洞時間機器中循環的破壞性正反饋迴路被避免了。從未來返回的粒子不會返回其起源的宇宙，而是返回平行宇宙。這表明，具有極短時間跳躍的蟲洞時間機器是同時存在的平行宇宙之間的理論橋樑。 ^[9]

因為蟲洞時間機器在量子理論中引入了一種非線性，所以這種平行宇宙之間的通信與約瑟夫·波爾欽斯基在史蒂文·溫伯格的非線性量子力學表述中提出的埃弗雷特電話^[40] （以休·埃弗雷特的名字命名）的提議一致。

平行宇宙之間進行通訊的可能性被稱為宇宙間旅行。

蟲洞也可以用史瓦西黑洞的潘洛斯圖來描繪。在潘洛斯圖中，一個運動速度超光速的物體將穿過黑洞，從另一端進入不同的空間、時間或宇宙。這將是一個宇宙間的蟲洞。

度規

「蟲洞度規」描述了蟲洞的時空幾何，並作為時間旅行的理論模型。一個（可穿越的）蟲洞度規的例子如下：^[41]

${\displaystyle ds^{2}=-c^{2}\,dt^{2}+d\ell ^{2}+(k^{2}+\ell ^{2})(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}),}$

由埃利斯首次提出，此為埃利斯排水孔（英語：Ellis drainhole）的特例

一種不可穿越的蟲洞的度規是史瓦西解（見第一張圖）：

${\displaystyle ds^{2}=-c^{2}\left(1-{\frac {2GM}{rc^{2}}}\right)\,dt^{2}+{\frac {dr^{2}}{1-{\frac {2GM}{rc^{2}}}}}+r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}).}$

1935年7月發表的一篇文章描述了最初的愛因斯坦-羅森橋。^[42][43]

對於史瓦西球對稱靜態解：

${\displaystyle ds^{2}=-{\frac {1}{1-{\frac {2m}{r}}}}\,dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+\left(1-{\frac {2m}{r}}\right)\,dt^{2},}$

在這裏${\displaystyle ds}$是原時而光速${\displaystyle c=1}$

利用${\displaystyle u^{2}=r-2m}$，把${\displaystyle r}$換成${\displaystyle u}$

${\displaystyle ds^{2}=-4(u^{2}+2m)\,du^{2}-(u^{2}+2m)^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+{\frac {u^{2}}{u^{2}+2m}}\,dt^{2}}$

數學上將這個解的四維時空想成兩個全等部分，或是兩片紙片，根據 ${\displaystyle u>0}$ 或 ${\displaystyle u<0}$決定這個點在哪片時空部分上。這兩個時空部分被${\displaystyle r=2m}$ （即 ${\displaystyle u=0}$）這個超曲面連接。我們稱這樣的連接是個「橋」

——愛因斯坦、羅森：「廣義相對論中的粒子問題」

考慮到重力場以及電場，愛因斯坦和羅森推導出以下史瓦西靜態球對稱解

${\displaystyle \varphi _{1}=\varphi _{2}=\varphi _{3}=0,\varphi _{4}={\frac {\varepsilon }{4}},}$

${\displaystyle ds^{2}=-{\frac {1}{\left(1-{\frac {2m}{r}}-{\frac {\varepsilon ^{2}}{2r^{2}}}\right)}}\,dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+\left(1-{\frac {2m}{r}}-{\frac {\varepsilon ^{2}}{2r^{2}}}\right)\,dt^{2},}$

${\displaystyle \varepsilon }$ 代表電荷

沒有分母的場方程式（在${\displaystyle m=0}$的情況下）可寫為

${\displaystyle \varphi _{\mu \nu }=\varphi _{\mu ,\nu }-\varphi _{\nu ,\mu }}$

${\displaystyle g^{2}\varphi _{\mu \nu ;\sigma }g^{\nu \sigma }=0}$

${\displaystyle g^{2}(R_{ik}+\varphi _{i\alpha }\varphi _{k}^{\alpha }-{\frac {1}{4}}g_{ik}\varphi _{\alpha \beta }\varphi ^{\alpha \beta })=0}$

為了去除奇異點，若把${\displaystyle r}$換為${\displaystyle u}$根據：

${\displaystyle u^{2}=r^{2}-{\frac {\varepsilon ^{2}}{2}}}$

又${\displaystyle m=0}$，可得^[44][45]

${\displaystyle \varphi _{1}=\varphi _{2}=\varphi _{3}=0}$ and ${\displaystyle \varphi _{4}={\frac {\varepsilon }{\left(u^{2}+{\frac {\varepsilon ^{2}}{2}}\right)^{1/2}}}}$

${\displaystyle ds^{2}=-du^{2}-\left(u^{2}+{\frac {\varepsilon ^{2}}{2}}\right)(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+\left({\frac {2u^{2}}{2u^{2}+\varepsilon ^{2}}}\right)\,dt^{2}}$

在這個解中，對於兩張紙空間中的所有有限點，解都沒有奇異點

——愛因斯坦，羅森：「廣義相對論中的粒子問題」

流行文化

• 蟲洞是科幻小說中的常見元素，因為它們允許星際、星系間，有時甚至是人類生命尺度內的宇宙間旅行。在小說中，蟲洞也被用作時間旅行的一種方法。

• 2014年科幻電影《星際效應》

參考資料