热门问题
时间线
聊天
视角
圓
同一平面上,到定點的距離等於定長的所有點的集合 来自维基百科,自由的百科全书
Remove ads
圓 (英語:circle, round)的第一個定義是:根據歐幾里得的《幾何原本》,在同一平面內到定點 的距離等於定長 的點的集合[1]。此定點 稱為圓心(center of a circle),此定長 稱為半徑(radius)。
圓的第二個定義是:平面內一動點到兩定點的距離的比,等於一個不為1的常數,則此動點的軌跡是圓[2];此圓屬於一種阿波羅尼奧斯圓(circles of Apollonius)。
Remove ads
歷史
古代人最早是從太陽、陰曆十五的月亮得到圓的概念的。在一萬八千年前的山頂洞人曾經在獸牙、礫石和石珠上鑽孔,那些孔有的就很像圓。[3]到了陶器時代,許多陶器都是圓的。圓的陶器是將泥土放在一個轉盤上製成的。[4]當人們開始紡線,又制出了圓形的石紡錘或陶紡錘。古代人還發現搬運圓的木頭時滾着走比較省勁。後來他們在搬運重物的時候,就把幾段圓木墊在大樹、大石頭下面滾着走。[5]
約在6000年前,美索不達米亞人,做出了世界上第一個輪子——圓型的木盤。[4]大約在4000多年前,人們將圓的木盤固定在木架下,這就成了最初的車子。 古代埃及人認為:圓,是神賜給人的神聖圖形。一直到兩千多年前中國的墨子給圓下了一個定義:圓,一中同長也。意思是說:圓有一個圓心,圓心到圓周上各點的距離(即半徑)都相等。[4]
性質
圓是在同一平面內到定點的距離等於定長的點的集合,這個定點叫做圓的圓心(通常用表示)。[6]
Remove ads
假如一條直線與圓相交僅有一個交點,那麼稱這條直線是這個圓的切線,與圓相交的點叫做切點。[2]如下圖,直線與圓只有一個交點,那麼就是圓的切線。過圓上一點的切線:設該點為,圓的方程為,則圓在該點的切線方程為:
Remove ads
一條直線與一條弧線有兩個公共點,這條直線是這條曲線的割線(英語:Secant Theorem)。[2]如圖,直線與圓有兩個公共點,那麼直線就是圓的割線。

圓的一周的長度稱為圓的周長(記作)。圓的周長與半徑的關係是:
- 或 ,
其中是圓周率。
圓的面積與半徑的關係是:。
圓心角、圓周角

圓周角定理:同弧所對的圓周角等於它所對的圓心的角的一半。[6]
如上圖,為圓心,分別為圓周上的點,那麼:
- 證明:
- 即:
圓周角定理的推論:
垂徑定理

一條直線,在下列5條中只要具備其中任意兩條作為條件,就可以推出其他三條結論。稱為「知二推三」。
- 平分弦所對的優弧
- 平分弦所對的劣弧(前兩條合起來就是平分弦所對的兩條弧)
- 平分弦(不是直徑)
- 垂直於弦
- 經過圓心
兩圓位置關係
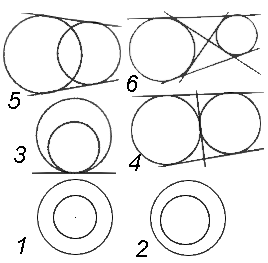
兩個不同大小的圓(半徑分別為及,圓心距為,其中)之間的關係如下:[2]
- :兩圓不相交(內含),互為同心圓。
- :兩圓不相交(內含,亦稱「內離」)。
- :兩圓相交於一點(內切),有1條共同切線。
- :兩圓相交於一點(外切),有3條共同切線。
- :兩圓相交於兩點,有2條共同切線。
- :兩圓不相交(外離),有4條共同切線。
在解析幾何中,符合特定條件的某些圓構成一個圓系,一個圓系所具有的共同形式的方程稱為圓系方程。例如求半逕到直線距離的方程就可以叫圓系方程。[2]
在方程中,若圓心為定點,為參變數,則它表示同心圓的圓系方程。若是常量,(或)為參變數,則它表示半徑相同,圓心在同一直線上(平行於軸或軸)的圓系方程。
- 過兩圓與交點的圓系方程為:
- 過直線與圓交點的圓系方程為:
- 過兩圓與交點的直線方程為:
其他定義
其它
參考資料
參見
擴展閱讀
外部連結
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads











































































