雙極坐標系

二維雙極坐標系（英語：Bipolar coordinates）是一個正交坐標系。學術界上有三種常用的雙極坐標系^[1]。除了在這裏討論的坐標系以外，另外兩種是非正交的雙心坐標系與雙角坐標系。

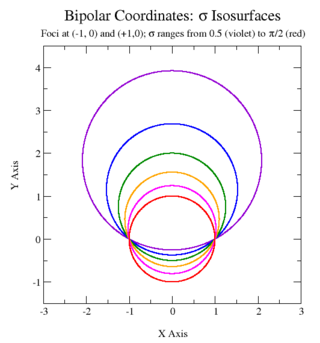
雙極坐標系繪圖。圖中的紅色圓圈是 ${\displaystyle \sigma \,\!}$-等值曲線，藍色圓圈則是 ${\displaystyle \tau \,\!}$-等值曲線。

這裡所要討論的雙極坐標系建立於阿波羅尼奧斯圓。${\displaystyle \sigma \,\!}$ 的等值曲線是圓圈。 ${\displaystyle \tau \,\!}$ 的等值曲線也是圓圈。兩組圓圈互相垂直相交。雙極坐標系有兩個焦點 ${\displaystyle F_{1}\,\!}$ 與 ${\displaystyle F_{2}\,\!}$ ，其直角坐標 ${\displaystyle (x,\ y)\,\!}$ 通常分別設定為 ${\displaystyle (-a,\ 0)\,\!}$ 與 ${\displaystyle (a,\ 0)\,\!}$ 。所以，這兩個焦點都處於直角坐標系的 x-軸。

雙極坐標系是好幾種三維正交坐標系的原始模。往 z-軸方向延伸，則可得到雙極圓柱坐標系。繞著 x-軸旋轉，即可得到雙球坐標系。繞著 y-軸旋轉，就可得到圓環坐標系。

基本定義

雙極坐標的幾何詮釋。 ${\displaystyle {\overline {F_{1}P}}\,\!}$ 與 ${\displaystyle {\overline {F_{2}P}}\,\!}$ 的夾角 ${\displaystyle \angle F_{1}PF_{2}\,\!}$ 的弧度是 ${\displaystyle \sigma \,\!}$ 。${\displaystyle F_{1}P\,\!}$ 與 ${\displaystyle F_{2}P\,\!}$ 的比例的自然對數是 ${\displaystyle \tau \,\!}$ 。${\displaystyle \sigma \,\!}$ 與 ${\displaystyle \tau \,\!}$ 的等值曲線都是圓圈，分別以紅色與藍色表示。兩條等值曲線以直角相交（以洋紅色表示）。

在二維空間裏，一個點 P 的雙極坐標 ${\displaystyle (\sigma ,\ \tau )\,\!}$ 通常定義為

${\displaystyle x=a\ {\frac {\sinh \tau }{\cosh \tau -\cos \sigma }}\,\!}$，

${\displaystyle y=a\ {\frac {\sin \sigma }{\cosh \tau -\cos \sigma }}\,\!}$；

其中，點 ${\displaystyle P\,\!}$ 的 ${\displaystyle \sigma \,\!}$ 坐標等於 ${\displaystyle \angle F_{1}PF_{2}\,\!}$ 的弧度，${\displaystyle \tau \,\!}$ 坐標等於 ${\displaystyle d_{1}=F_{1}P\,\!}$ 與 ${\displaystyle d_{2}=F_{2}P\,\!}$ 的比例的自然對數

${\displaystyle \tau =\ln {\frac {d_{1}}{d_{2}}}\,\!}$。

（回想 ${\displaystyle F_{1}\,\!}$ 與 ${\displaystyle F_{2}\,\!}$ 的坐標分別為 ${\displaystyle (-a,\ 0)\,\!}$ 與 ${\displaystyle (a,\ 0)\,\!}$ ）。

等值曲線

不同 ${\displaystyle \sigma \,\!}$ 的等值曲線是一組不同圓心，而相交於兩個焦點 ${\displaystyle F_{1}\,\!}$ 與 ${\displaystyle F_{2}\,\!}$ 的圓圈：

${\displaystyle x^{2}+(y-a\cot \sigma )^{2}={\frac {a^{2}}{\sin ^{2}\sigma }}\,\!}$

它們的圓心都包含於 y-軸。正值 ${\displaystyle \sigma \,\!}$ 的圓圈的圓心都在 x-軸以上；而負值 ${\displaystyle \sigma \,\!}$ 的圓圈的圓心則在 x-軸以下。當絕對值 ${\displaystyle \left|\sigma \right|\,\!}$ 增加時，圓半徑會減小，圓心會靠近原點。當圓心與原點同點時，${\displaystyle \left|\sigma \right|\,\!}$ 達到最大值 ${\displaystyle \pi /2\,\!}$ 。

不同 ${\displaystyle \tau \,\!}$ 的等值曲線是一組圍著焦點，互不相交，不同半徑的圓圈。半徑為

${\displaystyle y^{2}+\left(x-a\coth \tau \right)^{2}={\frac {a^{2}}{\sinh ^{2}\tau }}\,\!}$ 。

它們的圓心都包含於 x-軸。正值 ${\displaystyle \tau \,\!}$ 的圓圈在 ${\displaystyle x>0\,\!}$ 半平面；而負值 ${\displaystyle \tau \,\!}$ 的圓圈在 ${\displaystyle x<0\,\!}$ 半平面。${\displaystyle \tau =0\,\!}$ 曲線則與 y-軸同軸。當 ${\displaystyle \tau \,\!}$ 值增加時，圓圈的半徑會減少，圓心會靠近焦點。

逆變換

雙極坐標 ${\displaystyle (\sigma ,\ \tau )\,\!}$ 可以用直角坐標 ${\displaystyle (x,\ y)\,\!}$ 來表達。點 P 與兩個焦點之間的距離是

${\displaystyle d_{1}^{2}=(x+a)^{2}+y^{2}\,\!}$ ，

${\displaystyle d_{2}^{2}=(x-a)^{2}+y^{2}\,\!}$ 。

${\displaystyle \tau \,\!}$ 是 ${\displaystyle d_{1}\,\!}$ 與 ${\displaystyle d_{2}\,\!}$ 的比例的自然對數：

${\displaystyle \tau =\ln {\frac {d_{1}}{d_{2}}}\,\!}$ 。

${\displaystyle \angle F_{1}PF_{2}\,\!}$ 是兩條從點 P 到兩個焦點的線段 ${\displaystyle {\overline {F_{1}P}}\,\!}$ 與 ${\displaystyle {\overline {F_{2}P}}\,\!}$ 的夾角。這夾角的弧度是 ${\displaystyle \sigma \,\!}$ 。用餘弦定理來計算：

${\displaystyle \cos \sigma ={\frac {d_{1}^{2}+d_{2}^{2}-4a^{2}}{2d_{1}d_{2}}}\,\!}$ ；

標度因子

雙極坐標 ${\displaystyle (\sigma ,\ \tau )\,\!}$ 的標度因子相等：

${\displaystyle h_{\sigma }=h_{\tau }={\frac {a}{\cosh \tau -\cos \sigma }}\,\!}$ 。

所以，無窮小面積元素等於

${\displaystyle dA={\frac {a^{2}}{(\cosh \tau -\cos \sigma )^{2}}}\ d\sigma d\tau \,\!}$ 。

拉普拉斯算子是

${\displaystyle \nabla ^{2}\Phi =\left({\frac {\cosh \tau -\cos \sigma }{a}}\right)^{2}({\frac {\partial ^{2}\Phi }{\partial \sigma ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \tau ^{2}}})\,\!}$ 。

其它微分算子，例如 ${\displaystyle \nabla \cdot \mathbf {F} \,\!}$ 與 ${\displaystyle \nabla \times \mathbf {F} \,\!}$ ，都可以用雙極坐標表達，只需要將標度因子代入正交坐標系的一般方程式內。

應用

雙極坐標有一個經典的應用是在解析像拉普拉斯方程或亥姆霍茲方程這類的偏微分方程式。在這些方程式裏，雙極坐標允許分離變數法的使用。一個典型的例題是，「有兩個互相平行的圓柱導體，請問其周圍的電場為什麼？」 應用雙極坐標，我們可以精緻地分析這例題。

參閱

• 拉普拉斯-龍格-冷次向量

參考文獻

• H. Bateman "Spheroidal and bipolar coordinates", Duke Mathematical Journal 4 (1938), no. 1, 39–50。
• Lockwood, E. H. "Bipolar Coordinates." Chapter 25 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 186-190, 1967。
• Korn GA and Korn TM, (1961) Mathematical Handbook for Scientists and Engineers, McGraw-Hill。

1. Weisstein, Eric W. (編). 雙極坐標系. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2008-04-21]. （原始內容存檔於2021-05-20） （英語）.