五邊形鑲嵌

在幾何學中，五邊形鑲嵌是指用五邊形鑲嵌平面。

已知的15種凸五邊形鑲嵌

正五邊形不能鑲嵌平面，因為其內角是108°，不能整除360°。截至2015年 (2015-Missing required parameter 1=month!)^[update]，已知有15種凸五邊形鑲嵌平面。2017年5月，里昂高等師範學校Michaël Rao宣稱已證明只存在上述的15種凸五邊形鑲嵌平面情況。^[1]

歷史

Reinhardt (1918)發現了「鑲嵌塊遞移」（tile transitive）的5種五邊形鑲嵌，即是說鑲嵌的對稱性可以將任何一塊帶到任何另一塊（用數學語言描述，鑲嵌的自同構群作用在鑲嵌塊上是可遞的。）Kershner (1968)發現了3種新的五邊形鑲嵌，都不是鑲嵌遞移的；他錯誤聲稱已經找出所有的五邊形鑲嵌。1975年Richard E. James III找到第9種。Schattschneider (1978)描述業餘數學家瑪喬里·賴斯在1976至1977年間找到新的4種五邊形鑲嵌。Schattschneider (1985)描述Rolf Stein在1985年找到的第14種五邊形鑲嵌。Bagina (2011)證明邊對邊（edge-to-edge）的凸五邊形鑲嵌只有8種，Sugimoto (2012)獨立證出同一結果。2015年，華盛頓大學數學家Casey Mann、Jennifer McLoud和David Von Derau發現了第15種五邊形鑲嵌，使用了電腦算法搜尋。^[2]

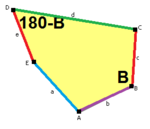
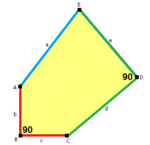
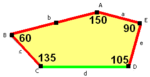
五邊形的性質

15種凸五邊形鑲嵌平面

1	2	3	4	5
B+C=180° A+D+E=360°	c=e B+D=180°	a = b, d = c + e A = C = D = 120°	b = c, d = e B = D = 90°	a = b, d = e A = 60°, D = 120°
6	7	8	9	10
a = d = e, b = c B + D = 180°, 2B = E	b = c = d = e B + 2E = 2C + D = 360°	b = c = d = e 2B + C = D + 2E = 360°	b = c = d = e 2A + C = D + 2E = 360°	a = b = c + e A = 90°, B + E = 180°, B + 2C = 360°
11	12	13	14	15
2a + c = d = e A = 90°, 2B + C = 360° C + E = 180°	2a = d = c + e A = 90°, 2B + C = 360° C + E = 180°	d = 2a = 2e B = E = 90°, 2A + D = 360°	2a = 2c = d = e A = 90°, B ≈ 145.34°, C ≈ 69.32°, D ≈ 124.66°, E ≈ 110.68° (2B + C = 360°, C + E = 180°).	a = c = e, b = 2a A = 150°, B = 60°, C = 135°, D = 105°, E = 90°

參考文獻

引用

1. Exhaustive search of convex pentagons which tile the plane (PDF). [2017-07-19]. （原始內容存檔 (PDF)於2020-11-12）.
2. Bellos, Alex. Attack on the pentagon results in discovery of new mathematical tile. The Guardian. 11 August 2015 [2015-08-18]. （原始內容存檔於2015-08-18）.

引用錯誤：在<references>標籤中name屬性為「NPR」的參考文獻沒有在文中使用

來源

• Bagina, Olga, Tiling the plane with congruent equilateral convex pentagons, Journal of Combinatorial Theory. Series A, 2004, 105 (2): 221–232, ISSN 1096-0899, MR 2046081, doi:10.1016/j.jcta.2003.11.002
• Bagina, Olga, Мозаики из выпуклых пятиугольников [Tilings of the plane with convex pentagons], Vestnik (Kemerovo State University), 2011, 4 (48): 63–73 [29 January 2013], ISSN 2078-1768, （原始內容存檔於2015-10-01） （俄語）
• Grünbaum, Branko; Shephard, Geoffrey C., Tilings by polygons, Tilings and Patterns, New York: W. H. Freeman and Company, 1987, ISBN 0-7167-1193-1, MR 0857454
• Gardner, Martin, Tiling with Convex Polygons, Time travel and other mathematical bewilderments, New York: W. H. Freeman and Company, 1988, ISBN 0-7167-1925-8, MR 0905872
• Godrèche, C., The sphinx: a limit-periodic tiling of the plane, Journal of Physics A: Mathematical and General, 1989, 22 (24): L1163–L1166, MR 1030678, doi:10.1088/0305-4470/22/24/006
• Hirschhorn, M. D.; Hunt, D. C., Equilateral convex pentagons which tile the plane, Journal of Combinatorial Theory. Series A, 1985, 39 (1): 1–18, ISSN 1096-0899, MR 0787713, doi:10.1016/0097-3165(85)90078-0
• Kershner, Richard, On paving the plane, American Mathematical Monthly, 1968, 75: 839–844 [2015-08-18], ISSN 0002-9890, MR 0236822, doi:10.2307/2314332, （原始內容存檔於2016-03-05）
• Reinhardt, Karl, Über die Zerlegung der Ebene in Polygone, Dissertation Frankfurt a.M., Borna-Leipzig, Druck von Robert Noske, 1918 （德語）
• Schattschneider, Doris, Tiling the plane with congruent pentagons, Mathematics Magazine, 1978, 51 (1): 29–44 [2015-08-18], ISSN 0025-570X, MR 0493766, doi:10.2307/2689644, （原始內容存檔於2015-08-18）
• Schattschneider, Doris, A new pentagon tiler, Mathematics Magazine, 1985, 58 (5): 308, The cover has a picture of the new tiling
• Sugimoto, Teruhisa, Convex pentagons for edge-to-edge tiling, I. (PDF), Forma, 2012, 27 (1): 93–103 [2015-08-18], MR 3030316, （原始內容存檔 (PDF)於2015-09-24）

外部連結

• 埃里克·韋斯坦因. Pentagon Tiling. MathWorld.
• Pentagon Tilings（頁面存檔備份，存於網際網路檔案館）
• The 14 Pentagons that Tile the Plane（頁面存檔備份，存於網際網路檔案館）

參見

• 數學主題

• 五邊形