槓桿
由以固定中心或支點為樞軸的樑或剛性桿組成的簡單機器 来自维基百科,自由的百科全书
在力學裡,典型的槓桿是置放連結在一個支撐點上的硬棒,這硬棒可以繞著支撐點旋轉。當槓桿靜力平衡時,其施力乘以施力臂等於抗力乘以抗力臂,可以透過改變施力臂或抗力臂長度,使輸入力放大或縮小,有著相當實用的功能,古希臘人將槓桿歸類為簡單機械。[1]
| 槓桿 | |
|---|---|
 遵守槓桿原理,置放在槓桿上的兩個重物呈靜力平衡狀態。 | |
| 分類 | 簡單機械 |
歷史

早在舊石器時代晚期,古人就知道使用槓桿的原理來製作投槍器。 [2] 考古學者認為,在古埃及4500多年前的金字塔時期,工人使用槓桿來移動、抬舉重量超過100英噸的方尖碑。[3] 中國戰國時期,墨子在所著作的《墨子》一書中,提到應用槓桿的概念。[註 1][4][5]
大約在西元前330年,亞里斯多德在著作《機械問題》(《Mechanical Problems》)裏,對於槓桿有詳細的論述,並且基本而言使用虛功的現代概念推導出槓桿原理。[6]西元前3世紀,古希臘科學家阿基米德在著作《論平面圖形的平衡》裏用幾何方法推導出槓桿原理,[7]並且宣稱:「給我一個支點,我就可以撬動整個地球。」[註 2][8]
概述
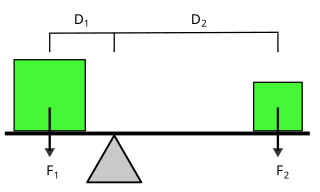
由於槓桿內部有一點為固定點,槓桿只能繞著這固定點做旋轉運動。相對於這一點,槓桿不能做平移運動。
- 槓桿內部的固定點稱為「支點」。
- 使槓桿旋轉的力 叫做「施力」,是輸入力。
- 施力作用於槓桿的位置叫做「施力點」。
- 阻礙槓桿旋轉的力 叫做「抗力」,是輸出力。
- 抗力作用於槓桿的位置叫做「抗力點」。
- 從支點到施力作用線的垂直距離 叫做「施力臂」。
- 從支點到抗力作用線的垂直距離 叫做「抗力臂」。
理想槓桿不會耗散或儲存能量,也就是說,支點與硬棒之間不會出現任何摩擦損耗,硬棒是一種剛體,不會被彎曲,發生形變。注意到硬棒不一定是直棒。彎曲的硬棒形成的槓桿稱為「曲槓桿」。對於理想槓桿案例,輸入槓桿的功率等於槓桿輸出的功率。輸出力與輸入力之間的比率,等於這兩個作用力分別與支點之間垂直距離的反比率,稱這相等式為「槓桿原理」,以方程式表達:
- ,
或者,
- 。
定義力矩 為
- ;
其中, 是作用力, 是作用力與支點之間的垂直距離。
- 。
槓桿原理表明,當靜力平衡時,施力乘以施力臂等於抗力乘以抗力臂:
- 。
槓桿的分類
靠著比較施力臂、抗力臂的長度,可以將槓桿分為三類:
- 施力臂長於抗力臂的槓桿是「省力槓桿」,這可以省力。開瓶器、撬棍等均為省力槓桿。
- 抗力臂長於施力臂的是「費力槓桿」,這可以省時。大部分剪刀、鑷子、筷子、釣魚竿、火鉗、筆等均為費力槓桿。
- 施力臂和抗力臂長度相等的槓桿是「等臂槓桿」,蹺蹺板、天秤等均為等臂槓桿。
另外一種分類法式依照施力點、抗力點、支點在槓桿的相對位置來分類。[9]


第二類槓桿的施力點、支點分別在抗力點的兩邊。例如,獨輪車、胡桃鉗、開瓶器。這是一種省力槓桿,可以施加較小的力量來移動較重的物體,但是施力的位移較長.

槓桿原理
槓桿是可以繞著支點旋轉的硬棒。當外力作用於槓桿內部任意位置時,槓桿的響應是其操作機制;假若外力的作用點是支點,則槓桿不會出現任何響應。
假設槓桿不會耗散或儲存能量,則槓桿的輸入功率必等於輸出功率。當槓桿繞著支點呈勻角速度旋轉運動時,離支點越遠,則移動速度越快,離支點越近,則移動速度越慢,由於功率等於作用力乘以速度,離支點越遠,則作用力越小,離支點越近,則作用力越大。

機械利益是抗力與施力之間的比率,或輸出力與輸入力之間的比率。假設施力臂 、抗力臂 分別為施力點、抗力點與支點之間的距離,施力 、抗力 分別作用於施力點、抗力點。則機械利益 為
- 。
通常在學習槓桿的初級理論時,會聚焦於輸入力和輸出力由於虛位移而做的虛功。虛位移可以定義為物體的移動速度乘以虛時間。這樣定義導致計算的物理量是功率,而不是功。這種方法有一個實在優點:在研究機械工程學或機構學時,功率是主要計算的物理量。使用這種方法來對槓桿做靜力分析,就如同對於車子的傳動系統,或機械手臂做靜力分析,它們的機械利益的計算方式完全一樣。
複式槓桿

複式槓桿是一組耦合在一起的槓桿,前一個槓桿的抗力會緊接地成為後一個槓桿的施力。幾乎所有的磅秤都會應用到某種複式槓桿機制。其它常見例子包括指甲剪、鋼琴鍵盤。1743年,英國伯明罕發明家約翰·外艾特在設計計重秤時,貢獻出複式槓桿的點子。他設計的計重秤一共使用了四個槓桿來傳輸負載。[10]
參閱
注釋
參考文獻
外部連結
Wikiwand - on
Seamless Wikipedia browsing. On steroids.













