角

在幾何學中，角（ㄐㄧㄠˇ）（英語：angle）或精確用語平面角，是由兩條有公共端點的射線組成的幾何對象。這兩條射線叫做角的邊，它們的公共端點叫做角的頂點。一般的角會假設在歐幾里得平面上，但在非歐幾里得幾何中也可以定義角，特別是在球面幾何學中的球面角（英語：spherical angle）是用大圓的圓弧代替射線。角在幾何學和三角學中有着廣泛的應用。

此條目頁的主題是數學名詞角。關於與「角」標題相近或相同的條目頁，請見「角 (消歧義)」。

Unicode中的角符號，碼位為U+2220

幾何之父歐幾里得曾定義角為在平面中兩條不平行的直線的相對斜度。普羅克魯斯認為角可能是一種特質、一種可量化的量、或是一種關係。歐德謨（英語：Eudemus）認為角是相對一直線的偏差，安提阿的卡布斯（英語：Carpus of Antioch）認為角是二條相交直線之間的空間。歐幾里得認為角是一種關係，不過他對直角、銳角或鈍角的定義都是量化的^[1]。

平面角大小的計量單位制常用的有360度制、弧度制等^[2][3]。

表示方法

角通常用三個字母表示：兩條邊上的點的字母寫在兩旁，頂點上的字母寫在中間。圖中的角用∠AOB或${\displaystyle {\widehat {AOB}}}$表示。但若在不會產生混淆的情形下，也會直接用頂點的字母表示，例如角∠O。

在數學式中，一般會用希臘字母（${\displaystyle \alpha ,\beta ,\gamma ,\theta ,\varphi ,...}$）表示角的大小。為避免混淆，符號π一般不用來表示角度。

角的測量

常見測量單位

以角的端點為圓心做圓弧。由於圓弧的半徑和弧長成正比，而角是長度的比例，所以圓的大小不會影響角的測量。

• 角度：由角在圓上所切出的圓弧的長度除以圓的周長再乘以360的結果，一般用°來標記，讀作「度」。一度可以繼續分為60「分」或3600「秒」。角度在天文學和全球定位系統中有重要應用。

• 弧度：用角在圓上所切出的圓弧的長度除以圓的半徑，單位是rad（中文名：弳）。弧度在數學中有廣泛的應用。弧度還是國際單位制中規定的角的標準度量，但卻不是中國法定計量單位，角度則是角在中國的法定計量單位。

採用弧度時，通常不會標示單位，例如：${\displaystyle \sin \pi =\sin 180^{\circ }=0}$

• 百分度：是角在圓上所切出的圓弧的長度除以圓的周長再乘以400的結果。

其他測量單位

角度的量測可以視為弧長s和半徑r的比例，再依選用單位乘以一比例係數${\displaystyle {\frac {2\pi }{n}}}$。

${\displaystyle \theta ={\frac {n}{2\pi }}{\frac {s}{r}}}$

例如以上的弧度、角度和百分度，其轉換係數${\displaystyle n}$分別為${\displaystyle 2\pi }$、360和400。

以下是一些其他的測量單位，對應不同的${\displaystyle n}$值。

• 圈數或轉數（${\displaystyle n=1}$）：是指完整旋轉一圈，依應用的不同，會簡寫為cyc、rev或rot，不過在每分鐘轉速（RPM）的單位中，只用一個字母r表示。
• 直角（${\displaystyle n=4}$）：是${\displaystyle {\frac {1}{4}}}$圈，是幾何原本中用的角度單位，直角${\displaystyle =90^{\circ }={\frac {\pi }{2}}\mathrm {rad} ={\frac {1}{4}}\mathrm {turn} =100\mathrm {grad} }$。在德文中曾用${\displaystyle \llcorner }$表示直角。
• 時角（${\displaystyle n=24}$）：）常用在天文學中，是${\displaystyle {\frac {1}{24}}}$圈。此系統是用在一天一個週期的循環（例如星星的相對位置），其六十進制下的子單位稱為「時間分角」及「時間秒角」，這兩個單位和角度的角分及角秒不同，前者大小為後者的十五倍。1時角${\displaystyle =15^{\circ }={\frac {\pi }{12}}\mathrm {rad} ={\frac {1}{6}}\mathrm {quad} ={\frac {1}{24}}\mathrm {turn} \approx 16.667\mathrm {grad} }$。
• 密位（${\displaystyle n=6000\sim 6400}$）：此單位是指一個單位大約等於毫弧度的角度，有許多不同的定義，其數值從0.05625度到0.06度（3.375至3.6角分），而毫弧度約為0.05729578度（3.43775角分）。在北大西洋公約組織的國家中，密位定義為圓的${\displaystyle {\frac {1}{6400}}}$。其數值大約等於一個角度的弧長為一公尺，其半徑為一公里的角度（${\displaystyle {\frac {2\pi }{6400}}=0.0009817...\doteqdot {\frac {1}{1000}}}$）。瑞典歷史上以圓周爲6300密位（最接近），但在2007年同北約一致。
• 角分（${\displaystyle n=21600}$）：定義為一度的${\displaystyle {\frac {1}{60}}}$，是${\displaystyle {\frac {1}{21600}}}$圈，會用 ′ 表示，例如3° 30′ 等於${\displaystyle 3+{\frac {30}{60}}}$度，也就是3.5度，有時也會出現小數，例如${\displaystyle 3^{\circ }5.72'=3+{\frac {5.72}{60}}}$度。海里曾定義為在地球的大圓上一角分的弧長。
• 角秒 （${\displaystyle n=1296000}$）：定義為一角分的${\displaystyle {\frac {1}{60}}}$，會用 ″ 表示，例如3° 7′ 30″等於${\displaystyle 3+{\frac {7}{60}}+{\frac {30}{3600}}}$度，或是3.125 度。

正角和負角

以上角的定義均未考慮數值為負的角。不過在一些應用時，會將角的數值加上正負號，以標明是相對參考物不同方向的旋轉。

在二維的笛卡兒坐標系中，角一般是以x軸的正向為基準，若往y軸的正向旋轉，則其角為正角，若往y軸的負向旋轉，則其角為負角。若二維的笛卡兒坐標系也是x軸朝右，y軸朝上，則逆時針的旋轉對應正角，順時針的旋轉對應負角。

一般而言，${\displaystyle -\theta }$角和一圈減去${\displaystyle \theta }$所得的角等效。例如${\displaystyle -45^{\circ }}$和${\displaystyle 360^{\circ }-45^{\circ }(=315^{\circ })}$等效，但這只適用在用角表示相對位置，不是旋轉概念時。旋轉${\displaystyle -45^{\circ }}$和旋轉315°是不同的。

在三維的幾何中，順時針及逆時針沒有絕對的定義，因此定義正角及負角時均需列出其參考的基準，一般會以一個通過角的頂點，和角所在平面垂直的向量為基準。

在導航時，導向是以北方為基準，正向表示順時針，因此導向45°對應東北方。導向沒有負值，西北方對應的導向為315°。

其他量測角大小的方法

除了量測角本身的大小外．也有其他的方式，可以量測角的大小。

坡度等於一個角的正切值，常用百分比或千分比來表示。當一個角的坡度小於5%時，其坡度近似於角以弧度表示的數值。

在有理幾何學（英語：rational geometry）中，一個角的大小是以伸展度（spread）來表示，伸展度定義為角對應正弦的平方，而任一角正弦的平方和該角補角正弦的平方相等。因此任一角和其補角在有理幾何學中是等同的。

角的種類

個別的角

零角

角度等於0°，或弧度為0的角。

銳角

角度大於0°且小於90°，或弧度大於0且小於${\displaystyle {\frac {\pi }{2}}}$的角。

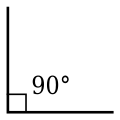
直角

角度等於90°，或弧度為${\displaystyle {\frac {\pi }{2}}}$的角。

鈍角

角度大於90°且小於180°，或弧度大於${\displaystyle {\frac {\pi }{2}}}$且小於${\displaystyle \pi }$的角。

平角

角度等於180°，或弧度為${\displaystyle \pi }$的角。

優角或反角

角度大於180°且小於360°，或弧度大於${\displaystyle \pi }$且小於${\displaystyle 2\pi }$的角。

周角

角度等於360°，或弧度為${\displaystyle 2\pi }$的角。

• 
  直角
• 
  優角（或作反角）
• 
  周角
• 
  銳角（a）、鈍角（b）和平角（c）

以下是各角度的名稱及不同單位下的數值：

名稱	零角	銳角	直角	鈍角	平角	優角	周角
單位	範圍
轉	${\displaystyle 0}$	${\displaystyle (0,{\tfrac {1}{4}})}$	${\displaystyle {\tfrac {1}{4}}}$	${\displaystyle ({\tfrac {1}{4}},{\tfrac {1}{2}})}$	${\displaystyle {\tfrac {1}{2}}}$	${\displaystyle ({\tfrac {1}{2}},1)}$	${\displaystyle 1}$
弧度	${\displaystyle 0\pi \,}$	${\displaystyle (0,{\tfrac {1}{2}}\pi )}$	${\displaystyle {\tfrac {1}{2}}\pi }$	${\displaystyle ({\tfrac {1}{2}}\pi ,\pi )}$	${\displaystyle \pi }$	${\displaystyle (\pi ,2\pi )}$	${\displaystyle 2\pi \,}$
度	${\displaystyle 0^{\circ }}$	${\displaystyle (0^{\circ },90^{\circ })}$	${\displaystyle 90^{\circ }}$	${\displaystyle (90^{\circ },180^{\circ })}$	${\displaystyle 180^{\circ }}$	${\displaystyle (180^{\circ },360^{\circ })}$	${\displaystyle 360^{\circ }}$

令x為該角度數。

角的組合

有三種特殊角的組合，其度數和均為特殊的值：

• 餘角：當兩個角的度數之和等於90°，即一個直角，這兩個角便是餘角。若兩個相鄰的角互為餘角，兩個非共用邊會形成直角。在歐幾里得幾何中，非直角的兩角即互為餘角。

若角A和B互為餘角，以下的數學式會成立：

${\displaystyle {\begin{aligned}\sin ^{2}A+\sin ^{2}B&=1\\\cos ^{2}A+\cos ^{2}B&=1\\\tan A&=\cot B\\\sec A&=\csc B\end{aligned}}.}$

（一角的正切等於其餘角的餘切，一角的正割等於其餘角的餘割）

三角函數中的餘函數，其前綴「co-」就是餘角的意思。

• 補角：當兩個角的度數之和等於180°，即一個平角，這兩個角便是互補角。若兩個相鄰的角互為餘角，兩個非共用邊會形成一直線。不過兩個不相鄰的角也可以是補角，例如平行四邊形中，任兩鄰角為互補角。圓內接四邊形的對角也是互補角。

若點P為圓O外的一點，而過點P作圓的切線，切點分別在點T和點Q，則∠TPQ和∠TOQ為互補角。

兩互補角的正弦相等，其餘弦及正切（若有定義義）大小相等，但符號異號。

在歐幾里得幾何中，三角形兩角的和為第三角的補角。

• explementary angles or conjugate angles. 當兩個角的度數之和等於360°

互為餘角的角a和角b

圖中的銳角和鈍角形成一組互補角

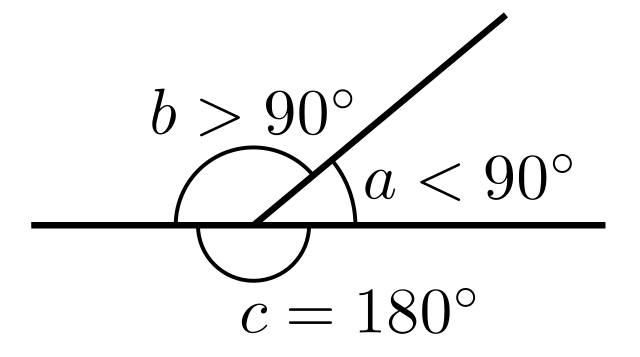
常用定理

同頂角

同頂角

${\displaystyle a+b+c=360^{\circ }}$

直線上的鄰角

直線上的鄰角

${\displaystyle a+b+c=180^{\circ }}$

與平行線有關的定理

與平行線有關的定理

當${\displaystyle AE}$平行於${\displaystyle BD}$,

• ${\displaystyle a=c}$（同位角，${\displaystyle AE//BD}$）
• ${\displaystyle b=d}$（內錯角，${\displaystyle AE//BD}$）
• ${\displaystyle b+c=180^{\circ }}$（同旁內角，${\displaystyle AE//BD}$）

由角度的關係也可以推得兩直線平行

• 當${\displaystyle a=c}$，${\displaystyle AE}$平行於${\displaystyle BD}$（同位角相等）
• 當${\displaystyle b=d}$，${\displaystyle AE}$平行於${\displaystyle BD}$（內錯角相等）
• 當${\displaystyle b+c=180^{\circ }}$，${\displaystyle AE}$平行於${\displaystyle BD}$（同旁內角互補）

二曲線的夾角

二曲線在P點的夾角定義為二曲線在P點切線A和B的夾角

曲線和直線的夾角或是二曲線間的夾角定義為二曲線在交點處切線的夾角。

點積及其拓展

在歐幾里得空間中，二個向量u及v的角和其點積及向量的長度有關：

${\displaystyle \mathbf {u} \cdot \mathbf {v} =\cos(\theta )\ \|\mathbf {u} \|\ \|\mathbf {v} \|.}$

依上式可以用二個平面（或曲面）的法向量，計算二者之間的夾角，也可以根據二歪斜線的向量計算其夾角。

內積

在一個抽象的實數內積空間中，在定義角時可以用內積 ${\displaystyle \langle \cdot ,\cdot \rangle }$取代歐幾里得空間的點積( · )：

${\displaystyle \langle \mathbf {u} ,\mathbf {v} \rangle =\cos(\theta )\ \|\mathbf {u} \|\ \|\mathbf {v} \|.}$

在複數的內積空間中，為了使餘弦的數值仍維持實數，因此需修改為

${\displaystyle \operatorname {Re} (\langle \mathbf {u} ,\mathbf {v} \rangle )=\cos(\theta )\ \|\mathbf {u} \|\ \|\mathbf {v} \|.}$

或者使用絕對值的標示：

${\displaystyle |\langle \mathbf {u} ,\mathbf {v} \rangle |=\cos(\theta )\ \|\mathbf {u} \|\ \|\mathbf {v} \|.}$

後者不考慮向量的方向，因此是描述由向量${\displaystyle \mathbf {u} }$及${\displaystyle \mathbf {v} }$所生成的二個一維子空間${\displaystyle \operatorname {span} (\mathbf {u} )}$及${\displaystyle \operatorname {span} (\mathbf {v} )}$之間的夾角。

黎曼幾何中的角

在黎曼幾何中，利用度量張量來定義二條切線之間的夾角，其中U及V是切線向量，g_ij 是度量張量G的分量。

${\displaystyle \cos \theta ={\frac {g_{ij}U^{i}V^{j}}{\sqrt {\left|g_{ij}U^{i}U^{j}\right|\left|g_{ij}V^{i}V^{j}\right|}}}.}$

地理學及天文學中的角

以地理的觀點，地球上任何一個位置都可以用地理座標系統來表示，此系統標示位置的經度及緯度，兩者都以此點連至地球球心連線的角度來表示，經度是以格林威治子午線為參考基準，而緯度是以赤道為參考基準。

在天文學中，天球的一點可以用任何一種天球坐標系統來表示，不過其基準則因坐標系統不同而不同。天文學量測二顆星星的角距離時，會假想分別有二顆星星分別和地球連成的直線，再量測這二條直線的夾角，即為角距離。

天文學家也會用角直徑量測一物體的表觀大小。例如滿月的角直徑約為0.5°。小角公式可以將上述的角測量轉換為距離和大小的比值。

相關條目

• 角平分線
• 輻角
• 圓心角
• 餘角
• 大圓距離
• 量角器
• 立體角
• 補角
• 無理角（英語：Irrational rotation）
• 角速度

參考資料

1. Heiberg, Johan Ludvig. Heath, T. L. , 編. Euclid. The thirteen books of Euclid's Elements 1. Cambridge University press. 1908: 177–178 [2012-08-24]. （原始內容存檔於2011-07-30）.
2. https://terms.naer.edu.tw/detail/b079b1a2250d7cff36338922ce22c5cd/
3. GB 3102.1-1993：空間和時間的量和單位（代替GB 3102.1-1986）．1993年12月27日公布，1994年7月1日實施．

外部連結

• 《中華人民共和國法定計量單位 （頁面存檔備份，存於網際網路檔案館）》