热门问题
时间线
聊天
视角
二分搜尋
有序列表的搜索算法,每次搜索过程将范围缩小一半 来自维基百科,自由的百科全书
Remove ads
二分查找(英語:binary search)[a]是用於查找有序數組中目標值位置的搜索算法。[11][2][12]二分查找比較目標值與數組中間元素的大小,如果兩者不相等,則會捨棄不可能包含目標值的那一半區間,然後在剩餘區間重複此過程:每次選取新的中間元素並與目標值比較,直至找到目標或區間為空。若區間為空,則說明目標值不存在。
二分查找在最壞情況下的時間複雜度為對數級別,即需做次比較,其中是數組元素的數量。[b][13]除規模較小的數組外,二分查找通常比線性搜索更快。二分查找的搜索效率可能不及哈希表等數據結構,但其還可用於查找最接近目標值的上界或下界,即使目標值不在數組中。
二分查找有許多其他形式。例如,分數級聯能加快在多個數組中查找同一數值的速度,還能高效地解決計算幾何等領域的搜索問題;指數搜索則將搜索範圍擴展至無界列表。二叉搜索樹和B樹等數據結構的實現也基於二分查找原理。
Remove ads
算法
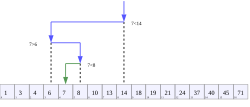
二分查找適用於有序數組。其首先比較數組中間的元素與目標值:如果目標值與該元素匹配,則返回其在數組中的位置;如果目標值小於該元素,則在數組較小的那一半中繼續查找;如果目標值大於該元素,則在數組較大的那一半中繼續查找。通過這種方法,每次迭代都能將搜索範圍縮小一半。[14]
給定包含個元素的數組,其中的值或記錄分別為,且滿足。假設目標值為。下面的子程序使用二分查找來尋找在數組中的索引。[14]
- 令為,為。
- 如果,則搜索失敗並終止。
- 令(中間元素的位置)為的向下取整值,即不大於的最大整數。
- 如果,則令為,回到步驟2。
- 如果,則令為,回到步驟2。
- 如果,則搜索完成,返回。
該過程使用兩個變量和來跟蹤搜索邊界。該過程可以用偽代碼表示如下,其中變量名和類型與上文相同,floor為下取整函數,unsuccessful表示搜索失敗時的特定返回值:[14]

function binary_search(A, n, T) is
L := 0
R := n − 1
while L ≤ R do
m := floor((L + R) / 2)
if A[m] < T then
L := m + 1
else if A[m] > T then
R := m − 1
else:
return m
return unsuccessful
也可令為的向上取整值。如此所做,若目標值在數組中出現多次,則結果可能會有所不同。
Remove ads
上述過程中,每次迭代都會檢查中間元素是否等於目標值。而在其他一些實現中,此檢查僅在最後剩餘一個元素(即)時執行,而每次迭代時不再執行比較。和前述過程相比,此方式平均多一輪迭代,但每輪迭代時少做一次比較。[15]
赫爾曼·博滕布魯赫於1962年首次發表了省略此檢查的實現。[15][16]
- 令為,為。
- 當時,
- 令(中間元素的位置)為的向上取整值,即不小於的最小整數。
- 如果,令為。
- 否則說明,令為。
- 現在,搜索完成。如果,返回。否則,搜索失敗並終止。
該版本的偽代碼如下,其中ceil是上取整函數:
function binary_search_alternative(A, n, T) is
L := 0
R := n − 1
while L != R do
m := ceil((L + R) / 2)
if A[m] > T then
R := m − 1
else:
L := m
if A[L] = T then
return L
return unsuccessful
Remove ads
若數組中有重複元素,算法會返回任一符合目標值的索引。例如,如果要搜索的數組為,且目標值為,那麼算法返回第4個至第7個元素(索引為3至6)都是正確的。然而,有時需要找到目標值在數組中重複出現的最左側或最右側的元素。在上述例子中,第4個元素是值為4的最左側元素,而第7個元素是值為4的最右側元素。若對應元素存在,上述的另一過程總是會返回最右側元素的索引。[16]
Remove ads
要查找最左邊的元素,可以使用以下過程:[17]
- 令為,為。
- 當時,
- 令(中間元素的位置)為的向下取整值,即不大於的最大整數。
- 如果,令為。
- 否則說明,令為。
- 返回。
如果且,那麼是等於的最左側元素。即使不在數組中,也是在數組中的排名,即數組中小於的元素數量。
該版本的偽代碼如下,其中floor是下取整函數:
function binary_search_leftmost(A, n, T) is
L := 0
R := n
while L < R do
m := floor((L + R) / 2)
if A[m] < T then
L := m + 1
else:
R := m
return L
Remove ads
要查找最右邊的元素,可以使用以下過程:[17]
- 令為,為。
- 當時,
- 令(中間元素的位置)為的向下取整值,即不大於的最大整數。
- 如果,令為。
- 否則說明,令為。
- 返回。
如果 且,那麼是等於的最右側元素。即使不在數組中,也是數組中大於的元素數量。
該版本的偽代碼如下,其中floor是下取整函數:
function binary_search_rightmost(A, n, T) is
L := 0
R := n
while L < R do
m := floor((L + R) / 2)
if A[m] > T then
R := m
else:
L := m + 1
return R - 1
Remove ads

二分查找不僅能精確定位目標值,也可方便地擴展到近似匹配,例如可以用來計算給定值的排名(即比它小的元素的數量)、前驅(前一個較小的元素)、後繼(下一個較大的元素)、最近鄰。而範圍查找(查找兩個值之間的元素數量)可利用查詢兩次排名得到。[18][19]
Remove ads
性能


二分查找的過程可以構建成一棵二叉樹,從而得到其比較次數並分析性能。樹的根節點是數組的中間元素,左半部分的中間元素是根節點的左子節點,右半部分的中間元素是根節點的右子節點,其餘部分以類似方式構建。搜索過程從根節點開始,根據目標值是小於還是大於當前節點的值來選擇遍歷左子樹還是右子樹。[13][23]
最壞情況下,二分查找需要比較次,此時搜索會達到樹的最深層。對於任何二分查找過程,樹的層數總為。若目標元素不在數組中,可能會發生最壞情況:若可以表示為2的某次冪減1,那麼查找過程總會遍歷到最深層,一定會發生最壞情況;否則,搜索過程可能會在倒數第二層中止,此時比較了次,比最壞情況少一次。[24]
平均情況下,當目標元素在數組中時,二分查找的比較次數是(假設每個元素被搜索的概率相等),近似於;若目標元素不在數組中,二分查找的比較次數平均為(假設範圍內及範圍外的元素被搜索的概率相等)。[23]
最好情況下,即目標值正好是數組的中間元素,二分查找在一次比較後就能返回其位置。[25]
從迭代次數的角度看,沒有任何一種僅通過比較元素大小進行搜索的算法,在平均情況和最壞情況下的性能優於二分查找。表示二分查找的比較樹除最底層外,每一層都是完全填滿的,因此層數最少。[c]如果不以此方式構造樹,搜索算法在每次迭代中只能排除較少的元素,從而增加平均情況及最壞情況下所需的迭代次數。其他基於元素比較的搜索算法便屬於這種情況:雖然它們查詢某些目標值時可能更快,但若綜合考慮所有元素,其平均性能均不及二分查找。二分查找每次將數組一分為二,保證兩個子數組的大小儘可能相近。[23]
Remove ads
二分查找需要使用三個指針(可能為數組索引,或指向內存地址的指針),與數組本身大小無關。因此,在word RAM計算模型中,二分查找的空間複雜度為。
二分查找的平均迭代次數取決於每個元素被搜索到的概率,而成功搜索與失敗搜索的平均情況不同。對於成功搜索,則需假設每個元素被搜索的概率相等;對於失敗搜索,則需假設數組元素之間及元素之外的每個區間被搜索的概率相等。成功搜索的平均情況是搜索數組中每個元素所需迭代次數之和除以元素數量,失敗搜索的平均情況則是搜索數組各區間所需迭代次數之和除以區間數量。[23]
在二叉樹的表示法中,一次成功搜索可以表示為從樹的根節點到目標節點的路徑,稱為「內部路徑」(internal path)。路徑長度等於路徑中經過的邊(節點之間的連接)數目。如果一條路徑長度為,則對應搜索所需的迭代次數為(包括初始迭代)。所有內部路徑長度之和稱作「內部路徑長度」(internal path length)。由於從根節點到任何特定節點僅存在一條路徑,因此每條內部路徑表示對特定元素的一次搜索。如果有個元素(為正整數),內部路徑長度記為,則成功搜索的平均迭代次數(其中表示初始迭代)。[23]
由於二分查找是基於元素比較的最優搜索算法,因此問題可簡化為求解含個節點的所有可能二叉樹中的最小內部路徑長度,表達式如下:[26]
例如,對於含7個元素的數組,根節點對應的搜索需1次迭代,下一層的兩個節點各需2次,再下一層的四個節點各需3次。因此,此時內部路徑長度為:[26]
根據成功搜索平均情況的公式,此時的平均迭代次數為。
上述內部路徑長度的求和公式可進一步化簡為:[23]
將此式代入成功搜索平均迭代次數的表達式中,得到:[23]
當為整數時,其與前述成功搜索的平均情況公式完全相同。
Remove ads
失敗搜索可在樹中增加額外節點以表示,這種結構稱為擴展二叉樹(extended binary tree)。當樹中已有節點(即內部節點)不足兩個子節點時,需為之添加額外的子節點(即外部節點),使每個內部節點都有兩個子節點。這樣一來,失敗搜索的過程便可表示為從根節點到外部節點的一條路徑,這個外部節點的父節點即為搜索結束時剩下的唯一元素。從根節點到外部節點的路徑稱為「外部路徑」(external path)。所有外部路徑的長度之和稱作「外部路徑長度」(external path length)。若元素個數為正整數,外部路徑長度為,則失敗搜索的平均迭代次數(其中表示初始迭代)。公式中除以而非的原因是,樹中有條外部路徑,它們分別表示數組元素之間以及數組邊界之外的各個區間。[23]
同樣地,這一問題可以簡化為確定含個節點的所有二叉樹中的最小外部路徑長度。對於任意二叉樹,外部路徑長度與內部路徑長度之間滿足。[26]將先前得到的表達式代入,則有:[23]
再將上式代入平均迭代次數的公式,便可求出失敗搜索的平均迭代次數:[23]
前文定義的二分查找過程,每次迭代需要做一次或兩次比較,其中每次迭代都會檢查中間元素是否與目標相等。假設每個元素被搜索到的概率均等,那麼平均每次迭代的比較次數為1.5次。還有一種實現方法是待搜索結束後,再檢查中間元素是否與目標值相等。平均而言,這種方法每次迭代可減少0.5次比較,略微降低了大部分計算機上每次迭代的運行時間。然而,這種方式一定會達到最多的迭代次數,搜索過程平均會額外增加一次迭代。因為即使在最壞情況下,二分查找的比較循環也只執行次,因此除非極大,否則每次迭代效率的微小提升不足以彌補額外增加的迭代次數。[d][27][28]
在分析二分查找的性能時,還需考慮比較兩個元素的所需的時間。整數和字符串的比較時間通常與其編碼長度(一般以位數表示)呈線性關係。假設逐位比較,與32位無符號整數相比,64位無符號整數的比較時間至多是前者最壞情況(即兩個整數相同)的兩倍。如果元素的編碼長度較大(例如大整數類型或長字符串),比較操作的開銷會顯著增加。此外,比較浮點數(實數在計算機中最常用的表示方式)通常也比整數和短字符串耗時更多。[29]
多數計算機架構中,CPU內部配有獨立於內存(RAM)的硬件緩存,容量極小但速度極快。因此,考慮到訪問局部性,多數CPU會存儲最近訪問的內存地址及其附近地址的數據。就數組而言,CPU訪問某個元素時,會同時緩存該元素以及在RAM中與之相鄰的元素,從而更快地順序訪問索引相近的數組元素。然而,二分查找每次跳躍到數組中點,內存跨度往往較大,不像線性搜索或哈希表的線性探測那樣具有良好局部性。因此查找較大數組時,實際耗時可能略高於理論預期。[29]
與其他方案的比較
在有序數組中,當插入和刪除操作與查找操作交替進行時,每次插入或刪除操作的時間複雜度為,效率低下。此外,有序數組的內存使用情況可能較為複雜,特別是在需要頻繁插入元素的情況下。[30]其他一些數據結構能更高效地支持插入與刪除操作。二分查找可以用於精確匹配和集合成員檢測(即判斷目標值是否存在於某個集合內)。雖然一些數據結構能夠更快地精確匹配與檢測集合成員,但二分查找還可用於高效地執行近似匹配,通常不論值的類型或結構如何,其近似匹配的性能都能達到。[31]此外,有序數組上還能高效完成一些操作,例如獲取最小值和最大值。[18][19]
線性搜索是簡單的搜索算法,其逐個檢查記錄,直到找到目標值為止。線性搜索可在鍊表上實現,其插入和刪除操作比數組更快。對於有序數組,除非數組很短,否則二分查找通常比線性搜索更快。不過二分查找需要提前對數組排序,[e][33]所有基於元素比較的排序算法(例如快速排序和歸併排序),最壞情況下都至少需要做次比較。[34]與線性搜索不同,二分查找還能高效地進行近似匹配。此外,在有序數組中,查找最大或最小元素等操作可以高效完成,而無序數組則無法做到。[35][36]

二叉搜索樹是基於二分查找原理構建的二叉樹數據結構。樹中元素按序排列,每個元素都可使用類似二分查找的方法執行搜索,其平均時間複雜度為對數級別。二叉搜索樹的插入和刪除操作平均也為對數時間,通常比有序數組插入和刪除的線性時間更快。同時,二叉樹也保留了有序數組的所有操作能力,包括範圍查詢和近似查詢。[31][37][38]
不過,二分查找在搜索操作上通常更高效,因為二叉搜索樹往往不是完美平衡的,性能會稍遜於二分查找。即使是平衡樹(能夠自我平衡的二叉搜索樹),也很少能達到理論上層數最少的狀態。非平衡二叉樹甚至可能嚴重失衡,內部節點(具有兩個子節點的節點)數量很少,此時的平均和最壞搜索性能可能接近次比較。[f]此外,二叉搜索樹占用的空間也比有序數組更大。[40][41]
二叉搜索樹在外部存儲設備(如硬盤)的搜索中具有優勢,因為可以在文件系統中有效組織。B樹推廣了這一樹結構的組織方式,常用於數據庫和文件系統等長期存儲系統。[42][43]
哈希表是將鍵映射到對應記錄的數據結構,一般使用哈希函數實現。對於關聯數組,哈希表通常比有序數組上的二分查找更快。[44]大部分哈希表的實現,其平均時間複雜度僅為平攤的常數時間。[g][46]但哈希表只在搜索失敗時告知目標不存在,而不能給出鄰近值的信息,因此不適合近似匹配,若執行查找下一個較小值、下一個較大值或者最近的鍵值等操作,效果不佳。[47]二分查找則非常適合近似匹配,且能在對數時間內完成。此外,諸如查找最大或最小元素等操作,在有序數組上可高效完成,而哈希表無法輕易做到。[31]
集合成員檢測是與搜索類似的問題,任何像二分查找這樣的搜索算法都可用於集合成員檢測。但也有一些專門用於集合成員檢測的算法。例如,當鍵值範圍有限時,位數組是最簡單的選擇。該結構緊湊地存儲一系列位,每位代表一個特定範圍內的鍵值。位數組的速度非常快,查詢僅需時間。[48]朱迪矩陣中的Judy1類型則能有效處理64位鍵值。[49]
對於近似結果,布隆過濾器是基於哈希函數的概率型數據結構,其使用位數組和多個哈希函數對鍵編碼,以存儲鍵集合。多數情況下,布隆過濾器比位數組的空間利用率更高,且速度也不會明顯變慢:若使用個哈希函數,成員查詢僅需時間。不過,布隆過濾器存在誤報問題。[h][i][51]
某些情況下,一些數據結構可能在搜索操作和其他適用於有序數組的操作上比二分查找更高效。對於搜索、近似匹配及有序數組上的一些操作,可以使用專門的數據結構,如van Emde Boas樹、融合樹、字典樹(trie)、位數組。這些數據結構通常只有在特定屬性的鍵值(如小整數鍵值)上更快,否則可能會導致時間或空間效率降低。[31]只要鍵值能被排序,這些操作在有序數組上仍能保持較高的效率。某些數據結構(如朱迪矩陣)結合了多種方法,不僅緩解了這些問題,還能保持較高效率,同時能夠近似匹配。[49]
其他形式

統一二分查找存儲的不是上下界,而是從當前中間元素到下一次迭代的中間元素間的索引差值,會將之事先存入查找表中。例如,要搜索的數組若為[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],當前的中間元素是6。此時,左側子數組[1, 2, 3, 4, 5]的中間元素是3,右側子數組[7, 8, 9, 10, 11]的中間元素是9。統一二分查找會存儲3這個差值(因為從6到左右兩個中間元素的索引距離都是3)。[52]為了縮小搜索空間,算法每次將這個差值與當前中間索引相加減。在某些不便於計算中點的系統(如十進制計算機)中,這種方法可能更快。[53]

指數搜索將二分查找擴展到無界列表。它先會查找首個索引為2的冪且元素大於目標值的位置,然後將該位置作為上界,再切換至二分查找。若目標值的位置為,則在開始二分查找之前,指數搜索最多需要進行次迭代,此後最多再進行次二分查找的迭代。指數搜索也適用於有界列表,但僅當目標值位於數組的開頭附近時,才比直接使用二分查找更高效。[54]

插值搜索不是每次計算中點,而是估算目標元素的位置。估算會考慮數組的最小值、最大值以及數組長度。其基本思路是:中點在很多情況下並非最理想的猜測位置。例如,如果目標值接近數組中的最大值,那麼目標值很可能靠近數組末尾。[55]
插值函數中最常見的是線性插值。設數組為,下界為,上界為,目標值為,則目標位置的估計值為。若使用線性插值,且數組元素分布均勻或接近均勻,則插值搜索的比較次數為。[55][56][57]
對於較小的數組,插值搜索由於有額外的計算開銷,其速度通常會比二分查找慢。儘管插值搜索的時間複雜度增長更慢,但只有在數組規模較大時,這種優勢才能抵消額外計算所需的開銷。[55]

分數級聯是用於在多個有序數組中快速搜索同一元素的技術。如果逐個搜索每個數組,時間複雜度為,其中為數組個數。分數級聯在每個數組中存儲關於元素在其他數組位置的信息,將時間複雜度降至。[58][59]
二分查找還被推廣到某些類型的圖結構,其中目標值存儲於圖的頂點中,而非數組元素內。二叉搜索樹即是這種推廣的特例。當在樹中查詢某個節點時,算法要麼確定這個節點就是目標,要麼知道目標元素所在的子樹位置。但推廣形式還可以更進一步:給定無向正權圖及目標頂點,每次查詢一個頂點時,算法要麼知道這個頂點就是目標,要麼獲得從該頂點到目標頂點的最短路徑上的某條邊信息。實際上,標準二分查找是圖為路徑時的特例,而二叉搜索樹則對應於當查詢的頂點不為目標時給出左或右子樹邊的情況。對於所有無向正權圖,均存在算法,最壞情況下也能通過次查詢,找到目標頂點。[60]

噪聲二分查找用於處理算法無法可靠地比較數組元素的情況,即比較每對元素大小時,都有一定概率出錯。噪聲二分查找可在給定的概率下確定目標元素正確的位置,這一概率控制着結果的可靠性。任何噪聲二分查找過程期望比較次數至少為,其中 為二元熵函數,表示最終輸出錯誤位置的概率。[61][62][63]噪聲二分查找問題也可視作Rényi-Ulam game的特例,[64]即基於20個問題的一種版本,其中回答可能會出錯。[65]
經典計算機執行二分查找時,在最壞情況下的迭代次數嚴格為。量子算法執行二分查找的查詢次數(對應經典算法的迭代次數)仍然與成正比,但常數因子小於1,因此在量子計算機上具有更低的時間複雜度。任何精確(即總能返回正確結果)的量子二分查找算法,最壞情況下至少需要次查詢(其中為自然對數)。[66]目前已經發現一種精確的量子二分查找算法,在最壞情況下的查詢次數為。[67]相比之下,格羅弗算法是用於搜索無序列表的最優量子算法,所需的查詢次數為。[68]
歷史
排序列表元素以提高查找效率,這一思想古已有之。目前已知最早的實例是約公元前200年巴比倫的「Inakibit-Anu」泥板,其包含約500個六十進制的數字及其倒數,數字按字典序排列,以便更快地找到特定的元素。此外,愛琴海諸島上也發現了一些按照姓名首字母排序的人名列表。1286年完成的拉丁語詞典《Catholicon》,首次給出了完整的字母排序規則,而不僅僅是依照單詞前幾個字母排序。[16]
1946年,約翰·莫奇利在摩爾學院講座(一門計算機科學領域的奠基性課程)中首次提及了二分查找。[16]1957年,威廉·韋斯利·彼得森發表了首個插值搜索算法。[16][69]早期的二分查找算法均只能用於長度為2的冪次減一的數組[j]。直至1960年,德里克·亨利·萊默提出適用於任意長度數組的二分查找算法。[71]1962年,赫爾曼·博滕布魯赫在ALGOL 60語言中實現了另一種二分查找版本,將判斷相等的比較操作放在末尾,雖使平均迭代次數增加了一次,但每次迭代所需的比較次數減少至一次。[15]統一二分查找則由斯坦福大學的A.K.錢德拉(A. K. Chandra)於1971年開發。[16]1986年,貝爾納·沙澤勒與利奧尼達斯·J·吉巴斯引入了「分數級聯」概念,用以解決計算幾何中的諸多查找問題。[58][72][73]
實現問題
总结
视角
儘管二分查找的基本思想相對簡單,但其細節卻出奇複雜。
喬恩·本特利在為職業程序員開設的一門課程中布置了二分查找的練習,發現90%的學生在數小時後仍未給出正確解答,主要問題是算法實現有誤而無法運行,或是在極少數邊緣案例下返回錯誤答案。[74]1988年發表的一項研究顯示,二十本教材中只有五本給出了準確的二分查找代碼。[75]此外,本特利自身在1986年出版的《編程珠璣》一書中給出的二分查找實現存在溢出錯誤,這個錯誤二十餘年未被發現。Java編程語言庫中的二分查找實現也存在相同的溢出問題,且該問題持續了九年多。[76]
在實際編程中,表示索引的變量通常是固定大小的整數。因此在處理非常大的數組時,可能會導致算術溢出。如果使用計算中點,即使和的值都在所用數據類型的表示範圍內,的值仍可能會超過範圍。如果和都是非負數,可以通過計算來避免這種情況。[77]
如果循環的退出條件定義不正確,可能會導致無限循環。當超過時,表示搜索失敗,必須返回失敗的信息。另外,循環應在找到目標元素時退出;若不這麼做,那麼在循環結束後,必須檢查是否成功找到目標元素。本特利發現,大多數在實現二分查找時出錯的程序員,都是退出條件出了錯。[15][78]
庫支持
許多編程語言的標準庫包含二分查找例程:
- C語言在其標準庫中提供了
bsearch()函數,通常使用二分查找實現,儘管官方標準中並未強制要求。[79] - C++的標準庫中提供了
binary_search()、lower_bound()、upper_bound()、equal_range()函數。[80] - D語言的標準庫Phobos在
std.range模塊中提供了SortedRange類型(由sort()和assumeSorted()函數返回),該類型包含contains()、equaleRange()、lowerBound()、trisect()方法,這些方法默認對提供隨機訪問的範圍使用二分查找技術。[81] - COBOL提供了
SEARCH ALL動詞,用於對COBOL有序表執行二分查找。[82] - Go的
sort標準庫包包含Search、SearchInts、SearchFloat64s、SearchStrings函數,分別實現了通用的二分查找,以及針對整數、浮點數、字符串切片的特定實現。[83] - Java在標準
java.util包的Arrays和Collections類中提供了一組重載的binarySearch()靜態方法,用於對Java數組和List(列表)執行二分查找。[84][85] - Microsoft的.NET Framework 2.0在其集合基類中提供了二分查找算法的靜態泛型版本,例如
System.Array的BinarySearch<T>(T[] array, T value)方法。[86] - 對於Objective-C,Cocoa框架在Mac OS X 10.6及以上版本中提供了
NSArray -indexOfObject:inSortedRange:options:usingComparator:方法;[87]蘋果的Core Foundation C框架也包含CFArrayBSearchValues()函數。[88] - Python提供了模塊
bisect,在插入元素後仍能保持列表的有序狀態,而無需每次插入元素後都對列表排序。[89] - Ruby的Array類包含帶有內置近似匹配的
bsearch方法。[90] - Rust的切片原始類型提供了
binary_search()、binary_search_by()、binary_search_by_key()、partition_point()方法。[91]
參見
- 乘性二分查找
注釋和參考文獻
- 任何僅通過元素比較進行搜索的算法,都可以用一棵二叉比較樹來表示。這棵樹中,從根節點出發,到達任意已存在節點的路徑稱為「內部路徑」(internal path)。定義為所有內部路徑的長度總和,即「內部路徑長度」(internal path length)。如果數組中的每個元素被搜索到的概率相等,那麼搜索算法的平均迭代次數為。換言之,該值即為樹中所有內部路徑長度的平均值再加上根節點處的第一次迭代。之所以如此,是因為內部路徑表示搜索算法在尋找目標元素時比較過的元素,而這些路徑長度則表示從根節點之後的迭代次數。因此,將這些路徑長度的平均值加上根節點處的一次迭代,即得到了平均情況的迭代次數。為讓平均比較次數最少,必須使內部路徑長度最小。事實上,二分查找構成的樹即滿足最小內部路徑長度的條件。Knuth(1998)證明,若樹中所有外部節點(即沒有子節點的節點)均位於連續的兩層內,則該樹的外部路徑長度(外部路徑即指所有從根節點到外部節點的路徑)最小。這一結論同樣適用於內部路徑,因為內部路徑長度與外部路徑長度存在線性關係(為樹的節點數)。當每個子樹的節點數量近似相同時(也就是每次迭代時都將數組大致分為兩半),樹中所有外部節點及其直接父節點都將位於連續兩層內。因此,二分查找對應的二叉比較樹具有最小的內部路徑長度,從而使得二分查找的平均比較次數達到最小。[23]
- Knuth(1998)使用其設計的MIX計算機模型發現,對於成功搜索而言,前述算法(即二分查找在每次迭代末尾檢查元素相等性)的平均運行時間為個單位,而標準二分查找的平均運行時間則為個單位。前者的時間複雜度增長稍慢,但初始複雜度更高。[27]
- Knuth(1998)對這兩種搜索算法的運行時間做了形式化分析。在Knuth設計的MIX計算機上,對於成功搜索,二分查找平均耗時為個單位;而在數組末尾加入哨兵節點的線性搜索平均耗時為個單位。線性搜索的計算量很少,故初始複雜度較低,但隨規模增長,其複雜度很快便會超過二分查找。在MIX計算機上,只有當時,二分查找的性能才會超過帶哨兵的線性搜索。[23][32]
外部連結
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
























![{\displaystyle [1,2,3,4,4,4,4,5,6,7]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4e1615253c99ebd1ef5b2997df4cf8ed852fa8ef)
















![{\displaystyle [20,30,40,50,80,90,100]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a2a762c441505aff6153082ad4c7863a26f52962)






















![{\displaystyle E(n)=I(n)+2n=\left[(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2\right]+2n=(n+1)(\lfloor \log _{2}(n)\rfloor +2)-2^{\lfloor \log _{2}(n)\rfloor +1}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/edbb46592a2cfed4a5d626d6080fd530bf7693b5)






































