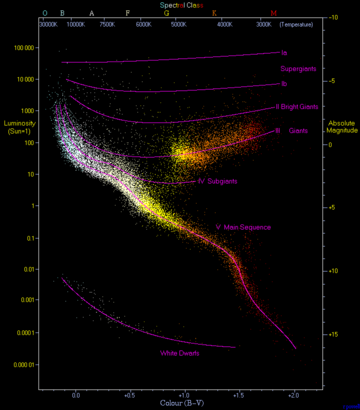
赫羅圖(英語:Hertzsprung–Russell diagram,簡寫為H–R diagram、HR diagram或HRD)是以恆星的絕對星等或光度相對於光譜類型或有效溫度繪製的散佈圖。更簡單的說,它將每顆恆星繪製在一張圖表上,可以測量它的溫度(顏色)和光度,而它與每顆恆星的位置無關。相關的顏色-星等圖(CMD,colour–magnitude diagram)繪製的是恆星的視星等和顏色,通常是針對恆星都在相同距離上的星團繪製。

這種圖表是埃納·赫茨普龍和亨利·諾利斯·羅素在1910年代創建的,是邁向了解恆星演化很重要的一步。
赫羅圖可顯示恆星的演化過程,大約90%的恆星位於赫羅圖左上角至右下角的帶狀上,這條線稱為主序帶。位於主序帶上的恆星稱為主序星。形成恆星的分子雲是位於圖中極右的區域,但隨著分子雲開始收縮,其溫度開始上升,會慢慢移向主序帶。恆星臨終時會離開主序帶,恆星會往右上方移動,這裏是紅巨星及紅超巨星的區域,都是表面溫度低而光度高的恆星。經過紅巨星但未發生超新星爆炸的恆星會越過主序帶移向左下方,這裏是表面溫度高而光度低的區域,是白矮星的所在區域,接著會因為能量的損失,漸漸變暗成為黑矮星。
歷史的背景
在19世紀,哈佛大學天文台對恆星進行了大規模的攝影光譜調查,獲得數十萬顆恆星的光譜,並加以分類,最終完成了亨利·德雷伯目錄。安東妮亞·莫里參與了這項工作的一個部分,她依據譜線的寬度來分類恆星[1]。赫茨普龍指出,以窄譜線描述的恆星自行比同一光譜類型的其它恆星小。他認為這是窄譜線的恆星有更大光度的指示,並計算了一些群組的長期視差,讓他可以估計其絕對星等[2]。
在1910年,漢斯·羅森伯格發表了一張圖表,以鈣線相對於氫的兩條巴耳末線的強度繪製昴宿星團中恆星的視星等[3]。這些譜線作為恆星溫度的代理,是光譜分類的早期形式。在同一個星團中,恆星的視星等等同於它們的絕對星等,所以這張早期的圖實際上就是一個與溫度有關的光度圖。今天,依然使用相同類型的圖來顯示星團中的恆星,而無須知道它們的距離和亮度[4]。赫茨普龍也已經在使用這種類型的圖表,但直到1911年他才首次在他的出版品中顯示出來。這也是使用星團中有著相同距離恆星簇視星等圖的型式[5]。
羅素早期(1913年)版本的圖包括由安東妮亞·莫里分類,經赫茨普龍確認的巨星,以及當時已經測量出視差的近距離恆星,和畢宿星團(附近的疏散星團)以及一些移動星群中的恆星;這些都可以測量距離,從而獲得這些恆星的絕對星等[6].
圖的形式
赫羅圖有好幾種型式,但在命名上都沒有很好的定義。所有的型式都有共同的常規佈局:亮度較大的恆星分布在圖的頂端,表面溫度高的恆星分布在圖的左側。
原始的圖在水平軸上顯示恆星的光譜類型,在垂直的軸上顯示絕對視星等。光譜類型不是數值的量,但其序列反映出恆星表面溫度的單調序列。現代觀測版本的圖表將光譜類型替換成色指數(在20世紀的圖表中,最常見的是恆星的B-V色指數)。這種類型的圖表通常稱為觀測赫羅圖,或特殊的色光圖(CMD,color–magnitude diagram),並且通常是觀測者在使用[7]。在已知恆星處於相同距離(如恆星簇內)的情況下,CMD通常用於描述星團中的恆星,其垂直軸視恆星的視星等。對於群聚的成員,假設所有恆星簇的視星等和絕對星等(稱為距離模數)之間存在著單一的加法常數差。早期對附近疏散星團(像是畢宿星團和昴宿星團)的研究,赫茨普龍和羅森伯格得到了第一張的CMD圖,受到早些年羅素蒐集所有恆星圖的影響,綜合的資料可以確定恆星的絕對星等[3][5]。
圖的另一種形式是在一個軸上繪製恆星的有效表面溫度,另一個軸是恆星的光度,並且幾乎都是用雙對數坐標系。恆星結構和恆星演化的理論計算產生的圖和觀測結果相符。這種圖稱為「溫度光度圖」,但是這個名稱幾乎沒有使用過;當在區分時,這種形式被「理論赫羅圖」的名稱取而代之。這種形式赫羅圖的特點是,溫度的繪製是從高溫到低溫,這有助於和觀測型式的圖做比較。
雖然這兩種圖是相似的,但天文學家在兩者之間做了明顯的區分。這樣區分的原因是,從一個圖精確地轉換到另一個圖並不是簡單的事。在有效溫度和顏色之間的轉換,需要色溫關係,而建構這種關係是很困難的;眾所周知,這是恆星組成的函數,並且會受到其它因素(例如恆星自轉)的影響。當將光度或絕對全波段星等(熱星等)轉換為視星等或絕對目視星等時,需要全波段校正,這可能是也可能不是與色溫圖有相同的關聯性。此外還需要知道與觀測到的物體(即距離模數)和星際遮蔽的效應,這在顏色(紅化)和視星等(其效果稱為消光)兩者上都有影響。顏色的失真(包括紅化)和消光(遮蔽)在有顯著星周塵的恆星上也很明顯。對恆星演化的理論直接和觀測比較是較理想的做法,因為在理論和觀測之間的轉換會產生額外的不確定性。
解釋
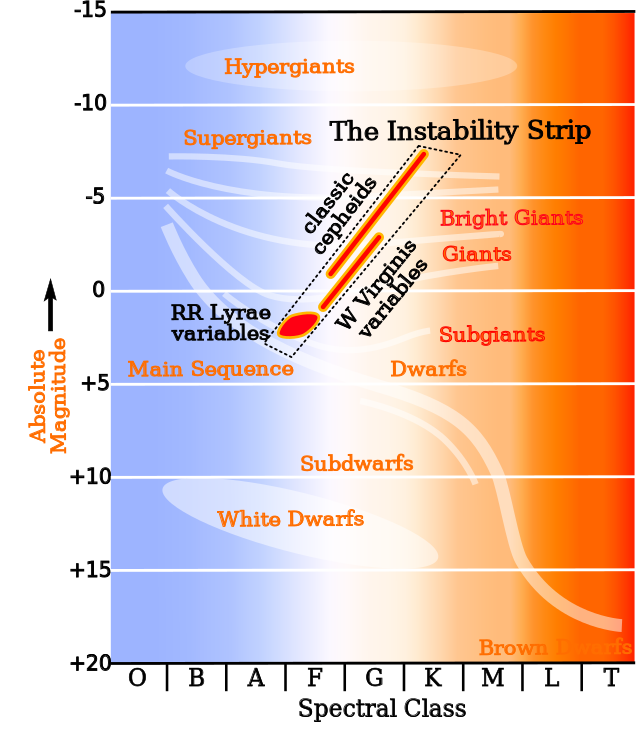
大多數恆星分布在圖中被稱為主序帶的對角線區域上。這些恆星在主序帶上的生命階段,它們在核心的核融合反應是氫融合。在下一個階段濃縮的恆星是在水平分支(在核心是氦融合,氫融合在圍繞在核心附近的殼層中進行)。另一個突出的特徵是位於光譜類型A5和G0之間,絕對星等+1和-3之間區域內的赫氏空隙(也就是在主序帶上方與水平分支的巨星之間)。在空隙的左邊被稱為不穩定帶的區間可以發現天琴座RR型變星的恆星。造父變星也落在不穩定帶上光度較高的區間上。
天文學家可以利用赫羅圖大致測量出星團或星系距離地球有多遠。這可以通過將星團中恆星的視星等與已知距離(或模型恆星)的絕對星等進行比較來實現。然後將觀察的整組在垂直方向移動,直到兩者的主序帶重疊。為了匹配兩個群組而橋接的星等差異稱為距離模數,也就是直接測量出的距離(忽略消光的因素)。這種技術稱為主序列擬合,是光譜視差的一種。不僅主序列中的轉折點可以使用,紅巨星分支的尖端也可以使用[8][9]。
歐空局的蓋亞任務在圖中顯示了一些未知或懷疑存在的特徵。 它在M矮星的主序帶中發現了一個間隙,這可以透過從部分對流核心到完全對流核心的轉變來解釋[10][11]。 對於白矮星,該圖顯示了幾個特徵。 此圖中出現了兩個主要的濃度,遵循白矮星的冷卻順序,這可以透過白矮星的大氣成分來解釋,特別是白矮星的氫與氦為主的大氣[12]。 第三種濃度可以用白矮星內部的核心結晶來解釋。 這會釋放能量並延遲白矮星的冷卻[13][14]。
圖在恆星物理學發展中的作用

對這張圖的思考使天文學家推測,它可能會證明恆星演化,主要的說法是從紅巨星墜落到矮星,然後在它的一生中沿著主序列向下移動。因此,恆星被認為是通過克爾文-赫爾姆或茲機制將重力能轉化為輻射來輻射能量。這種機制導致太陽的年齡只有數千萬年,在太陽系的年齡問題上,天文學家與生物學家和地質學家之間發生了衝突,而他們有證據表命地球比這古老得多。這場衝突到1930年代,當核融合被確定為恆星的能量來源時,才獲得解決。
在羅素於英國皇家天文學會於1912年的會議上介紹了該圖之後,亞瑟·愛丁頓受到啟發,將其作為發展恆星物理學思想的基礎。在1926年,他在《恆星的內部結構》一書中解釋了恆星如何融入圖的物理學[15]。這篇論文預期了後期發現的核融合,並正確的提出恆星的動力來源是氫融合成氦,釋放出巨大的能量。這是一個卓越的洞燭先機的躍遷,因為那時還未解決恆星的能量來源,尚未證明存在熱核能量,甚至尚未發現恆星主要是氫(參見金屬量)。愛丁頓設法避開了這個問題,集中注意在恆星內部能量的熱力學[16]。愛丁頓預測,矮星在一生的大部分時間裡,在主序帶上基本保持著靜態的位置。在20世紀的30年代和40年代,隨著對氫融合的理解,出現了證據支持紅巨星演化的論述,隨後又推測白矮星是爆炸和崩潰殘骸的案例。超新星核合成這個術語是弗雷德·霍伊爾在1954年提出的[17]。純數學的量子力學和經典力學模型的恆星過程,使赫羅圖被註解與已知的常規路徑稱為恆星序列-隨著更多罕見、異常例子的增加,才有更多恆星的分析和數學模型被考慮。
赫羅圖與星球體積的大小關係
物理學家在研究熱輻射光譜的時候,發現了在一個單位面積上,亮度與溫度之間的關係。溫度越高亮度越亮。因此,一旦我們能夠決定一個星球的絕對星等和光譜類型,我們就能估計它的體積大小。
單位時間內,在單位面積中所釋放出來的熱輻射能量與溫度四次方成正比。
- (σ為史蒂芬·波茲曼常數)
光度為單位時間內熱輻射所發出來的能量,所以將上式乘上星球總面積,假設星球為球形:
所以在赫羅圖上,我們也可以把相同表面積的星球,出現的位置用連線標示出來。我們可以看到,在圖的右上方,低溫且高光度,所以是體積很大的星球。越往左下方高溫且低光度,所以體積越來越小。
赫羅圖上恆星質量大小
在觀察恆星時由雙星系統,經由研究這兩個星星之間引力所造成的軌道運動可以決定這兩個星星的質量。在主序列帶上的恆星,是按照質量大小排列的。在左上方,高溫高亮度的是質量比較大的恆星,而在右下方低溫低亮度的則是小質量的恆星。
星團赫羅圖
由於一個星團中的恆星距離基本一致(或者一個遙遠星系中的星團距離基本一致),因此可以用視星等取代絕對星等作為縱軸繪製星團中成員恆星的赫羅圖或者遙遠星系中成員恆星的赫羅圖。星團赫羅圖與標準赫羅圖的比較,可以幫助估計星團的實際距離。
相關條目
參考資料
外部連結
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.