杠杆

此条目介绍的是物理学中的杠杆原理。关于化学领域的同名概念，请见“杠杆原理 (化学)”。

在力学里，典型的杠杆是置放连结在一个支撑点上的硬棒，这硬棒可以绕著支撑点旋转。当杠杆静力平衡时，其施力乘以施力臂等于抗力乘以抗力臂，可以透过改变施力臂或抗力臂长度，使输入力放大或缩小，有著相当实用的功能，古希腊人将杠杆归类为简单机械。^[1]

杠杆
遵守杠杆原理，置放在杠杆上的两个重物呈静力平衡状态。
分类	简单机械

历史

1824年，在伦敦发行的《机械杂志》内的一副刻画。阿基米德说：“给我一个支点，我就可以撬起整个地球。”

早在旧石器时代晚期，古人就知道使用杠杆的原理来制作投枪器。 ^[2] 考古学者认为，在古埃及4500多年前的金字塔时期，工人使用杠杆来移动、抬举重量超过100英吨的方尖碑。^[3] 中国战国时期，墨子在所著作的《墨子》一书中，提到应用杠杆的概念。^{[注 1][4][5]}

大约在西元前330年，亚里斯多德在著作《机械问题》（《Mechanical Problems》）里，对于杠杆有详细的论述，并且基本而言使用虚功的现代概念推导出杠杆原理。^[6]西元前3世纪，古希腊科学家阿基米德在著作《论平面图形的平衡》里用几何方法推导出杠杆原理，^[7]并且宣称：“给我一个支点，我就可以撬动整个地球。”^{[注 2][8]}

概述

静力平衡的杠杆。

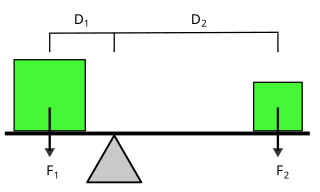
由于杠杆内部有一点为固定点，杠杆只能绕著这固定点做旋转运动。相对于这一点，杠杆不能做平移运动。

• 杠杆内部的固定点称为“支点”。
• 使杠杆旋转的力 ${\displaystyle F_{1}}$ 叫做“施力”，是输入力。
• 施力作用于杠杆的位置叫做“施力点”。
• 阻碍杠杆旋转的力 ${\displaystyle F_{2}}$ 叫做“抗力”，是输出力。
• 抗力作用于杠杆的位置叫做“抗力点”。
• 从支点到施力作用线的垂直距离 ${\displaystyle D_{1}}$ 叫做“施力臂”。
• 从支点到抗力作用线的垂直距离 ${\displaystyle D_{2}}$ 叫做“抗力臂”。

理想杠杆不会耗散或储存能量，也就是说，支点与硬棒之间不会出现任何摩擦损耗，硬棒是一种刚体，不会被弯曲，发生形变。注意到硬棒不一定是直棒。弯曲的硬棒形成的杠杆称为“曲杠杆”。对于理想杠杆案例，输入杠杆的功率等于杠杆输出的功率。输出力与输入力之间的比率，等于这两个作用力分别与支点之间垂直距离的反比率，称这相等式为“杠杆原理”，以方程式表达：

${\displaystyle F_{2}:F_{1}=D_{1}:D_{2}}$ ，

或者，

${\displaystyle F_{1}D_{1}=F_{2}D_{2}}$ 。

定义力矩 ${\displaystyle M}$ 为

${\displaystyle M\ {\stackrel {def}{=}}\ FD}$ ；

其中，${\displaystyle F}$ 是作用力，${\displaystyle D}$ 是作用力与支点之间的垂直距离。

则输入力矩等于输出力矩：

${\displaystyle M_{1}=M_{2}}$ 。

杠杆原理表明，当静力平衡时，施力乘以施力臂等于抗力乘以抗力臂：

${\displaystyle F_{1}D_{1}=F_{2}D_{2}}$ 。

杠杆的分类

靠著比较施力臂、抗力臂的长度，可以将杠杆分为三类：

• 施力臂长于抗力臂的杠杆是“省力杠杆”，这可以省力。开瓶器、撬棍等均为省力杠杆。
• 抗力臂长于施力臂的是“费力杠杆”，这可以省时。大部分剪刀、镊子、筷子、钓鱼竿、火钳、笔等均为费力杠杆。
• 施力臂和抗力臂长度相等的杠杆是“等臂杠杆”，跷跷板、天秤等均为等臂杠杆。

另外一种分类法式依照施力点、抗力点、支点在杠杆的相对位置来分类。^[9]

第一类杠杆

第一类杠杆的施力点、抗力点分别在支点的两边。例如，铁撬、跷跷板、天平、尖嘴钳。

第二类杠杆

第二类杠杆的施力点、支点分别在抗力点的两边。例如，独轮车、胡桃钳、开瓶器。这是一种省力杠杆，可以施加较小的力量来移动较重的物体，但是施力的位移较长.

第三类杠杆

第三类杠杆的抗力点、支点分别在施力点的两边。例如，镊子、钉书机、扫把。这是一种费力杠杆，可以节省施力的位移。

杠杆原理

杠杆是可以绕著支点旋转的硬棒。当外力作用于杠杆内部任意位置时，杠杆的响应是其操作机制；假若外力的作用点是支点，则杠杆不会出现任何响应。

假设杠杆不会耗散或储存能量，则杠杆的输入功率必等于输出功率。当杠杆绕著支点呈匀角速度旋转运动时，离支点越远，则移动速度越快，离支点越近，则移动速度越慢，由于功率等于作用力乘以速度，离支点越远，则作用力越小，离支点越近，则作用力越大。

静力平衡的杠杆。

机械利益是抗力与施力之间的比率，或输出力与输入力之间的比率。假设施力臂 ${\displaystyle D_{1}}$ 、抗力臂 ${\displaystyle D_{2}}$ 分别为施力点、抗力点与支点之间的距离，施力 ${\displaystyle F_{1}}$ 、抗力 ${\displaystyle F_{2}}$ 分别作用于施力点、抗力点。则机械利益 ${\displaystyle MA}$ 为

${\displaystyle MA={\frac {F_{2}}{F_{1}}}={\frac {D_{1}}{D_{2}}}}$ 。

通常在学习杠杆的初级理论时，会聚焦于输入力和输出力由于虚位移而做的虚功。虚位移可以定义为物体的移动速度乘以虚时间。这样定义导致计算的物理量是功率，而不是功。这种方法有一个实在优点：在研究机械工程学或机构学时，功率是主要计算的物理量。使用这种方法来对杠杆做静力分析，就如同对于车子的传动系统，或机械手臂做静力分析，它们的机械利益的计算方式完全一样。

复式杠杆

指甲剪是一种常用的复式杠杆。

复式杠杆是一组耦合在一起的杠杆，前一个杠杆的抗力会紧接地成为后一个杠杆的施力。几乎所有的磅秤都会应用到某种复式杠杆机制。其它常见例子包括指甲剪、钢琴键盘。1743年，英国伯明罕发明家约翰·外艾特（英语：John Wyatt）在设计计重秤时，贡献出复式杠杆的点子。他设计的计重秤一共使用了四个杠杆来传输负载。^[10]

参阅

• 连杆组
• 机构学
• 单摆

注释

1. 负：衡木加重焉而不挠，极胜重也。右校交绳，无加焉而挠，极不胜重也。衡加重于其一旁必捶，权重相若也。相衡则本短标长，两加焉重相若，则标必下，标得权也。
   挈：有力也，引无力也。不正所挈之止于施也，绳制挈之也，若以锥刺之。挈，长重者下，短轻者上，上者愈得，下下者愈亡。绳直权重相若，则正矣。收，上者愈丧，下者愈得，上者权中尽，则遂。

   ——《墨子·经说下》第二六、二七条

2. 假设在与地心引力相同的均匀重力场做这表演，在一端为与地球质量相同的圆球，离支点距离1m，在另一端为70kg质量的实验者，则实验者与支点的距离为8.5×10²²m。这距离大约是仙女座星系与地球之间距离的3.6倍。

参考文献

1. Moon, Francis; Moon, F. C., The machines of Leonardo da Vinci and Franz Reuleaux:kinematics of machines from the Renaissance to the 20th century illustrated, annotated, Springer: pp. 28, 2007, ISBN 9781402055980 引文格式1维护：冗余文本 (link)
2. Humphrey, John. Ancient technology illustrated. Greenwood Publishing Group. 2006: 17-18. ISBN 9780313327636.
3. Budge, E.A. Wallis. Cleopatra's Needles and Other Egyptian Obelisks. Kessinger Publishing. 2003: pp. 28. ISBN 9780766135246. 引文格式1维护：冗余文本 (link)
4. 吴毓江，墨子校注，北京：中华书局，1993年，第533页
5. 墨子. 《經說下》. 中国哲学书电子化计划. （原始内容存档于2021-03-07）.
6. Cotterell, Brian; Kamminga, John, Mechanics of pre-industrial technology: an introduction to the mechanics of ancient and traditional material culture illustrated, reprint, Cambridge University Press: pp. 75–76, 1992, ISBN 9780521428712 引文格式1维护：冗余文本 (link)
7. Usher, Abbott. A history of mechanical inventions revised, illustrated. Courier Dover Publications. 1988: pp. 94. ISBN 9780486255934. 引文格式1维护：冗余文本 (link)
8. Mackay, Alan Lindsay. Archimedes ca 287–212 BC. A Dictionary of scientific quotations. London: Taylor and Francis. 1991: pp. 11. ISBN 9780750301060. 引文格式1维护：冗余文本 (link)
9. Davidovits, Paul, Physics in Biology and Medicine, Third edition, Academic Press: pp. 10, 2008, ISBN 978-0-12-369411-9 引文格式1维护：冗余文本 (link)
10. Ceccarelli, Marco. Distinguished Figures in Mechanism and Machine Science: Their Contributions and Legacies. Dordrecht: Springer. 2007: 16 [2010-01-17]. ISBN 1402063652. Then in 1743 John Wyatt (1700–1766) introduced the idea of the compound lever, in which two or more levers work together to further reduce effort.

外部链接

• 中国古代机械工程网页：杠杆 （页面存档备份，存于互联网档案馆）。