双新月双丸塔

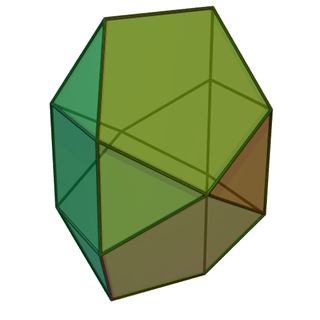
双新月双罩帐（Bilunabirotunda）是约翰逊多面体的其中一个，索引为J₉₁。它无法由柏拉图立体（正多面体）和阿基米得立体（半正多面体）经过切割、增补而得来，是詹森多面体中的基本立体之一。詹森多面体是凸多面体，面皆由正多边形组成但不属于均匀多面体，共有92种。这些立体最早在1966年由诺曼·詹森（英语：Norman Johnson (mathematician)）（Norman Johnson）命名并给予描述^[1]。

双新月双罩帐

类别	詹森多面体 J90 - J91 - J92
识别
名称	双新月双罩帐
参考索引	J91
鲍尔斯缩写 （verse-and-dimensions的wikia：Bowers acronym）	bilbiro
性质
面	14
边	26
顶点	14
欧拉特征数	F=14, E=26, V=14 （χ=2）
组成与布局
面的种类	2×4个正三角形 2个正方形 4个五边形
顶点图	4个(3.52) 8个(3.4.3.5) 2个(3.5.3.5)
对称性
对称群	D2h群
特性
凸
图像
（对偶多面体） （展开图）
查 论 编

性质

双新月双罩帐共由14个面、26条边和14个顶点组成^[2][3][4]。在其14个面中，有8个正三角形、2个正方形和4个五边形^[2]。在其14个顶点中，有2个顶点是2个三角形和2个五边形的公共顶点^[4]，并且这些面在构成顶角的多面角时，以三角形、五边形、三角形和五边形的顺序排列，在顶点图中可以用(3.5.3.5)来表示^[4]，或者简写为[(3,5)²]^[5]；还有8个顶点是2个三角形、1个正方形和1个五边形的公共顶点^[4]，并且这些面在构成顶角的多面角时，以三角形、正方形、三角形和五边形的顺序排列，在顶点图中可以用(3.4.3.5)^[4]或[3,4,3,5]^[5]来表示；剩下的4个顶点是1个三角形和2个五边形的公共顶点，在顶点图中可以用(3.5²)^[4]或[3,5²]^[5]来表示。

双新月双罩帐是诺曼·詹森（英语：Norman Johnson (mathematician)）列表末尾的特殊詹森多面体之一，它无法由柏拉图立体（正多面体）和阿基米得立体（半正多面体）经过切割、增补而得来，然而，它与截半二十面体有关：其名称中的“罩帐”部分是指围绕一个顶点的两个五边形和两个三角形的配置，它实际上是正五角罩帐（J₆）表面的一部分，正五角罩帐也可以视为截半二十面体的一半。诺曼·詹森将其名称中的“新月”部分定义为位于罩帐部分两侧的三角形-正方形-三角形带。在正五角罩帐表面的部份有两个这样的部分和两个这样的“新月”部分，因此称双新月双罩帐。^[3]

二面角

双新月双罩帐有五种二面角，分别为两种三角形与正方形的二面角，以及两种三角形与五边形的二面角以及一种五边形和五边形的二面角。^[5]

其中，两种三角形与正方形的二面角分为在“新月”部分上的，以及“新月”与“罩帐”交错部分的。^[5]

其中，“新月”部分上的三角形与正方形的二面角角度约为159.09度：^[5]

${\displaystyle \arccos \left(-{\frac {1+{\sqrt {5}}}{\sqrt {12}}}\right)\approx 2.7767288\approx 159.094843^{\circ }}$

而“新月”与“罩帐”交错部分的三角形与正方形的二面角角度约为110.9度：^[5]

${\displaystyle \arccos \left(-{\sqrt {\frac {3-{\sqrt {5}}}{6}}}\right)\approx 1.935660\approx 110.905157^{\circ }}$

两种三角形与五边形的二面角分为在“罩帐”部分上的，以及“新月”与“罩帐”交错部分的。^[5]

其中，“罩帐”部分上的三角形与五边形的二面角角度约为142.62度：^[5]

${\displaystyle \arccos \left(-{\sqrt {\frac {5+2{\sqrt {5}}}{15}}}\right)\approx 2.48923451\approx 142.622632^{\circ }}$

而“新月”与“罩帐”交错部分的三角形与五边形的二面角角度约为100.81度：^[5]

${\displaystyle \arccos \left(-{\sqrt {\frac {5-2{\sqrt {5}}}{15}}}\right)\approx 1.75950686\approx 100.812317^{\circ }}$

而五边形和五边形的二面角为5的平方根倒数的反馀弦值，角度约为63.43度：^[5]

${\displaystyle \arccos \left({\frac {1}{\sqrt {5}}}\right)\approx 1.1071487\approx 63.434949^{\circ }}$

顶点座标

几何中心位于原点且边长为单位长的双新月双罩帐顶点座标为：^[6]

${\displaystyle \left(0,0,\pm {\frac {\varphi }{2}}\right)}$

${\displaystyle \left(\pm {\frac {\varphi +1}{2}},\pm {\frac {1}{2}},0\right)}$

${\displaystyle \left(\pm {\frac {1}{2}},\pm {\frac {\varphi }{2}},\pm {\frac {1}{2}}\right)}$

其中，${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}$为黄金比例。

相关多面体

6个双新月双罩帐可以围绕一个立方体形成一个五角十二面体群对称的结构。邦妮·麦迪逊·斯图尔特（英语：Bonnie Stewart）将这种6个双新月双罩帐的模型标示为6J₉₁(P₄).^[7]

该结构与正十二面体结合可以完成空间填充，也就是结合了双新月双罩帐、立方体和正十二面体的空间填充。^[8]

空间填充

6个双新月双罩帐可以围绕一个立方体

双新月双罩帐、立方体和正十二面体之空间填充的动画 12个双新月双罩帐围绕一个正十二面体

双新月双罩帐可以在五边形面上叠上锥体构成侧锥双新月双罩帐，然而若要确保所有面皆为正多边形时，其会变为共面的多面体，因此只能算做拟詹森多面体。特别地，侧锥双新月双罩帐和异侧邻二侧锥双新月双罩帐因所有顶点都严格位于顶角上，因此属于78个条件边正多边形凸多面体之一^[9]。

侧锥数量	0	1	2			3	4
图像	双新月双罩帐	侧锥双新月双罩帐	对二侧锥双新月双罩帐	邻二侧锥双新月双罩帐	异侧邻二侧锥双新月双罩帐	三侧锥双新月双罩帐	四侧锥双新月双罩帐

参见

• 约翰逊多面体
• 多面体

参考文献

1. Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics（英语：Canadian Journal of Mathematics）, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8
2. David I. McCooey. Johnson Solids: Bilunabirotunda. [2022-09-07]. （原始内容存档于2022-09-09）.
3. The Bilunabirotunda. qfbox.info. [2022-09-09]. （原始内容存档于2022-09-09）.
4. Bilunabirotunda. polyhedra.tessera.li. [2022-09-09]. （原始内容存档于2022-09-09）.
5. Richard Klitzing. bilunabirotunda, bilbiro. bendwavy.org. [2022-09-09]. （原始内容存档于2022-11-14）.
6. David I. McCooey. Data of Bilunabirotunda. [2022-09-07]. （原始内容存档于2022-09-09）.
7. B. M. Stewart. Adventures Among the Toroids: A Study of Quasi-Convex, Aplanar, Tunneled Orientable Polyhedra of Positive Genus Having Regular Faces With Disjoint Interiors. 1980. ISBN 978-0686119364. (page 127, 2nd ed.) polyhedron 6J₉₁(P₄).
8. Miracle Spacefilling (Dodecahedron&Cube&Johnson solid No.91). woodenpolyhedra.web.fc2.com. [2022-09-09]. （原始内容存档于2022-09-09）.
9. Robert R Tupelo-Schneck. Convex regular-faced polyhedra with conditional edges. [2023-02-01]. （原始内容存档于2021-08-18）.

外部链接

• 埃里克·韦斯坦因. Johnson Solid. MathWorld.
  • 埃里克·韦斯坦因. Bilunabirotunda. MathWorld.