结构化程式理论也称为伯姆-贾可皮尼理论或Böhm-Jacopini理论[1][2]，是一项程式语言研究的结果，说明只要一种程式语言可以依三个方式组合其子程式及调整控制流程，每个可计算函数都可以用此种程式语言来表示。三个调整控制流程的方式为
- 执行一个子程式，然后执行下一个（顺序）
- 依照布尔变数的结果，决定执行二段子程式中的一段（选择）
- 重复执行某子程式，直到特定布尔变数为真为止（循环）
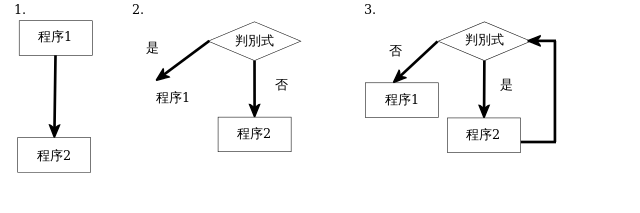
符合上述条件的结构图需要额外的位元变数（在原始证明中放在额外的整数变数中），以纪录原来程式执行到的位置，此种建构法是以伯姆的程式语言P′′为基础。
起源及变体
一般认为[3]:381此理论最早是在1966年科拉多·伯姆及朱塞佩·贾可皮尼（Giuseppe Jacopini）的论文中提出[4]。大卫·哈雷尔在1980年曾提到这篇论文广受认可，[3]:381尤其在结构化程式理论的支持者中。哈雷尔也提到“由于其论文比较技术的风格，因此较常被引用，较少人真正详读过内容。”[3]:381，在看了1980年以前的大量论文后，哈雷尔认为结构化程式理论被错误诠释为一个结果较简单的大众定理（folk theorem），而此结果可以追溯到冯·诺依曼及斯蒂芬·科尔·克莱尼现代计算理论的论文[3]:383。
哈雷尔也提到较通用的“结构化程式理论”名称是在1970年代初由哈伦·米尔斯提出[3]:381。
此版本的定理将原来定理中的程式控制流程改为一个while回圈，模拟在原来非结构化的程式中，程式计数器走过所有可能标记（流程图方块）的情形。哈雷尔将此版大众定理的源头追溯到两篇论文，一篇是1946年描述冯·诺伊曼结构，用单一while回圈说明程式计数器的运作原理，哈雷尔也注意到大众定理中用到的单一回圈基本上可以提供冯·诺伊曼式电脑执行流程的操作语义。[3]:383。另一篇更早期的论文则是斯蒂芬·科尔·克莱尼1936年的正规形式定理（Kleene's T predicate）论文[3]:383。
高德纳批评这种转换后的结果类似以下的伪代码，重点是在此转换中完全破坏了原程式的结构[5]:274。Bruce Ian Mills也有类似的看法：“块状结构的精神是其风格，不是使用的语言。利用模拟冯·诺伊曼结构的方式，可以将任何一个面条式代码转换为块状结构的语言，但它面条式代码的本质没有改变。”[6]
p := 1;
while p > 0 do begin
if p = 1 then begin
進行流程圖的步驟1;
p := 流程圖的步驟1之後的步驟編號（若沒有後續步驟，數值為0）;
end;
if p = 2 then begin
進行流程圖的步驟2;
p := 流程圖的步驟2之後的步驟編號（若沒有後續步驟，數值為0）;
end;
...
if p = n then begin
進行流程圖的步驟n;
p := 流程圖的步驟n之後的步驟編號（若沒有後續步驟，數值為0）;
end;
end.
![[icon]](#/media/File:Wiki_letter_w_cropped.svg){kind=small} | 此章节需要扩充。 (2015年5月27日) |
伯姆及贾可皮尼的证明是以流桯图的结构归纳法为基础[3]:381，由于用到图模式匹配，其证明在实务上不能当作是程式转换演算法，因此开创了此一领域的研究[7]。
相关的讨论及研究
因为伯姆及贾可皮尼建构的方式过于复杂，因此此证明没有回答结构化编程是否适用于软体开发的问题，而是引发了后续相关的讨论及争议。在两年之后的1968年，艾兹赫尔·戴克斯特拉就提出著名的“GOTO有害论”[8]。
有些学者试图使伯姆及贾可皮尼的研究结果更加纯粹，因为其论文中没有用到从回圈中间跳出回圈的break及return指令，因此学者认为这是不好的实作方式，学者们鼓励每一个回圈都只能有唯一的结束点，这种设计观点整合到1968至1969年开发的Pascal中。从1969年到1990年代中期，学校常用Pascal来讲授程式语言入门课程[9]。
爱德华·尤登注意到1970年代时在有关是否用自动化方式改写非结构化程式一事，有二元对立的观点，反对者认为需要以结构化程式的方式去思考，而非一味改写，而赞成者的论点是这类的修改实际上可以改善大部份已有的程式[10]。最早提出自动化改写程式概念的有1971年Edward Ashcroft及Zohar Manna的论文[11]。
直接应用伯姆及贾可皮尼定理可能要引入额外的局部变量，也可能产生代码重复的问题[12]，后者也称为loop and a half problem[13]。Pascal受到这些问题的影响，依照埃里克·S·罗伯茨的实验研究，学习程式设计的学生难以用Pascal设计正确程式码来解决简单的问题，其中甚至包括从阵列中找寻一个元素的问题。一篇1980年由Henry Shapiro进行，而后被被罗伯茨引用的研究指出，若只用Pascal提出的流程控制指令，只有20%的人的解答是正确的，但若允许在回圈中直接加入return的话，所有人都写出了正确的答案[9]。
S. Rao Kosaraju在1973年证明只要允许可以从任意深度回圈中多层次跳出，就可以将程式转换成结构化编程，而不用引入额外的变量[1][14]。而且Kosaraju证明了存在一个严格的程式阶层（现在称为Kosaraju阶层），针对任一整数n，存在一个程式，其中包括深度n的多层次跳出，而且在不引入额外变量的条件下，无法用深度小于n的跳出来实现[1]。Kosaraju称这种多层次跳出结构源于BLISS语言。BLISS语言中的多层次跳出形式为leave label，实际上在BLISS-11版本中才引入到BLISS中，原始的BLISS只有单一层次的跳出。BLISS语言家族不提供无限制的跳转指令，Java语言后来也引入类似BLISS语言中的多层次跳出指令[15]:960-965。
Kosaraju的论文中有另一个较简单的结论：若程式可以在不用额外变量（及多层次的跳出）下化约为结构化程式，其充份必要条件是程式中没有一个回圈有二个或二个以上的结束点。简单来说，此处Kosaraju定义的化约是指用相同的“基本动作”及判断，计算相同的函数，但是可能用不同的控制流程（此处的化约比伯姆及贾可皮尼定理中提及的范围要窄）。受到这个结论的启发，Thomas J. McCabe在他引入循环复杂度的论文中的第四部份，描述了对应非结构化程式控制流图（CFG）的Kuratowski定理。使控制流图变得无法结构化的最小子图是：
- 从循环测试以外的地方跳出回圈
- 直接跳跃到回圈中
- 直接跳跃到一个判断分支之中
- 直接跳出一个判断分支
McCabe发现上述这些子图不是彼此独立的，程式无法结构化的充份必要条件是控制流图中有子图有上述四种条件中的三种（或三种以上）。McCabe也发现若非结构化的程式中包括其中四个条件中的一个，它一定还会包含另一个。这也是非结构化的程式流程会纠结到类似义大利面的原因。McCabe也提供一个量化方式，说明一个程式和理想结构化程式之间的距离，并称其为本质复杂度[16]。
到1990年为止，学者们提出许多消除既有程式中跳转指令，但又维持大部份控制架构的方式，也提出许多标示程式等价的方式，这些方式比简单的图灵等价要严格，以免造成类似上述大众定理般的转换结果。这些等价标示的严格程度指定了所需控制流结构的最小集合。1998年Lyle Ramshaw在ACM期刊的论文进行了相关的调查，也提出了自己的方法[17]。Ramshaw的演算法也用在Java反编译器中，因为Java虚拟机有分支指令，以位移来表示分支跳转的目标，但高级的Java语言只有多层次的break及continue指令[18][19][20]。Ammarguellat在1992年提出一种转换方式，回到强制单一结束点的作法[7]。
在Cobol上的应用
 |
1980年代IBM研究员哈伦·米尔斯管理COBOL构建设备（COBOL Structuring Facility）的开发时，将程式的结构化演算法应用到COBOL语言中。[21]。米尔斯的转换方式包括以下的步骤。
- 找出程序中的基础方块。
- 将每一个方块的起始点指定不重复的编号，将每个方块的结束点用所连接方块起始点的编号来标示，程式结束点编号指定为0，程式起始点编号指定为1。
- 将程序分割为基础方块。
- 若某方块的起始点只对应一个方块的结束点，将二个方块合并。
- 定义程序中的一个新的变量，假设为L。
- 针对其他没有合并的结束点，增加一行指令，将L设定为该结束点的编号。
- 将所有基础方块合并成一个选择执行指令，依L的数值执行对应的程式。
- 建立一个回圈，若L不为0，继续执行回圈。
- 建立程序，一开始将L设为1，并开始回圈。
注：将一些选择分支转变为子程序可以改进所得结果。
相关条目
参考资料
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
