洛伦兹力

在电动力学里，劳仑兹力（Lorentz force）是运动于电磁场的带电粒子所感受到的作用力。劳仑兹力是因荷兰物理学者亨德里克·劳仑兹而命名。根据劳仑兹力定律，劳仑兹力可以用方程式，称为劳仑兹力方程式，表达为

${\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )}$；

本条目中，向量与标量分别用粗体与斜体显示。例如，位置向量通常用 ${\displaystyle \mathbf {r} \,\!}$ 表示；而其大小则用 ${\displaystyle r\,\!}$ 来表示。

不同电荷量${\displaystyle q}$的带电粒子，由于磁场${\displaystyle \mathbf {B} }$（磁场方向从屏幕内指出来）的影响，感受到劳仑兹力的作用，所呈现的可能运动轨道。

由于磁场的影响，电子射束的移动路径呈圆形。电子经过的路径会有紫色光发射出来。这是因为电子与玻璃球内的气体分子碰撞而产生的现象。

其中，${\displaystyle \mathbf {F} }$是劳仑兹力，${\displaystyle q}$是带电粒子的电荷量，${\displaystyle \mathbf {E} }$是电场强度，${\displaystyle \mathbf {v} }$是带电粒子的速度，${\displaystyle \mathbf {B} }$是磁感应强度。

劳仑兹力定律是一个基本公理，不是从别的理论推导出来的定律，而是由多次重复完成的实验所得到的同样的结果。

感受到电场的作用，正电荷会朝著电场的方向加速；但是感受到磁场的作用，按照右手定则，正电荷会朝著垂直于速度${\displaystyle \mathbf {v} }$和磁场${\displaystyle \mathbf {B} }$的方向弯曲（详细地说，假设右手的大拇指与${\displaystyle \mathbf {v} }$同向，食指与${\displaystyle \mathbf {B} }$同向，则掌心推出的方向为${\displaystyle \mathbf {F} }$的方向）。

劳仑兹力方程式的${\displaystyle q\mathbf {E} }$项目是电场力项目，${\displaystyle q\mathbf {v} \times \mathbf {B} }$项目是磁场力项目^[1]。处于磁场内的载电导线感受到的磁场力就是这劳仑兹力的磁场力分量。

劳仑兹力方程式的积分形式为

${\displaystyle \mathbf {F} =\int _{\mathbb {V} }(\rho \mathbf {E} +\mathbf {J} \times \mathbf {B} )\ \mathrm {d} \tau }$。

其中，${\displaystyle \mathbb {V} }$是积分的体积，${\displaystyle \rho }$是电荷密度，${\displaystyle \mathbf {J} }$是电流密度，${\displaystyle \mathrm {d} \tau }$是微小体元素。

劳仑兹力密度${\displaystyle \mathbf {f} }$是单位体积的劳仑兹力，表达为：

${\displaystyle \mathbf {f} =\rho \mathbf {E} +\rho \mathbf {v} \times \mathbf {B} =\rho \mathbf {E} +\mathbf {J} \times \mathbf {B} }$。

历史

亨德里克·劳仑兹

1892年，荷兰物理学家亨德里克·劳仑兹提出劳仑兹力的概念^[2]。但是，在劳仑兹之前，就已经有发掘出劳仑兹力方程式的形式，特别是在詹姆斯·马克士威的1861年论文《论物理力线》里的公式（77）：

${\displaystyle P=\mu \gamma {\frac {dy}{dt}}-\mu \beta {\frac {dz}{dt}}+{\frac {dF}{dt}}-{\frac {d\Psi }{dx}}}$、

${\displaystyle Q=\mu \alpha {\frac {dz}{dt}}-\mu \gamma {\frac {dx}{dt}}+{\frac {dG}{dt}}-{\frac {d\Psi }{dy}}}$、

${\displaystyle R=\mu \beta {\frac {dx}{dt}}-\mu \alpha {\frac {dy}{dt}}+{\frac {dH}{dt}}-{\frac {d\Psi }{dz}}}$；

其中，${\displaystyle P}$、${\displaystyle Q}$、${\displaystyle R}$分别为电场的三个分量，${\displaystyle \mu }$是磁导率，${\displaystyle {\frac {dx}{dt}}}$、${\displaystyle {\frac {dy}{dt}}}$、${\displaystyle {\frac {dz}{dt}}}$分别为导电体的移动速度的三个分量，${\displaystyle \alpha }$、${\displaystyle \beta }$、${\displaystyle \gamma }$分别为磁场强度的三个分量，${\displaystyle F}$、${\displaystyle G}$、${\displaystyle H}$分别为磁矢势的三个分量，${\displaystyle \Psi }$是电势。

后来，在他的1864年论文《电磁场的动力学理论》里，马克士威将这公式列为马克士威方程组的八个原本方程式中的方程式（D）:

${\displaystyle \mathbf {E} =\mathbf {v} \times (\mu \mathbf {H} )-{\frac {\partial \mathbf {A} }{\partial t}}-\nabla \phi }$；

其中，${\displaystyle \mathbf {v} }$是速度，${\displaystyle \mathbf {H} }$是磁场强度，${\displaystyle \mu }$是磁导率，${\displaystyle \mathbf {A} }$是磁矢势，${\displaystyle \phi }$是电势。

很明显地，马克士威版是现代版的前导。两个版本的差别为：

• 马克士威版并没有特意地提到电荷。马克士威称物理量${\displaystyle \mathbf {E} }$为电动力（electromotive force）。这英文原文与电动势的英文原文相同。很多物理学家都对英文原文表示意见，认为会造成困惑，是个相当不精确的术语。从方程式形式和单位分析方面来看，这物理量对应于现代的物理量单位电荷的劳仑兹力。
• 马克士威版包含有现在称为电场的项目，以电势${\displaystyle \phi }$和磁向量势${\displaystyle \mathbf {A} }$来表达：

${\displaystyle \mathbf {E} =-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}}$。

取旋度于这表达式，就可以得到法拉第-马克士威方程式^[1]：

${\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}$。

因此，这表达式等价于法拉第-马克士威方程式。尽管劳仑兹力方程式来自于原本的一条马克士威方程式，现在，经过奥利弗·黑维塞重新表述后的劳仑兹力方程式，不再被视为马克士威方程组中的一员，而成为伴随马克士威方程组的一条独立基要的定律。

劳仑兹力定律的重要意义

当马克士威方程组描绘带电粒子怎样产生电磁场的同时，劳仑兹力方程式描绘了移动于电磁场的带电粒子所感受到的电磁力。这使得整个电磁动力的图画得以完整。在一个复杂的物理系统里，带电粒子可能还会感受到别种作用力，像万有引力或核力。马克士威方程组并非与这些作用力完全无关；而是通过带电粒子或电流密度与这些作用力耦合。

对于实际的物质，在原则上和计算的复杂程度上，劳仑兹力方程式都不足以描述一群粒子的物理行为。在物质介质里的带电粒子，必须同时地响应和生成电磁场。除此以外，还必须考虑到描述这一群粒子的运动的传输方程式，例如，波兹曼传输方程式（Boltzmann equation）、福克-普朗克方程式^[3]（Fokker–Planck equation）、纳维-斯托克斯方程式、等等。请参阅磁流体力学、超导现象、恒星演化、等等。在这些学术领域研究的科学家必须解析复杂的传输方程式，求得带电粒子在时间和空间方面的响应。

或许有些读者会认为这些理论只是靠著近似来处理一个大系综的带电粒子。从更深的层面来看，带电粒子也会对非电磁力，像万有引力，核力或边界条件等等，产生响应。

粒子的运动轨道

给予作用于粒子的劳仑兹力的公式，将这公式代入牛顿第二运动定律，可以得到粒子的运动方程式。解析这运动方程式，就可以找到粒子的运动轨道。

范例：回旋加速器

移动于均匀磁场${\displaystyle \mathbf {B} }$（从显示萤幕外，指入显示萤幕），正电荷的圆周运动轨道。

在一个简单的回旋加速器内，均匀磁场是${\displaystyle \mathbf {B} =B_{0}{\hat {\mathbf {z} }}}$，电场是零。那么，运动于xy-平面的带电粒子${\displaystyle q}$所感受到的劳仑兹力${\displaystyle \mathbf {F} }$为

${\displaystyle \mathbf {F} =q\mathbf {v} \times \mathbf {B} }$。

将这公式代入牛顿第二运动定律，

${\displaystyle m\mathbf {a} =q\mathbf {v} \times \mathbf {B} }$；

其中，${\displaystyle m}$是带电粒子的质量，${\displaystyle \mathbf {a} }$是带电粒子的加速度。

由于带电粒子的加速度与速度互相垂直，带电粒子呈圆周运动。假设粒子带有正电荷，则这公式的一般解答为

${\displaystyle \mathbf {r} =r_{c}(\cos \omega t,\,-\sin \omega t,\,0)}$；

其中，${\displaystyle \mathbf {r} }$是带电粒子的圆周运动轨道，${\displaystyle r_{c}}$是圆周半径，${\displaystyle \omega =qB/m}$是旋转角速度，${\displaystyle t}$是时间。

移动于朝著正上方的均匀磁场，负电荷的等速螺旋运动轨道。

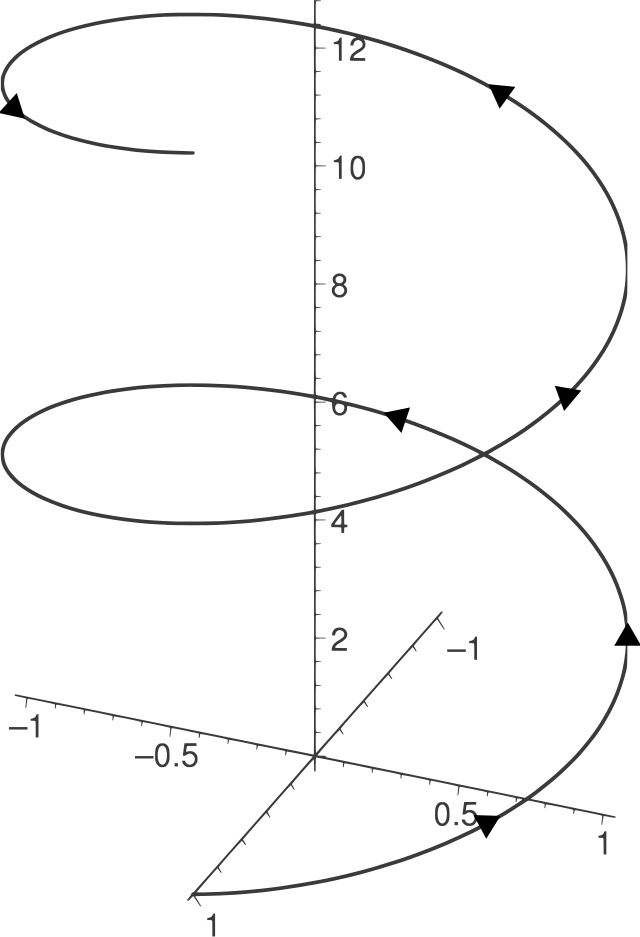
朝著均匀磁场方向看，带电粒子会以反时针方向，呈等速圆周运动。给予初始速率${\displaystyle v_{0}}$。那么，圆周半径为

${\displaystyle r_{c}=v_{0}/\omega =mv_{0}/qB}$。

这圆周半径称为回旋半径（cyclotron radius）或拉莫半径（Larmor radius）。${\displaystyle \omega =qB/m}$称为回旋频率（cyclotron frequency）。

带电粒子的动量${\displaystyle p_{0}}$为

${\displaystyle p_{0}=mv_{0}=qBr_{c}}$。

假设粒子带有负电荷，则运动方向会逆反，改为顺时针方向。

假设初始速度有一个z-分量${\displaystyle v_{z0}}$，则带电粒子会呈等速螺旋运动。

导向中心漂移运动

主条目：导向中心

在均匀磁场内，带电粒子的漂移运动。（A）没有任何外力（B）加入外电场${\displaystyle \mathbf {E} }$（C）加入独立外力${\displaystyle \mathbf {F} }$（例如，地心引力，（D））磁场改为不均匀，${\displaystyle \nabla \mathbf {B} }$

对于很多有意思的、比较复杂的实际案例，在磁场内运动的带电粒子（例如，电浆的电子或离子），可以分为两部分处理。这两部分的叠加，足以描述这带电粒子的物理行为。第一部分是速度比较快的，环绕著某一点的圆周运动。环绕之点称为导向中心（guiding center）。另一部分是导向中心的漂移运动。其速度比较慢，会因不同种类的粒子而不同，又跟其电荷量、质量或温度有关。不同的漂移速度可能会造成电流或化学分离。

电场和磁场的定义

许多经典电磁学教科书会用劳仑兹力定律来定义电场和磁场。

电场

假设检验电荷静止不动，${\displaystyle \mathbf {v} =0}$，则劳仑兹力方程式变为

${\displaystyle \mathbf {F} =q\mathbf {E} }$。

采用国际单位制，假设检验电荷的电量为1库仑，作用于检验电荷的劳伦兹力为1牛顿，则检验电荷感受到的电场为1牛顿／库仑。

磁场

假设电场为零，则作用于电荷${\displaystyle q}$的劳仑兹力是

${\displaystyle \mathbf {F} =q\mathbf {v} \times \mathbf {B} }$。

对于一条线电荷密度为${\displaystyle \lambda }$的载流导线，总作用力为

${\displaystyle \mathbf {F} =\int _{\mathbb {C} }\mathbf {v} \times \mathbf {B} \mathrm {d} q=\int _{\mathbb {C} }\mathbf {v} \times \mathbf {B} \lambda \mathrm {d} \ell =\int _{\mathbb {C} }\mathbf {I} \times \mathbf {B} \mathrm {d} \ell }$；

其中，${\displaystyle \mathbb {C} }$是积分路径，${\displaystyle \mathbf {I} =\lambda \mathbf {v} }$是电流向量。

假设电流是稳定电流，则可以将电流从积分内提出，用向量${\displaystyle \mathrm {d} {\boldsymbol {\ell }}}$来表示电流${\displaystyle \mathbf {I} }$的方向：

${\displaystyle \mathbf {F} =I\int _{\mathbb {C} }\mathrm {d} {\boldsymbol {\ell }}\times \mathbf {B} }$。

这公式给出了，在磁场内，载流导线感受到的磁场力。

使用这公式和必欧-沙伐定律，就可以推导出安培力定律（详尽细节，请参阅安培力定律）。

假设，磁场是均匀磁场，积分路径是垂直于磁场的直线，则

${\displaystyle F=ILB}$；

其中，${\displaystyle L}$是积分路径${\displaystyle \mathbb {C} }$的长度，

采用国际单位制，假设检验电流为1安培，作用于载流导线的单位长度的劳仑兹力为1牛顿/公尺，则检验电流感受到的磁场为1特斯拉。

动生电动势

一条长度为${\displaystyle L}$的细直导线以速度${\displaystyle \mathbf {v} }$移动于磁场${\displaystyle \mathbf {B} }$。

许多发电机的基本运作原理涉及动生电动势概念。将导线移动于磁场，则会产生电动势，称为动生电动势。如图右^[4]，假设一条长度为${\displaystyle L}$的细直导线，以速度${\displaystyle \mathbf {v} }$移动于磁场${\displaystyle \mathbf {B} }$。磁场${\displaystyle \mathbf {B} }$以箭尾或叉叉表示，方向由银幕外部指入银幕。思考在这导线内的电荷${\displaystyle q}$，根据劳仑兹定律，会感受到劳仑兹力${\displaystyle \mathbf {F} _{lorentz}}$：

${\displaystyle \mathbf {F} _{lorentz}=q\mathbf {v} \times \mathbf {B} }$。

在这里，劳仑兹力也是磁场力。因为这磁场力的作用，正电荷会往导线的上端移动，负电荷会往导线的下端移动。在稳定平衡状态，这会感应出一个电场${\displaystyle \mathbf {E} }$：

${\displaystyle \mathbf {E} =-\mathbf {v} \times \mathbf {B} }$。

电动势定义为造成开路电路的两个终端的电势差，对于每单位电荷所需做的功。所以，动生电动势${\displaystyle {\mathcal {E}}}$为

${\displaystyle {\mathcal {E}}=\int _{L}{\frac {\mathbf {F_{lorentz}} }{q}}\cdot d{\boldsymbol {\ell }}=vBL}$。

在这个例子里，稳定平衡状态时的电流等于零。假设载流导线与其他原件连结成一个电路，则会因为动生电动势而产生电流。例如，将一个电阻${\displaystyle R}$与导线的两端相连结，则流过电阻的电流${\displaystyle I}$为

${\displaystyle I={\mathcal {E}}/R=vBL/R}$。

法拉第电磁感应定律

在时间${\displaystyle t}$，以闭回路${\displaystyle \partial \Sigma (t)}$为边缘的曲面${\displaystyle \Sigma (t)}$，和在此曲面${\displaystyle \Sigma (t)}$某些位置的磁场${\displaystyle \mathbf {B} (\mathbf {r} ,\,t)}$。

一个以常速度${\displaystyle \mathbf {v} }$移动于磁场${\displaystyle \mathbf {B} (\mathbf {r} ,\,t)}$的闭回路${\displaystyle \partial \Sigma (t)}$。

主条目：法拉第电磁感应定律

法拉第电磁感应定律阐明，穿过任意闭回路的磁通量的变化率，与这回路的电动势成正比：

${\displaystyle {\mathcal {E}}=-{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}}$；

其中，${\displaystyle {\mathcal {E}}}$是电动势，${\displaystyle \Phi _{B}}$是磁通量，${\displaystyle t}$是时间。

在时间${\displaystyle t}$通过任意曲面${\displaystyle \Sigma (t)}$的磁通量${\displaystyle \Phi _{B}(t)}$定义为

${\displaystyle \Phi _{B}(t)\ {\stackrel {def}{=}}\ \int _{\Sigma (t)}\mathbf {B} (\mathbf {r} ,\,t)\cdot d\mathbf {a} }$；

其中，${\displaystyle \mathbf {r} }$是位置，${\displaystyle d\mathbf {a} }$是微小面元素。

给予一个以常速度${\displaystyle \mathbf {v} }$移动于磁场的闭回路${\displaystyle \partial \Sigma (t)}$。那么，磁通量对于时间的全微分是^[5]

${\displaystyle {\begin{aligned}d\Phi _{B}(t)&=\int _{\Sigma (t+dt)}\mathbf {B} (\mathbf {r} ,\,t+dt)\cdot d\mathbf {a} -\int _{\Sigma (t)}\mathbf {B} (\mathbf {r} ,\,t)\cdot d\mathbf {a} \\&=\int _{\Sigma (t+dt)}\mathbf {B} (\mathbf {r} ,\,t)\cdot d\mathbf {a} +\int _{\Sigma (t+dt)}{\frac {\partial \mathbf {B} (\mathbf {r} ,\,t)}{\partial t}}dt\cdot d\mathbf {a} -\int _{\Sigma (t)}\mathbf {B} (\mathbf {r} ,\,t)\cdot d\mathbf {a} \\&=\int _{\Sigma (t+dt)}{\frac {\partial \mathbf {B} (\mathbf {r} ,\,t)}{\partial t}}dt\cdot d\mathbf {a} +\int _{\Sigma _{total}}\mathbf {B} (\mathbf {r} ,\,t)\cdot d\mathbf {a} -\int _{\Sigma _{ribbon}}\mathbf {B} (\mathbf {r} ,\,t)\cdot d\mathbf {a} \\\end{aligned}}}$ ；

其中，${\displaystyle \Sigma (t)}$是边缘为${\displaystyle \partial \Sigma (t)}$的曲面，${\displaystyle \Sigma _{total}}$是包括${\displaystyle \Sigma (t+dt)}$、${\displaystyle -\Sigma (t)}$和${\displaystyle \Sigma _{ribbon}}$的闭曲面，${\displaystyle \Sigma _{ribbon}}$是边缘${\displaystyle \partial \Sigma (t+dt)}$和${\displaystyle \partial \Sigma (t)}$形成的边缘曲面。

根据散度定理和高斯磁定律，

${\displaystyle \int _{\Sigma _{total}}\mathbf {B} \cdot d\mathbf {a} =\int _{\mathbb {V} _{total}}\nabla \cdot \mathbf {B} d\tau =0}$；

其中，${\displaystyle \mathbb {V} _{total}}$是闭曲面${\displaystyle \Sigma _{total}}$包含的空间，${\displaystyle d\tau }$是微小体元素。

通过边缘曲面${\displaystyle \Sigma _{ribbon}}$的磁通量可以改变成一个线积分：

${\displaystyle \int _{\Sigma _{ribbon}}\mathbf {B} \cdot d\mathbf {a} =\int _{\partial \Sigma (t)}\mathbf {B} \cdot [d{\boldsymbol {\ell }}\times (\mathbf {v} dt)]=\int _{\partial \Sigma (t)}[(\mathbf {v} dt)\times \mathbf {B} ]\cdot d{\boldsymbol {\ell }}}$。

所以，磁通量对于时间的全导数，或磁通量的变化率为

${\displaystyle {\frac {d\Phi _{B}(t)}{dt}}=\int _{\Sigma (t+dt)}{\frac {\partial \mathbf {B} (\mathbf {r} ,\,t)}{\partial t}}\cdot d\mathbf {a} -\int _{\partial \Sigma (t)}\mathbf {v} \times \mathbf {B} \cdot d{\boldsymbol {\ell }}}$。

运动于移动的闭回路${\displaystyle \partial \Sigma (t)}$的一个电荷${\displaystyle q}$的速度${\displaystyle \mathbf {w} }$为

${\displaystyle \mathbf {w} =\mathbf {u} +\mathbf {v} }$；

其中，${\displaystyle \mathbf {u} }$是相对于闭回路${\displaystyle \partial \Sigma (t)}$的电荷运动速度，${\displaystyle \mathbf {v} }$是闭回路${\displaystyle \partial \Sigma (t)}$的移动速度。

这电荷会感受到劳仑兹力

${\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {w} \times \mathbf {B} )}$；

电动势${\displaystyle {\mathcal {E}}}$定义为

${\displaystyle {\mathcal {E}}\ {\stackrel {def}{=}}\ \int _{\partial \Sigma }{\frac {\mathbf {F} }{q}}\cdot d{\boldsymbol {\ell }}=\int _{\partial \Sigma }(\mathbf {E} +\mathbf {w} \times \mathbf {B} )\cdot d{\boldsymbol {\ell }}}$。

根据法拉第电磁感应定律，

${\displaystyle {\mathcal {E}}=-{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}=\int _{\partial \Sigma }(\mathbf {E} +\mathbf {w} \times \mathbf {B} )\cdot d{\boldsymbol {\ell }}}$。

在计算积分时，闭回路${\displaystyle \partial \Sigma (t)}$的微小线元素${\displaystyle d{\boldsymbol {\ell }}}$与正在那位置的电荷的${\displaystyle \mathbf {u} }$平行。所以，

${\displaystyle {\frac {d\Phi _{B}(t)}{dt}}=-\int _{\partial \Sigma }(\mathbf {E} +\mathbf {v} \times \mathbf {B} )\cdot d{\boldsymbol {\ell }}}$。

令两个磁通量变化率的方程式相等，除去同有的移动的闭回路项目，则可得到

${\displaystyle \int _{\partial \Sigma }\mathbf {E} \cdot d{\boldsymbol {\ell }}=-\int _{\Sigma }{\frac {\partial \mathbf {B} }{\partial t}}\cdot d\mathbf {a} }$。

应用斯托克斯定理，${\displaystyle \int _{\partial \Sigma }\mathbf {E} \cdot d{\boldsymbol {\ell }}=\int _{\Sigma }\nabla \times \mathbf {E} \cdot d\mathbf {a} }$，可以得到

${\displaystyle \int _{\Sigma }\left(\nabla \times \mathbf {E} +{\frac {\partial \mathbf {B} }{\partial t}}\right)\cdot d\mathbf {a} =0}$。

由于${\displaystyle \Sigma }$是任意取面，可以将被积式从积分中取出：

${\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}$。

这是马克士威-法拉第方程式。由于这方程式的右手边是个对于时间的偏导数项目，只涉及固定的闭回路，不能用来计算移动中的闭回路。

用马克士威-法拉第方程式，通常对于时间的偏导数的诠释只限制为固定边界。而在另一方面，不论导线的闭回路是刚硬固定的、是在运动中、是在形变过程中，不论磁场是不含时的或含时的，法拉第电磁感应定律都成立。但是，对于某些案例，法拉第电磁感应定律并不适用或使用起来很困难。这时候，必须使用劳仑兹力定律。详尽细节，请参阅法拉第电磁感应定律不适用案例。

假设闭回路移动于不含时间的磁场${\displaystyle \mathbf {B} }$，通过闭回路的磁通量${\displaystyle \Phi _{B}}$会因为几种因素而改变：例如，假若磁场${\displaystyle \mathbf {B} }$随著位置改变，闭回路移动至不同磁场${\displaystyle \mathbf {B} }$的位置，则磁通量${\displaystyle \Phi _{B}}$会改变。或者，假若相对于磁场，闭回路的定向改变，由于微小元素${\displaystyle \mathbf {B} \cdot d\mathbf {A} }$的改变，磁通量${\displaystyle \Phi _{B}}$也会改变。再举一个例子，假若闭回路扫掠过一个均匀的不含时磁场，由于闭回路的形变，磁通量${\displaystyle \Phi _{B}}$会改变。对于这三个案例，法拉第电磁感应定律正确地计算出磁通量变化率${\displaystyle {\frac {d\Phi _{B}}{dt}}}$所产生的电动势。

对比前面所述状况，假设固定的闭回路处于含时磁场${\displaystyle \mathbf {B} }$，马克士威-法拉第方程式会显示出一个非保守性的电场${\displaystyle \mathbf {E} }$产生于闭回路，靠著劳仑兹力的${\displaystyle q\mathbf {E} }$项目，驱使载电粒子移动于导线。这状况也会改变磁通量${\displaystyle \Phi _{B}}$，法拉第电磁感应定律也会正确地计算出磁通量变化率${\displaystyle {\frac {d\Phi _{B}}{dt}}}$所产生的电动势。

用位势来表达劳仑兹力方程式

参见：电磁场的数学表述、麦克斯韦方程组和亥姆霍兹分解

根据亥姆霍兹分解（Helmholtz decomposition），电场和磁场可以用电势${\displaystyle \phi }$和磁向量势${\displaystyle \mathbf {A} }$来表达：

${\displaystyle \mathbf {E} =-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}}$

${\displaystyle \mathbf {B} =\nabla \times \mathbf {A} }$

其中∇为梯度，∇⋅ 为散度，∇× 为旋度。

将这两个公式代入劳仑兹力方程式，则可得到

${\displaystyle \mathbf {F} =q\left[-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}+\mathbf {v} \times (\nabla \times \mathbf {A} )\right]}$

可以化简为

${\displaystyle \mathbf {F} =q\left[-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}+\nabla (\mathbf {v} \cdot \mathbf {A} )-(\mathbf {v} \cdot \nabla )\mathbf {A} \right]}$

劳仑兹力方程式的协变形式

定义粒子的四维速度${\displaystyle u_{\beta }}$为

${\displaystyle u_{\beta }\ {\stackrel {def}{=}}\ (u_{0},\,u_{1},\,u_{2},\,u_{3})=\gamma (c,\,-v_{x},\,-v_{y},\,-v_{z})}$；

其中，${\displaystyle \gamma }$是劳仑兹因子，${\displaystyle c}$是光速，${\displaystyle \mathbf {v} =(v_{x},\,v_{y},\,v_{z})}$是粒子的速度向量。

定义电磁场张量${\displaystyle F^{\alpha \beta }}$为

${\displaystyle F^{\alpha \beta }\ {\stackrel {def}{=}}\ {\begin{bmatrix}0&-E_{x}/c&-E_{y}/c&-E_{z}/c\\E_{x}/c&0&-B_{z}&B_{y}\\E_{y}/c&B_{z}&0&-B_{x}\\E_{z}/c&-B_{y}&B_{x}&0\end{bmatrix}}}$；

其中，${\displaystyle \mathbf {E} }$是电场向量，${\displaystyle \mathbf {B} }$是磁场向量。

结合牛顿运动定律与劳仑兹力定律在一起，以电磁场张量写为反变形式（contravariant form）：

${\displaystyle {\frac {dp^{\alpha }}{d\tau }}=qu_{\beta }F^{\alpha \beta }}$；

其中，${\displaystyle p^{\alpha }}$是四维动量，${\displaystyle \tau }$是粒子的固有时。

应用劳仑兹变换，电磁场张量可以从一个参考系${\displaystyle S}$转换到另一个参考系${\displaystyle {\bar {S}}}$：

${\displaystyle {\bar {F}}^{\mu \nu }={\Lambda ^{\mu }}_{\alpha }{\Lambda ^{\nu }}_{\beta }F^{\alpha \beta }}$；

其中，${\displaystyle {\Lambda ^{\mu }}_{\alpha }}$和${\displaystyle {\Lambda ^{\nu }}_{\beta }}$是劳仑兹变换矩阵。

换另一种方法，定义四维势${\displaystyle A^{\alpha }}$为

${\displaystyle A^{\alpha }\ {\stackrel {def}{=}}\ (\phi /c,\,A_{x},\,A_{y},\,A_{z})}$；

其中，${\displaystyle \phi }$是电势，${\displaystyle \mathbf {A} }$是磁向量势。

定义四维坐标 ${\displaystyle x_{\alpha }}$为

${\displaystyle x_{\alpha }\ {\stackrel {def}{=}}\ (ct,\,-x,\,-y,\,-z)}$。

那么，电磁场张量为^[1]

${\displaystyle F^{\alpha \beta }={\frac {\partial A^{\beta }}{\partial x_{\alpha }}}-{\frac {\partial A^{\alpha }}{\partial x_{\beta }}}}$。

从劳仑兹力方程式的张量形式计算向量形式

先计算四维力（four-force）的${\displaystyle \mu =1}$分量（x-分量）：

${\displaystyle \gamma {\frac {dp^{1}}{dt}}={\frac {dp^{1}}{d\tau }}=qu_{\beta }F^{1\beta }=q\left(u_{0}F^{10}+u_{1}F^{11}+u_{2}F^{12}+u_{3}F^{13}\right)}$。

将电磁场张量的分量代入，可以得到

${\displaystyle \gamma {\frac {dp^{1}}{dt}}=q\left(u_{0}\left({\frac {E_{x}}{c}}\right)+u_{2}(-B_{z})+u_{3}(B_{y})\right)}$。

再将四维速度的分量代入，则会得到

${\displaystyle \gamma {\frac {dp^{1}}{dt}}=q\gamma \left(c\left({\frac {E_{x}}{c}}\right)+v_{y}B_{z}-v_{z}B_{y}\right)=q\gamma [E_{x}+(\mathbf {v} \times \mathbf {B} )_{x}]}$。

类似地，可以计算出四维力的${\displaystyle \mu =2}$和${\displaystyle \mu =3}$分量。所以，

${\displaystyle {\frac {d\mathbf {p} }{dt}}=q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )}$。

参阅

回旋加速器 质谱仪 电动机 移动中的磁铁与导体问题

磁轨炮 发电机 直线电动机

霍尔效应 阿布拉罕-劳仑兹力 磁流体力学

参考文献

1. Griffiths, David J. Introduction to Electrodynamics (3rd ed.). Prentice Hall. 1998: pp. 204, 326, 417, 541. ISBN 0-13-805326-X. 引文格式1维护：冗余文本 (link)
2. Darrigol, Olivier, Electrodynamics from Ampère to Einstein, Oxford, [England]: Oxford University Press: 327, 2000, ISBN 0-198-50593-0
3. 福克-普朗克方程. 维基百科，自由的百科全书. 2015-12-13 （中文）.
4. Tai L. Chow. Electromagnetic theory. Sudbury MA: Jones and Bartlett. 2006: pp. 172-175. ISBN 0-7637-3827-1. 引文格式1维护：冗余文本 (link)
5. Flanders, Harley. Differentiation under the integral sign. American Mathematical Monthly. Jun–Jul 1973, 80 (6): 615–627. doi:10.2307/2319163.

外部链接

• National High Magnetic Field Laboratory的Java互动教学网页：劳仑兹力。