抛物线座标系

抛物线坐标系（英语：Parabolic coordinates）是一种二维正交坐标系，两个坐标的等值曲线都是共焦的抛物线。将二维的抛物线坐标系绕著抛物线的对称轴旋转，则可以得到三维的抛物线坐标系。

抛物线坐标系的绿色的 ${\displaystyle \sigma }$ 等值曲线和红色的 ${\displaystyle \tau }$ 等值曲线。横轴与纵轴分别为 x-轴与 y-轴。

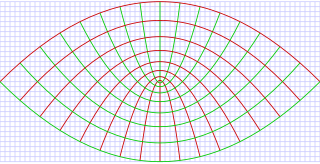
实际上，抛物线坐标可以应用在许多物理问题。例如，斯塔克效应（Stark effect），物体边缘的位势论，以及拉普拉斯-龙格-冷次向量的保守性。

二维抛物线坐标系

直角坐标 ${\displaystyle (x,\ y)}$ 可以用二维抛物线坐标 ${\displaystyle (\sigma ,\ \tau )}$ 表示为

${\displaystyle x=\pm \,\sigma \tau }$ 、

${\displaystyle y={\frac {1}{2}}\left(\tau ^{2}-\sigma ^{2}\right)}$ ；

其中，${\displaystyle \sigma \geq 0}$ ，${\displaystyle \tau \geq 0}$ 。

反算回来，二维抛物线坐标 ${\displaystyle (\sigma ,\ \tau )}$ 可以用直角坐标 ${\displaystyle (x,\ y)}$ 表示为

${\displaystyle \sigma ={\sqrt {-y+{\sqrt {x^{2}+y^{2}}}}}}$ 、

${\displaystyle \tau ={\sqrt {y+{\sqrt {x^{2}+y^{2}}}}}}$ 。

坐标 ${\displaystyle \sigma }$ 为常数的曲线形成共焦的，凹性向上的（往 +y-轴）抛物线：

${\displaystyle 2y={\frac {x^{2}}{\sigma ^{2}}}-\sigma ^{2}}$ ，

而坐标 ${\displaystyle \tau }$ 为常数的曲线形成共焦的，凹性向下的（往 -y-轴）抛物线：

${\displaystyle 2y=-{\frac {x^{2}}{\tau ^{2}}}+\tau ^{2}}$ 。

这些抛物线的焦点的位置都在原点。

二维标度因子

抛物线坐标 ${\displaystyle (\sigma ,\ \tau )}$ 的标度因子相等：

${\displaystyle h_{\sigma }=h_{\tau }={\sqrt {\sigma ^{2}+\tau ^{2}}}}$ 。

因此，面积的无穷小元素是

${\displaystyle dA=\left(\sigma ^{2}+\tau ^{2}\right)d\sigma d\tau }$ 。

拉普拉斯算子是

${\displaystyle \nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left({\frac {\partial ^{2}\Phi }{\partial \sigma ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \tau ^{2}}}\right)}$ 。

其它微分算子，像 ${\displaystyle \nabla \cdot \mathbf {F} }$ ， ${\displaystyle \nabla \times \mathbf {F} }$ ，都可以用 ${\displaystyle (\sigma ,\ \tau )}$ 坐标表示，只要将标度因子代入在正交坐标系条目内的一般公式。

三维抛物线坐标系

三维抛物线坐标的坐标曲面。红色的抛物曲面的坐标 ${\displaystyle \tau =2}$ 。蓝色的抛物曲面的坐标 ${\displaystyle \sigma =1}$ 。黄色的半平面的坐标 ${\displaystyle \phi =-60^{\circ }}$ 。三个面相交于点 ${\displaystyle \mathbf {P} =(1.0,-1.732,1.5)}$ （以黑色小球表示）。

将二维的抛物线坐标系绕著抛物线的对称轴旋转，则可以得到三维的抛物线坐标系，又称为旋转抛物线坐标系。将对称轴与 z-轴排列成同直线；而抛物线坐标系的共焦点与直角坐标系的原点同地点。直角坐标 ${\displaystyle (x,\ y,\ z)}$ 可以用三维抛物线坐标 ${\displaystyle (\sigma ,\ \tau ,\ \phi )}$ 表示为

${\displaystyle x=\sigma \tau \cos \phi }$ 、

${\displaystyle y=\sigma \tau \sin \phi }$ 、

${\displaystyle z={\frac {1}{2}}\left(\tau ^{2}-\sigma ^{2}\right)}$ ；

其中，${\displaystyle \sigma \geq 0}$ ，${\displaystyle \tau \geq 0}$ ，方位角 ${\displaystyle \phi }$ 定义为

${\displaystyle \tan \phi ={\frac {y}{x}},\qquad 0\leq \phi \leq 2\pi }$ 。

反算回来，三维抛物线坐标 ${\displaystyle (\sigma ,\ \tau ,\ \phi )}$ 可以用直角坐标 ${\displaystyle (x,\ y,\ z)}$ 表示为

${\displaystyle \sigma ={\sqrt {-z+{\sqrt {x^{2}+y^{2}+z^{2}}}}}}$ 、

${\displaystyle \tau ={\sqrt {z+{\sqrt {x^{2}+y^{2}+z^{2}}}}}}$ 、

${\displaystyle \phi =\tan ^{-1}{\frac {y}{x}}}$ 。

每一个 ${\displaystyle \sigma }$-坐标曲面都是共焦的，凹性向上的（往 +z-轴）抛物曲面：

${\displaystyle 2z={\frac {x^{2}+y^{2}}{\sigma ^{2}}}-\sigma ^{2}}$ ，

而每一个 ${\displaystyle \tau }$>-坐标曲面都是共焦的，凹性向下的（往 -z-轴）抛物曲面：

${\displaystyle 2z=-{\frac {x^{2}+y^{2}}{\tau ^{2}}}+\tau ^{2}}$ 。

这些抛物曲面的焦点的位置都在原点。

三维标度因子

三维标度因子为：

${\displaystyle h_{\sigma }={\sqrt {\sigma ^{2}+\tau ^{2}}}}$ 、

${\displaystyle h_{\tau }={\sqrt {\sigma ^{2}+\tau ^{2}}}}$ 、

${\displaystyle h_{\phi }=\sigma \tau \,}$ 。

我们可以观察出，标度因子 ${\displaystyle h_{\sigma }}$ ， ${\displaystyle h_{\tau }}$ 与二维标度因子相同。因此，体积的无穷小元素是

${\displaystyle dV=h_{\sigma }h_{\tau }h_{\phi }=\sigma \tau \left(\sigma ^{2}+\tau ^{2}\right)\,d\sigma \,d\tau \,d\phi }$ 。

拉普拉斯算子是

${\displaystyle \nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left[{\frac {1}{\sigma }}{\frac {\partial }{\partial \sigma }}\left(\sigma {\frac {\partial \Phi }{\partial \sigma }}\right)+{\frac {1}{\tau }}{\frac {\partial }{\partial \tau }}\left(\tau {\frac {\partial \Phi }{\partial \tau }}\right)\right]+{\frac {1}{\sigma ^{2}\tau ^{2}}}{\frac {\partial ^{2}\Phi }{\partial \phi ^{2}}}}$ 。

其它微分算子，像 ${\displaystyle \nabla \cdot \mathbf {F} }$ ， ${\displaystyle \nabla \times \mathbf {F} }$ ，都可以用 ${\displaystyle (\sigma ,\ \tau ,\ \phi )}$ 坐标表示，只要将标度因子代入在正交坐标系 条目内的一般公式。

第二种表述

另外还有一种抛物线坐标系的表述，专门用于哈密顿-亚可比方程式。假若使用此种表述的公式，则哈密顿-亚可比方程式可以很容易的分解出来。应用此方法，可以导引出拉普拉斯-龙格-冷次向量的恒定性．

采用下述从抛物线坐标变换至直角坐标的公式：

${\displaystyle \eta ={-z+{\sqrt {x^{2}+y^{2}+z^{2}}}}}$ 、

${\displaystyle \xi ={z+{\sqrt {x^{2}+y^{2}+z^{2}}}}}$ 、

${\displaystyle \phi =\arctan {y \over x}}$ 。

假若 ${\displaystyle \phi =0}$ ，则可得到一片截面；其坐标被限制于 ${\displaystyle x\geq 0}$ 的 +xz-半平面：

${\displaystyle \eta =-z+{\sqrt {x^{2}+z^{2}}}}$ 、

${\displaystyle \xi =z+{\sqrt {x^{2}+z^{2}}}}$ 。

假若包含于一条曲线的每一点的坐标 ${\displaystyle \eta }$ 是一个常数，${\displaystyle \eta =c}$ ，则

${\displaystyle \left.z\right|_{\eta =c}={x^{2} \over 2c}-{c \over 2}}$ 。

这是一个共焦点在原点的抛物线；对称轴与 z-轴同轴；凹性向上。

假若包含于一条曲线的每一点的坐标 ${\displaystyle \xi }$ 是一个常数，${\displaystyle \xi =b}$ ，则

${\displaystyle \left.z\right|_{\xi =b}={b \over 2}-{x^{2} \over 2b}}$ 。

这也是一个共焦点在原点的抛物线；对称轴与 z-轴同轴；凹性向下。

思考任何一条向上的抛物线 ${\displaystyle \eta =c}$ 与任何一条向下的抛物线 ${\displaystyle \xi =b}$ ，我们想要求得两条曲线的相交点：

${\displaystyle {x^{2} \over 2c}-{c \over 2}={b \over 2}-{x^{2} \over 2b}}$ 。

稍微计算，可得

${\displaystyle x={\sqrt {bc}}}$ 。

将相交点的横坐标 ${\displaystyle x}$ 代入向上的抛物线的公式，

${\displaystyle z_{c}={bc \over 2c}-{c \over 2}={b-c \over 2}}$ 。

所以，相交点 P 坐标为 ${\displaystyle \left({\sqrt {bc}},\ {b-c \over 2}\right)}$ 。

思考正切这两条抛物线于点 P 的一对切线。向上的抛物线的切线的斜率为

${\displaystyle {\frac {dz_{c}}{dx}}={\frac {x}{c}}={\sqrt {\frac {b}{c}}}=s_{c}}$ 。

向下的抛物线的切线的斜率为

${\displaystyle {dz_{b} \over dx}=-{x \over b}=-{\sqrt {c \over b}}=s_{b}}$ 。

两个斜率的乘积为

${\displaystyle s_{c}s_{b}=-1}$ 。

所以，两条切线相垂直。对于任何两条凹性相反的抛物线，都会有同样的结果。

假设 ${\displaystyle \phi \neq 0}$ 。让 ${\displaystyle \phi }$ 值从 ${\displaystyle 0}$ 缓慢增值，这半平面会相应地绕著 z-轴按照右手定则旋转；抛物线坐标为常数的抛物线 形成了抛物曲面。一对相反的抛物曲面的相交 设定了一个圆圈。而 ${\displaystyle \phi }$ 值设定的半平面，切过这圆圈于一个唯一点。这唯一点的直角坐标是^[1]：

${\displaystyle x={\sqrt {\eta \xi }}\ \cos \phi }$ 、

${\displaystyle y={\sqrt {\eta \xi }}\ \sin \phi }$ 、

${\displaystyle z={\frac {1}{2}}(\xi -\eta )}$ 。

参考文献

• Morse PM, Feshbach H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill. 1953: p. 660. ISBN 0-07-043316-X. 引文格式1维护：冗余文本 (link)

• Margenau H, Murphy GM. The Mathematics of Physics and Chemistry. New York: D. van Nostrand. 1956: pp. 185–186. 引文格式1维护：冗余文本 (link)

• Korn GA, Korn TM. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961: p. 180. 引文格式1维护：冗余文本 (link)

• Sauer R, Szabó I. Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. 1967: p. 96. 引文格式1维护：冗余文本 (link)

• Zwillinger D. Handbook of Integration. Boston, MA: Jones and Bartlett. 1992: p. 114. ISBN 0-86720-293-9. 引文格式1维护：冗余文本 (link)

• Moon P, Spencer DE. Parabolic Coordinates (μ, ν, ψ). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd ed., 3rd print ed. New York: Springer-Verlag. 1988: pp. 34–36 (Table 1.08). ISBN 978-0387184302. 引文格式1维护：冗余文本 (link)

1. Menzel, Donald H. Mathematical Physics. United States of America: Dover Publications. 1961: pp. 139. ISBN 978-0486600567 （英语）. 引文格式1维护：冗余文本 (link)