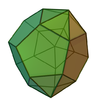
二十四面体

在几何学中，二十四面体是指有24个面的多面体^[3]，在二十四面体当中没有任何一个形状是正多面体，换言之即正二十四面体并不存在，但仍有许多由正多边形组成的二十四面体，例如三侧锥正十二面体（英语：Triaugmented dodecahedron）和五角锥球状屋顶，也有一些接近球状但并非由正多边形组成的二十四面体，其中对称性较高的是三角化八面体和鸢形二十四面体等卡塔兰立体、对称性较低的是部分詹森多面体的对偶多面体，例如双四角帐塔反角柱（英语：Gyroelongated square bicupola）的对偶和异相双四角帐塔柱的对偶。此外要构成二十四面体至少要有14个顶点^[4]。

二十四面体

部分的二十四面体
一种星形二十四面体[1][2]	四角化六面体
伪鸢形二十四面体（英语：Pseudo-deltoidal icositetrahedron）	三侧锥正十二面体

常见的二十四面体

常见的二十四面体中有一些柱体与锥体以及部份的詹森多面体和卡塔兰立体。

二十三角锥

二十三角锥是一种底面为二十三边形的锥体，为二十四面体的一种，具有24个面、46条边和24个顶点，其对偶多面体是自己本身^[5]。正二十三角锥是一种底面为正二十三边形的二十三角锥，在施莱夫利符号中可以用{}∨{23}来表示。底边长为${\displaystyle s}$、高为${\displaystyle h}$的正二十三角锥体积${\displaystyle V}$和表面积${\displaystyle S}$为^[5]：

${\displaystyle V={\frac {23hs^{2}\cot {\frac {\pi }{23}}}{12}}\approx 13.9448hs^{2}}$

${\displaystyle S={\frac {23s\left({\sqrt {4h^{2}+s^{2}\cot ^{2}{\frac {\pi }{23}}}}+s\cot {\frac {\pi }{23}}\right)}{4}}\approx 5.75s\left({\sqrt {4h^{2}+52.9335s^{2}}}+7.27554s\right)}$

二十二角柱

二十二角柱是一种底面为二十二边形的柱体，是二十四面体的一种，由24个面和66条边和44个顶点组成。正二十二角柱代表每个面都是正多边形的二十二角柱，其每个顶点都是2个正方形和1个二十二边形的公共顶点，顶点图以${\displaystyle 4{.}4{.}22}$表示。其在施莱夫利符号中可以用{22}×{}或t{2,22}来表示，在考克斯特符号（英语：Coxeter-Dynkin diagram）中可以用来表示，在威佐夫符号（英语：Wythoff symbol）中可以利用2 22 | 2来表示，在康威多面体表示法中可以利用P22来表示。底边长为${\displaystyle s}$、高为${\displaystyle h}$的正二十二角柱体积${\displaystyle V}$和表面积${\displaystyle S}$为^[6]：

${\displaystyle V={\frac {11hs^{2}\cot {\frac {\pi }{22}}}{2}}\approx 38.2533hs^{2}}$

${\displaystyle S=11s\left(2h+s\cot {\frac {\pi }{22}}\right)\approx 11s\left(2h+6.95515s\right)}$

十一角反棱柱

十一角反棱柱

十一角反棱柱是指底面为十一边形的反棱柱，由24个面、44条边和22个顶点组成。正十一角反棱柱代表每个面都是正多边形的十一角反棱柱，其每个顶点都是3个三角形和1个十一边形的公共顶点，顶点图以3.3.3.11表示。

十二方偏方面体

十二方偏方面体是一种以十二边形为底的偏方面体，由24个全等的鸢形组成，为十二角反角柱的对偶多面体^[7]，同时也是鸢形多面体，是偏方面体系列的第十个成员。所有十二方偏方面体都有24个面、48条边和26个顶点^[7]，其中，顶点有两种，分别为12个鸢形的公共顶点和3个鸢形的公共顶点。

十二方偏方面体是一个等面图形，即面可递多面体，其所有面都相等。更具体来说，其不仅所有面都全等，且面与面必须能在其对称性上传递，也就是说，面必须位于同一个对称性轨道内。这种凸多面体是能做成公正的骰子的形状。^[8]

十二方偏方面体在施莱夫利符号中可以用{ }⨁{12}来表示，在考克斯特符号中可以用或来表示，在康威多面体表示法中可以用dA12来表示。

詹森多面体

在二十四面体中，有2个是詹森多面体，它们分别为：五角锥球状屋顶和三侧锥正十二面体（英语：Triaugmented dodecahedron）。

名称	种类	图像	编号	顶点	边	面	面的种类	对称性	展开图
五角锥球状屋顶	球状屋顶变体		J90	16	38	24	20个正三角形 4个正方形	D2d
三侧锥正十二面体（英语：Triaugmented dodecahedron）	侧锥正多面体		J61	23	45	24	15个正三角形 9个五边形	C3v

卡塔兰立体

主条目：卡塔兰立体

在二十四面体中，有5种拓朴结构明显不同的卡塔兰立体^[9]，分别为三角化八面体、四角化六面体、鸢形二十四面体和五角化二十四面体，其中五角化二十四面体具有2个手性镜像，因此几何上只包含了四种不同的卡塔兰立体。

名称	图像	展开图	对偶	面	边	顶点	顶点布局	点群
三角化八面体	(动画)		截角立方体	24	36	14	等腰三角形 V3.8.8	Oh群
四角化六面体	(动画)		截角八面体	24	36	14	等腰三角形 V4.6.6	Oh群
鸢形二十四面体	(动画)		小斜方截半立方体	24	48	26	鸢形 V3.4.4.4	Oh群
五角二十四面体 (有两种手性镜像)	(动画) (动画)		扭棱立方体	24	60	38	不等边五边形 V3.3.3.3.4	O群

均匀星形多面体

部分的均匀星形多面体也具有24个面：

名称	图像	威佐夫 符号（英语：Wythoff symbol）	顶点图	对称性	C#	W#	U#	K#	顶点	边	面	欧拉	密度（英语：Density_(polytope)）	面种类
双三斜十二面体		3 | 5/3 5	(5/3.5)3	Ih	C53	W080	U41	K46	20	60	24	-16	4	12{5}+12{5/2}
截半大十二面体		3 | 5/3 5	(5/3.5)3	Ih	C53	W080	U41	K46	20	60	24	-16	4	12{5}+12{5/2}
截角大十二面体		2 5/2 | 5	10.10.5/2	Ih	C47	W075	U37	K42	60	90	24	-6	3	12{5/2}+12{10}
小星形截角十二面体		2 5 | 5/3	10/3.10/3.5	Ih	C74	W097	U58	K63	60	90	24	-6	9	12{5}+12{10/3}

二十四面体列表

名称	种类	图像	符号	顶点	边	面	χ	面的种类	对称性	展开图
二十二角柱	棱柱体		t{2,22} {22}x{}	44	66	24	2	2个二十二边形（英语：Icosidigon） 22个矩形	D22h, [22,2], (*22 2 2), order 88
二十三角锥	棱锥体		( )∨{23}	24	46	24	2	1个二十三边形（日语：二十三角形） 23个三角形	C23v, [23], (*23 23)
二十二角锥台	锥台			44	66	24	2	2个二十二边形 22个梯形	D22h, [22,2], (*22 2 2), order 88
双十二角锥	双锥体		{ } + {12}	14	36	24	2	12个三角形	D12h, [12,2], (*2 2 12), order 48
十二方偏方面体	偏方面体		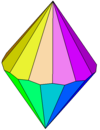{ }⨁{12}[10]:235	26	48	24	2	24个鹞形	D12d, [2+,12], (2*12)
十一角反棱柱	反棱柱		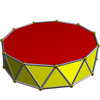s{2,22} sr{2,11}	22	44	24	2	2个十一边形 22个三角形	D11d, [2+,22], (2*11), order 44
十一角帐塔	帐塔			33	55	24	2	11个正三角形 11个正方形 1个正十一边形 1个正二十二边形	D11d, [2+,22], (2*11), 44阶
异相双四角 帐塔柱的对偶 伪鸢形二十四面体[11]	詹森多面体对偶			26	48	24	2	24个鸢形	D4d

参见

• 二十四边形

参考文献

1. Isohedron 24k. loki3.com. [2016-08-29]. （原始内容存档于2019-02-18）. （页面存档备份，存于互联网档案馆）
2. The Isometric Crystal System. metafysica.nl. [2016-08-29]. （原始内容存档于2018-11-29）. （页面存档备份，存于互联网档案馆）
3. Weisstein, Eric W. (编). Icositetrahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
4. Counting polyhedra. numericana.com. [2016-01-10]. （原始内容存档于2020-08-20）. （页面存档备份，存于互联网档案馆）
5. Wolfram, Stephen. "Icositrigonal pyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.
6. Wolfram, Stephen. "Icosidigonal prism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.
7. Wolfram, Stephen. "12-trapezohedron". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.
8. McLean, K. Robin, Dungeons, dragons, and dice, The Mathematical Gazette, 1990, 74 (469): 243–256, JSTOR 3619822, doi:10.2307/3619822.
9. Eugène Catalan Mémoire sur la Théorie des Polyèdres. J. l'École Polytechnique (Paris) 41, 1-71, 1865.
10. Johnson, N.W. Chapter 11: Finite symmetry groups. Geometries and Transformations. 2018. ISBN 978-1-107-10340-5.
11. George Hart. pseudo-rhombicuboctahedra. georgehart.com. [2017-07-22]. （原始内容存档于2012-12-08）. （页面存档备份，存于互联网档案馆）

外部链接

• 埃里克·韦斯坦因. 二十四面體. MathWorld.