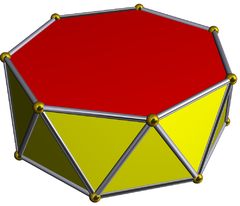
七角反棱柱

在几何学中，七角反棱柱又称为反七角柱或七角反柱是指底为七边形的反棱柱，侧面由三角形组成，若每一个面皆为正多边形则称为正七角反棱柱。每个七角反棱柱皆含有16个面^[1][2][3]，是一种十六面体。

正七角反棱柱

类别	反棱柱 柱状均匀多面体
对偶多面体	七方偏方面体
识别
名称	正七角反棱柱
参考索引	U77(e)
鲍尔斯缩写 （verse-and-dimensions的wikia：Bowers acronym）	heap
数学表示法
考克斯特符号 （英语：Coxeter-Dynkin diagram）
施莱夫利符号	sr{2,7}
威佐夫符号 （英语：Wythoff symbol）	| 2 2 7
康威表示法	A7
性质
面	16
边	28
顶点	14
欧拉特征数	F=16, E=28, V=14 （χ=2）
组成与布局
面的种类	14个三角形 2个正七边形
面的布局 （英语：Face configuration）	14{3}+2{7}
顶点图	3.3.3.7
对称性
对称群	D7d, [2+,14], (2*7), order 28
旋转对称群 （英语：Rotation_groups）	D7, [7,2]+, (722), order 14
特性
凸
图像
3.3.3.7 （顶点图） 七方偏方面体 （对偶多面体）

正七角反棱柱是基底为正七边形的七角反棱柱，其可视为一种半正多面体，施莱夫利符号s{2,7}表示其可以借由七边形二面体透过扭棱变换构造。其具有D₇对称群^[4]，其在威佐夫符号（英语：Wythoff symbol）中用| 2 2 7表示^[5]。

正七角反棱柱

• 
  正七角反棱柱^[6]

当底面为正七边形时，会具备一些特别的性质

当基底边长为a的时候：

• 顶点数目：14^[7]
• 边数目：28
• 面数目：16
• 对偶多面体：七方偏方面体

高：${\displaystyle {\frac {1}{2}}a{\sqrt {4-\sec {\frac {\pi }{14}}\sec {\frac {\pi }{14}}}}}$
表面积：${\displaystyle {\frac {7}{2}}a^{2}(\cot {\frac {\pi }{7}}+{\sqrt {3}})}$
体积：${\displaystyle {\frac {7}{12}}a^{3}(\cot {\frac {\pi }{14}}+\cot {\frac {\pi }{7}}){\sqrt {1-{\frac {1}{4}}\sec {\frac {\pi }{14}}\sec {\frac {\pi }{14}}}}}$

相关多面体与镶嵌

半正七边形二面体球面多面体

对称群（英语：List of spherical symmetry groups）：[7,2], (*722)							[7,2]+, (722)
{7,2}	t{7,2}	r{7,2}	2t{7,2}=t{2,7}	2r{7,2}={2,7}	rr{7,2}	tr{7,2}	sr{7,2}
半正对偶
V72	V142	V72	V4.4.7	V27	V4.4.7	V4.4.14	V3.3.3.7

半正反棱柱系列

2	3	4	5	6	7	8	9	10	11	12	n
s{2,4} sr{2,2}	s{2,6} sr{2,3}	s{2,8} sr{2,4}	s{2,10} sr{2,5}	s{2,12} sr{2,6}	s{2,14} sr{2,7}	s{2,16} sr{2,8}	s{2,18} sr{2,9}	s{2,20} sr{2,10}	s{2,22} sr{2,11}	s{2,24} sr{2,12}	s{2,2n} sr{2,n}
作为球面镶嵌

在其他领域中

参见

• 反棱柱
• 偏方面体